大门|大门-CS-2015（第1组）|问题60

考虑NPDA〈Q={q0，q1，q2}，∑={0，1}，Γ={0，1，⊥}, δ、 问题0，⊥, F={q2}〉, 其中（按照通常惯例）Q是一组状态，∑是输入字母，Γ是堆栈字母，δ是状态转移函数，q0是初始状态，⊥ 是初始堆栈符号，F是接受状态集，状态转换如下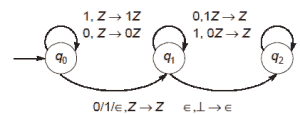： 以下哪一个序列必须跟随字符串101100，以便整个字符串被自动机接受？ （A） 10110 （B） 10010 （C） 01010 （D） 01001 答复: （B） 说明： 在q0状态下，对于“1”，会推送“1”，对于“0”，会推送“0”。在q1状态下，对于“0”弹出“1”，对于“1”弹出“0”。因此，给定的PDA接受所有形式为x0x’r或x1x’r或xx’r的字符串，其中x’r是x的1的补码的倒数。

给定的字符串101100有6个字母，我们有5个字母字符串。x0完成了，x=10110。所以，x’r=（01001）r=10010。

因此，选项B是正确的。

这个问题的小测验