设G(V,E)是一个有n个顶点的有向图。从v到v的路径 我 对v J G是顶点序列(v 我 五、 i+1 , ……., 五、 J )这样(vk,v k+1 )∈E代表i到j-1中的所有k。简单路径是顶点不会出现多次的路径。 假设A是一个nxn数组,初始化如下
null
考虑下面的算法。
for i = 1 to n
for j = 1 to n
for k = 1 to n
A [j , k] = max (A[j, k] (A[j, i] + A [i, k]);
对于上述算法结束后的所有j和k,以下哪项陈述必然正确? (A) A[j,k]≤ N (B) 如果A[j,k]≥ n–1,那么G有一个哈密顿循环 (C) 如果存在从j到k的路径,则[j,k]包含从j到k的最长路径透镜 (D) 如果存在一条从j到k的路径,则从j到k的每条简单路径都包含大多数a[j,k]边 答复: (D) 说明:
In the original input matrix, A[j , k] is 1 if there is an edge from j to k, else 0. Below expression is important to note: A[j , k] = max(A[j, k] (A[j, i] + A [i, k]); This expression puts the count of maximum edges on a path from j to k. In this expression, we consider every vertex k that can become an intermediate vertex and can give longer path.
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
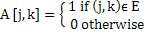


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



