大门|大门-CS-2003 |问题60-yiteyi-C++库

一个程序由两个按顺序执行的模块组成。设f1（t）和f2（t）分别表示执行两个模块所用时间的概率密度函数。执行程序所需总时间的概率密度函数如下所示：

null

         
A) 
B) 
C) 
D)

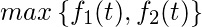
（A） A. （B） B （C） C （D） D 答复: （C） 说明： 我们假设总时间为’t’单位，f1执行’x’单位。因为，f1（t）和f2（t）是顺序执行的。因此，f2是针对‘t–x’单位执行的。我们对两个独立的随机变量之和进行卷积，得到执行程序所需总时间的概率密度函数。 f1（t）*f2（t-x）= $int_{0}^{t}f_{1}(x)f_{2}(t-x)dx$ 因此，选项（C）是正确的。如果你在上面的帖子中发现任何错误，请在下面发表评论。这个问题的小测验

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章