大门|大门-CS-2005 |问题83

设s和t是无向图G+（V，E）中具有不同正边权的两个顶点。设[X，Y]是V的一个划分，使得s&in；X和t&in；考虑在所有具有一个顶点x的边和y中的一个顶点之间具有最小权重的边E。

边e肯定属于： （A） G的最小加权生成树 （B） s到t的加权最短路径 （C） 从s到t的每条路径 （D） 从s到t的加权最长路径 答复: （A） 说明： 任何s-t切割的最小重量边始终是MST的一部分。这叫做 切割特性 .

这就是我们的想法 普里姆算法 .最小权割边始终是最小生成树边。

为什么B（从s到t的加权最短路径）不是答案？ 参见下面的示例，边4（从s到t的高亮红色切割中最亮的部分）不是最短路径的一部分。 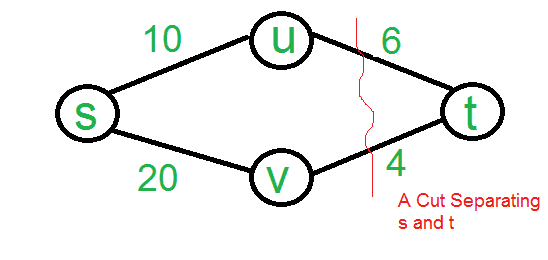这个问题的小测验