如果矩阵A是这样的
null
那么A的行列式等于 (A) 0 (B) 1. (C) 2. (D) 3. 答复: (A) 说明: 这是门纸的数字回答问题,没有提供选项,答案是在提供的文本框中填入数字。
在这个问题中,矩阵A是两个矩阵的乘积,这两个矩阵的阶数分别为3×1和1×3。在这些矩阵相乘之后,矩阵A将是一个3×3阶的方阵。
矩阵A是:
2 18 10 -4 -36 -20 7 63 35
现在,我们可以通过观察矩阵来观察,通过使用第1行,第2行可以完全为零,这是通过使用矩阵的行运算来实现的,这里是:
R2
在矩阵中应用上述行操作后,生成的矩阵将是:
2 18 10 0 0 0 7 63 35
i、 e.第二排现在变成了零。如果一个方阵的行或列的所有元素都是0,那么它的行列式是0。(方阵的一个性质)
所以答案是0。
注:行列式仅适用于方阵,它是一个编码矩阵某些属性的数字,例如:行列式为0的方阵没有其逆矩阵。 这个问题的小测验
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
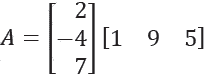


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



