门|门CS 2012 |问题11

设A为2×2矩阵，元素a11=a12=a21=+1和a22=−1.然后矩阵A的特征值 ¹⁹ 是

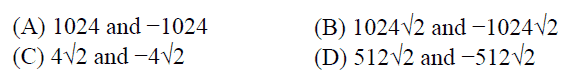（A） A. （B） B （C） C （D） D 答复: （D） 说明：

A =  1    1
     1   -1

A2 = 2   0
                0   2

A4 = A2 X A2
A4 = 4   0
                0   4

A8 = 16   0
                0    16


A16 = 256   0
                 0    256

A18 = A16 X A2
A18 = 512   0
                 0    512 

A19 = 512   512
                 512  -512


Applying Characteristic polynomial

512-lambda   512
512       -(512+lambda)  =   0

-(512-lambda)(512+lambda) - 512 x 512 = 0

lambda2 = 2 x 5122 

替代解决方案：

det(A) = -2.
det(A^19) = (det(A))^19 = -2^19 = lambda1*lambda2.
The only viable option is D. 

感谢Matan Mandelbrod提出了这个解决方案。

这个问题的小测验