大门| 2012年CS大门|问题5

在包含n2^n个元素的二元搜索树中，在平衡的搜索树中搜索元素的最坏情况下运行时间为

(A) 

(B) 

(C) 

(D)  

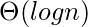
（A） A. （B） B （C） C （D） D 答复: （C） 说明：

->二叉搜索树中的搜索时间取决于树的形式，即其节点的插入顺序。病理病例：n个节点通过增加键的顺序插入，产生类似于线性列表的结果（但空间消耗更大），搜索时间为O（n）（在斜树的情况下）。

->平衡树是指每一片叶子与根部的距离不超过某一距离的树。所以在平衡树中，树的高度是平衡的，以使根和叶节点之间的距离尽可能小。在平衡树中，树的高度是圆木 _2. （n） 。

->因此，如果平衡二叉搜索树包含n2n元素，则搜索项目的时间复杂度为：

时间复杂度=对数（n2 ^N )=log（n）+log（2） ^N ) =log（n）+n=O（n）

所以答案是C。

看见 https://www.geeksforgeeks.org/data-structures-and-algorithms-set-28/

这个解决方案是由 尼马尔·巴拉德瓦伊 这个问题的小测验