考虑以下功能:
null
int unknown( int n) { int i, j, k = 0; for (i = n/2; i <= n; i++) for (j = 2; j <= n; j = j * 2) k = k + n/2; return k; } |
(A)
![]()
(B)
![]()
(C)
![]()
(D)
![]()
(A) A. (B) B (C) C (D) D 答复: (B) 说明: 在这里,我们必须告诉k返回的值,而不是时间复杂度。
for (i = n/2; i <= n; i++) for (j = 2; j <= n; j = j * 2) k = k + n/2; return k;
外部循环运行n/2次 内部循环运行logn次。(2^k=n=>k=logn)。 现在看看内循环中k的值,n被加到k,logn次,因为内循环运行logn次。 因此,总时间复杂度是内环乘以外环复杂度,即(n表示外环,nlogn表示内环)n*logn。
因此,运行内部循环一次后的k值为n^2logn。 看见 http://geeksquiz.com/algorithms-analysis-of-algorithms-question-5/ 这个解决方案是由 帕鲁尔·夏尔马。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
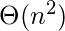


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



