GATE | GATE-IT-2004 |问题56

考虑下面的无向图：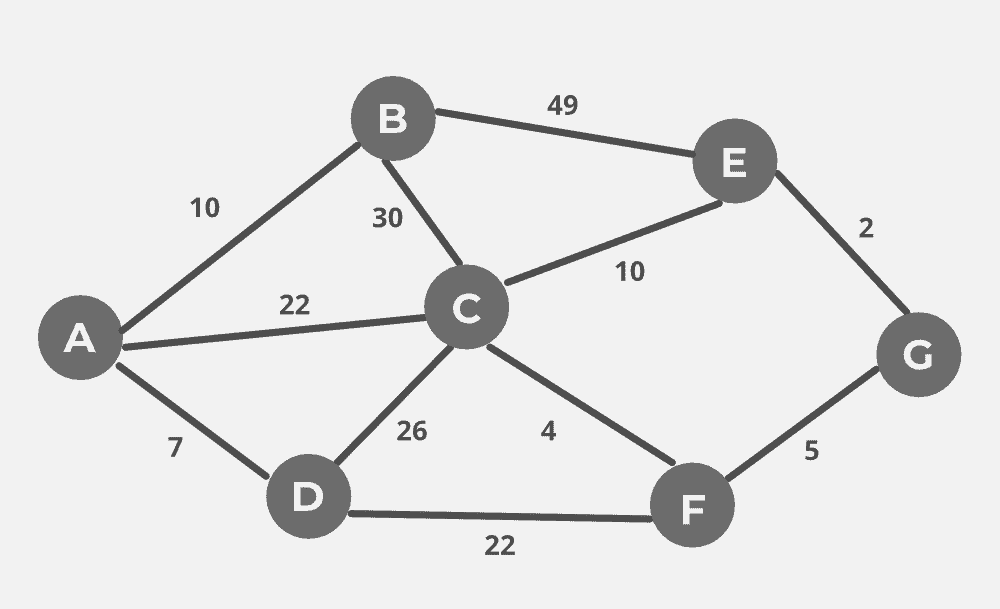

使用Prim的算法从节点a开始构造最小生成树，以下哪一条边序列代表了将边添加到构造最小生成树的可能顺序？ （A） （E，G），（C，F），（F，G），（A，D），（A，B），（A，C） （B） （A，D）、（A，B）、（A，C）、（C，F）、（G，E）、（F，G） （C） （A，B），（A，D），（D，F），（F，G），（G，E），（F，C） （D） （A，D）、（A，B）、（D，F）、（F，C）、（F，G）、（G，E）

答复: （D） 说明： A. 错误的 Prim算法背后的思想是构造一棵生成树—— 意味着所有顶点都必须连接 但这里的顶点是断开的

B 错误的 Prim算法背后的思想是构造一棵生成树—— 意味着所有顶点都必须连接 但这里的顶点是断开的

C 错误的 Prim’s是一家 贪婪算法 在每一步中，它都会考虑连接两个集合的所有边，并从这些边中选取最小权重边。在该选项中，必须首先拾取AB

D 符合事实的

因此，答案是D

普里姆的算法也是一个很好的例子 贪婪算法 .它从一个空的生成树开始。 其思想是保持两组顶点。第一个集合包含MST中已包含的顶点，另一个集合包含尚未包含的顶点。在每一步中，它都会考虑连接两个集合的所有边，并从这些边中选取最小权重边。拾取边后，它会将边的另一个端点移动到包含MST的集合。

更多信息请访问：https://www.geeksforgeeks.org/greedy-algorithms-set-5-prims-minimum-spanning-tree-mst-2/ 这个问题的小测验 如果你在上面的帖子中发现任何错误，请在下面发表评论