如果为每个节点分配了标签,则二叉树被标记;如果未为节点分配任何标签,则二叉树被取消标记。
null
Below two are considered same unlabelled trees o o / / o o o o Below two are considered different labelled trees A C / / B C A B
有n个节点可以有多少不同的未标记二叉树?
For n = 1, there is only one tree oFor n = 2, there are two trees o o / o oFor n = 3, there are five trees o o o o o / / / o o o o o o / /o o o o
其思想是考虑左、右子树中节点的所有可能计数对,并乘以特定对的计数。最后,将所有对的结果相加。
For example, let T(n) be count for n nodes.T(0) = 1 [There is only 1 empty tree]T(1) = 1T(2) = 2T(3) = T(0)*T(2) + T(1)*T(1) + T(2)*T(0) = 1*2 + 1*1 + 2*1 = 5T(4) = T(0)*T(3) + T(1)*T(2) + T(2)*T(1) + T(3)*T(0) = 1*5 + 1*2 + 2*1 + 5*1 = 14
上述模式基本上代表了 加泰罗尼亚数字 前几个加泰罗尼亚人的数字是1 1 2 5 14 42 132 429 1430 4862,… ![]() 在这里 T(i-1)表示左子树上的节点数 T(n)−i-1)表示右子树上的节点数
在这里 T(i-1)表示左子树上的节点数 T(n)−i-1)表示右子树上的节点数
n’th Catalan数也可以用直接公式计算。
T(n) = (2n)! / (n+1)!n!
具有n个节点的二叉搜索树(BST)的数量也与未标记树的数量相同。原因很简单,在BST中,我们也可以将任何键设为根,如果根是按排序顺序排列的第i个键,那么i-1键可以位于一侧,而(n-i)键可以位于另一侧。
有n个节点可以有多少标记的二叉树? 要计算标记树的数量,我们可以使用上面的计数来计算未标记树的数量。这个想法很简单,每个有n个节点的未标记树都可以创建n个!通过将不同的标签排列分配给所有节点,可以获得不同的标签树。
因此
Number of Labelled Trees = (Number of unlabelled trees) * n! = [(2n)! / (n+1)!n!] × n!
例如,对于n=3,有5*3!=5*6=30棵不同的树
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
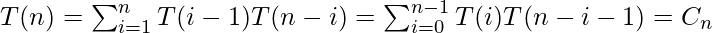


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



