谜题9 |（找出最快的3匹马）

有25匹马，其中你需要找出最快的3匹马。你最多可以在5人之间进行比赛，以了解他们的相对速度。在任何情况下，你都无法了解赛马的实际速度。找出获得前三名所需的最少比赛次数。

答案是7。

首先，我们把马分成5组，每组在赛马场上比赛。这给了我们5场比赛（见下图）。

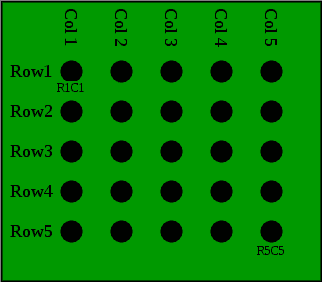
在图中，每行代表一个5匹马的比赛。为了方便起见，让我们使用行和列索引来命名这些马。因此，第一场比赛（第一排）是在R1C1、R1C2、R1C3、R1C4和R1C5之间进行的。第二场比赛（第2排）是R2C1、R2C2等马之间的较量。让我们假设每排的第五名成员赢得了比赛（R1C5赢得了第一场比赛，R2C5赢得了第二场比赛，依此类推），每排的第四名选手获得第二名（R1C4在第一场比赛中获得第二名，R2C4在第二场比赛中获得第二名，依此类推），每组的第三名选手获得第三名（R1C3在第一场比赛中获得第三名，R2C3在第二场比赛中获得第三名，依此类推）。

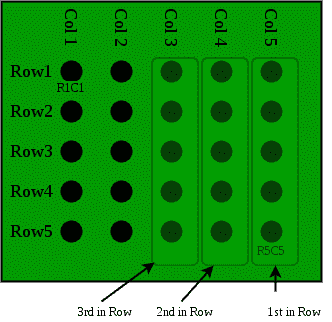
接下来，我们将与5名一级优胜者（R1C5、R2C5、R3C5、R4C5和R5C5）比赛。假设R1C5赢得这场比赛，R2C5排名第二，R3C5排名第三。

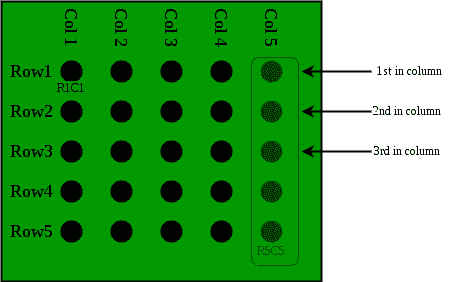
这场比赛的获胜者（R1C5）是整个组中跑得最快的马。现在，在整个组中排名第二的马可以是R2C5或R1C4。在整个组别中排名第三的马可以是R3C5、R2C4或R1C3。因此，我们比赛这5匹马。

因此，马R1C5是最快的马。在最后一场比赛中排名第一和第二的马分别是在整个组中排名第二和第三的马。这样，确定整个组别中第一、第二和第三匹马所需的最小比赛次数为7。 这一解释由 费罗斯·拜格

另一种解释：

5匹马一组，跑5场比赛。假设五组是a、b、c、d、e，下一个字母表是它在这组中的个人等级（共5匹马）。d3代表d组中的马，在他的组中排名第三。[5场比赛结束] a1 b1 c1 d1 e1 a2 b2 c2 d2 e2 a3 b3 c3 d3 e3 a4 b4 c4 d4 e4 a5 b5 c5 d5 e5

现在做一个（a1，b1，c1，d1，e1）的比赛。[RACE 6 DONE]假设结果为a1>b1>c1>d1>e1 这意味着a1必须是第一位。 b1和c1可以是（但不是必须是）第二和第三。 对于II位置，马将是b1或a2 （我们必须找到前三名的马，因此我们选择b1、b2、a2、a3、c1等马进行比赛[RACE 7 DONE]。 唯一的可能性是： c1可能是第三位 b1可以是第二个或第三个 b2可能是第三位 a2可以是第二个或第三个 a3可能是第三名 最终结果将给出答案。假设结果是a2>a3>b1>c1>b2 然后答案是a1，a2，a3，b1，c1。 所以答案是7场比赛

请注意，当所有前三名的马都是同一组或任何前两名的马都是同一组时，这7场比赛也适用。第六组的冠军总是有三匹。在第七场比赛中，我们认为第二匹和第三匹马的马是整体冠军。我们还考虑了第二匹马，在第六场比赛中，马的数量是第二匹。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论