求三角形面积的程序-yiteyi-C++库

使用给定边查找区域：

null

例如：

Input : a = 5, b = 7, c = 8Output : Area of a triangle is 17.320508Input : a = 3, b = 4, c = 5Output : Area of a triangle is 6.000000

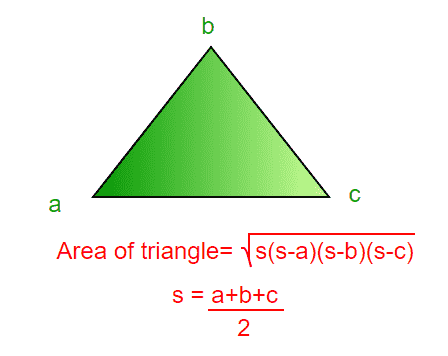
面积三角形可以简单地用以下公式计算。

Area = sqrt(s*(s-a)*(s-b)*(s-c))where a, b and c are lengths of sides oftriangle and s = (a+b+c)/2

Program to find area of a triangle

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

C++

                         // C++ Program to find the area                       
                         // of triangle                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         float                                     findArea(                                     float                                     a,                                     float                                     b,                                     float                                     c)                       
                         {                       
                                                 // Length of sides must be positive                       
                                                 // and sum of any two sides                       
                                                 // must be smaller than third side.                       
                                                 if                                     (a < 0 || b < 0 || c < 0 ||                       
                                                 (a + b <= c) || a + c <= b ||                       
                                                 b + c <= a)                       
                                                 {                       
                                                 cout <<                                     "Not a valid triangle"                                     ;                       
                                                 exit                                     (0);                       
                                                 }                       
                                                 float                                     s = (a + b + c) / 2;                       
                                                 return                                     sqrt                                     (s * (s - a) *                       
                                                 (s - b) * (s - c));                       
                         }                       
           
                         // Driver Code                       
                         int                                     main()                       
                         {                       
                                                 float                                     a = 3.0;                       
                                                 float                                     b = 4.0;                       
                                                 float                                     c = 5.0;                       
           
                                                 cout <<                                     "Area is "                                     << findArea(a, b, c);                       
                                                 return                                     0;                       
                         }                       
           
                         // This code is contributed                       
                         // by rathbhupendra                       

C

                         #include <stdio.h>                       
                         #include <stdlib.h>                       
           
                         float                                     findArea(                                     float                                     a,                                     float                                     b,                                     float                                     c)                       
                         {                       
                                                 // Length of sides must be positive and sum of any two sides                       
                                                 // must be smaller than third side.                       
                                                 if                                     (a < 0 || b < 0 || c <0 || (a+b <= c) ||                       
                                                 a+c <=b || b+c <=a)                       
                                                 {                       
                                                 printf                                     (                                     "Not a valid triangle"                                     );                       
                                                 exit                                     (0);                       
                                                 }                       
                                                 float                                     s = (a+b+c)/2;                       
                                                 return                                     sqrt                                     (s*(s-a)*(s-b)*(s-c));                       
                         }                       
           
                         int                                     main()                       
                         {                       
                                                 float                                     a = 3.0;                       
                                                 float                                     b = 4.0;                       
                                                 float                                     c = 5.0;                       
           
                                                 printf                                     (                                     "Area is %f"                                     , findArea(a, b, c));                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to print                       
                         // Floyd's triangle                       
                                   
                         class                                     Test                       
                         {                       
                                                 static                                     float                                     findArea(                                     float                                     a,                                     float                                     b,                                     float                                     c)                       
                                                 {                       
                                                 // Length of sides must be positive and sum of any two sides                       
                                                 // must be smaller than third side.                       
                                                 if                                     (a <                                     0                                     || b <                                     0                                     || c <                                     0                                     || (a+b <= c) ||                       
                                                 a+c <=b || b+c <=a)                       
                                                 {                       
                                                 System.out.println(                                     "Not a valid triangle"                                     );                       
                                                 System.exit(                                     0                                     );                       
                                                 }                       
                                                 float                                     s = (a+b+c)/                                     2                                     ;                       
                                                 return                                     (                                     float                                     )Math.sqrt(s*(s-a)*(s-b)*(s-c));                       
                                                 }                       
                                   
                                                 // Driver method                       
                                                 public                                     static                                     void                                     main(String[] args)                       
                                                 {                       
                                                 float                                     a =                                     3                                     .0f;                       
                                                 float                                     b =                                     4                                     .0f;                       
                                                 float                                     c =                                     5                                     .0f;                       
                                   
                                                 System.out.println(                                     "Area is "                                     + findArea(a, b, c));                       
                                                 }                       
                         }                       

Python3

                         # Python Program to find the area                       
                         # of triangle                       
           
                         # Length of sides must be positive                       
                         # and sum of any two sides                       
                         def                                     findArea(a,b,c):                       
           
                                                 # must be smaller than third side.                       
                                                 if                                     (a <                                     0                                     or                                     b <                                     0                                     or                                     c <                                     0                                     or                                     (a                                     +                                     b <                                     =                                     c)                                     or                                     (a                                     +                                     c <                                     =                                     b)                                     or                                     (b                                     +                                     c <                                     =                                     a) ):                       
                                                 print                                     (                                     'Not a valid triangle'                                     )                       
                                                 return                       
                                   
                                                 # calculate the semi-perimeter                       
                                                 s                                     =                                     (a                                     +                                     b                                     +                                     c)                                     /                                     2                       
                                   
                                                 # calculate the area                       
                                                 area                                     =                                     (s                                     *                                     (s                                     -                                     a)                                     *                                     (s                                     -                                     b)                                     *                                     (s                                     -                                     c))                                     *                                     *                                     0.5                       
                                                 print                                     (                                     'Area of a triangle is %f'                                     %                                     area)                       
           
           
                         # Initialize first side of triangle                       
                         a                                     =                                     3.0                       
                         # Initialize second side of triangle                       
                         b                                     =                                     4.0                       
                         # Initialize Third side of triangle                       
                         c                                     =                                     5.0                       
                         findArea(a,b,c)                       
           
                         # This code is contributed by Shariq Raza                       

C#

                         // C# program to print                       
                         // Floyd's triangle                       
                         using                                     System;                       
           
                         class                                     Test {                       
                                   
                                                 // Function to find area                       
                                                 static                                     float                                     findArea(                                     float                                     a,                                     float                                     b,                       
                                                 float                                     c)                       
                                                 {                       
                                   
                                                 // Length of sides must be positive                       
                                                 // and sum of any two sides                       
                                                 // must be smaller than third side.                       
                                                 if                                     (a < 0 || b < 0 || c <0 ||                       
                                                 (a + b <= c) || a + c <=b ||                       
                                                 b + c <=a)                       
                                                 {                       
                                                 Console.Write(                                     "Not a valid triangle"                                     );                       
                                                 System.Environment.Exit(0);                       
                                                 }                       
                                                 float                                     s = (a + b + c) / 2;                       
                                                 return                                     (                                     float                                     )Math.Sqrt(s * (s - a) *                       
                                                 (s - b) * (s - c));                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 public                                     static                                     void                                     Main()                       
                                                 {                       
                                                 float                                     a = 3.0f;                       
                                                 float                                     b = 4.0f;                       
                                                 float                                     c = 5.0f;                       
                                   
                                                 Console.Write(                                     "Area is "                                     + findArea(a, b, c));                       
                                                 }                       
                         }                       
           
                         // This code is contributed Nitin Mittal.                       

PHP

                         <?php                       
                         function                                     findArea(                                     $a                                     ,                                     $b                                     ,                                     $c                                     )                       
                         {                       
                                                 // Length of sides must be positive                       
                                                 // and sum of any two sides must                       
                                                 // be smaller than third side.                       
                                                 if                                     (                                     $a                                     < 0                                     or                                     $b                                     < 0                                     or                       
                                                 $c                                     < 0                                     or                                     (                                     $a                                     +                                     $b                                     <=                                     $c                                     )                                     or                       
                                                 $a                                     +                                     $c                                     <=                                     $b                                     or                                     $b                                     +                                     $c                                     <=                                     $a                                     )                       
                                                 {                       
                                                 echo                                     "Not a valid triangle"                                     ;                       
                                                 exit                                     (0);                       
                                                 }                       
                                                 $s                                     = (                                     $a                                     +                                     $b                                     +                                     $c                                     ) / 2;                       
                                                 return                                     sqrt(                                     $s                                     * (                                     $s                                     -                                     $a                                     ) *                       
                                                 (                                     $s                                     -                                     $b                                     ) * (                                     $s                                     -                                     $c                                     ));                       
                         }                       
           
                         // Driver Code                       
                         $a                                     = 3.0;                       
                         $b                                     = 4.0;                       
                         $c                                     = 5.0;                       
           
                         echo                                     "Area is "                                     , findArea(                                     $a                                     ,                                     $b                                     ,                                     $c                                     );                       
           
                         // This code is contributed anuJ_67.                       
                         ?>                       

Javascript

                         <script>                       
           
                         // javascript Program to find the area                       
                         // of triangle                       
           
                         function                                     findArea( a,  b,  c)                       
                         {                       
                                                 // Length of sides must be positive                       
                                                 // and sum of any two sides                       
                                                 // must be smaller than third side.                       
                                                 if                                     (a < 0 || b < 0 || c < 0 ||                       
                                                 (a + b <= c) || a + c <= b ||                       
                                                 b + c <= a)                       
                                                 {                       
                                                 document.write(                                     "Not a valid triangle"                                     );                       
                                                 return                                     ;                       
                                                 }                       
                                                 let s = (a + b + c) / 2;                       
                                                 return                                     Math.sqrt(s * (s - a) *                       
                                                 (s - b) * (s - c));                       
                         }                       
           
                         // Driver Code                       
           
                                                 let a = 3.0;                       
                                                 let b = 4.0;                       
                                                 let c = 5.0;                       
           
                                                 document.write(                                     "Area is "                                     + findArea(a, b, c));                       
           
                         // This code is contributed by todaysgaurav                       
           
                         </script>                       

输出：

Area is 6

时间复杂性： O（原木） _2. n）

辅助空间： O（1） 使用坐标查找区域：

如果给我们三个角的坐标，我们可以在下面应用鞋带配方对于区域。

Area= | 1/2 [ (x₁y₂ + x₂y₃ + ... + x_n-1y_n + x_ny₁) -(x₂y₁ + x₃y₂ + ... + x_ny_n-1 + x₁y_n) ] |

C++

                         // C++ program to evaluate area of a polygon using                       
                         // shoelace formula                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
                                   
                         // (X[i], Y[i]) are coordinates of i'th point.                       
                         double                                     polygonArea(                                     double                                     X[],                                     double                                     Y[],                                     int                                     n)                       
                         {                       
                                                 // Initialize area                       
                                                 double                                     area = 0.0;                       
                                   
                                                 // Calculate value of shoelace formula                       
                                                 int                                     j = n - 1;                       
                                                 for                                     (                                     int                                     i = 0; i < n; i++)                       
                                                 {                       
                                                 area += (X[j] + X[i]) * (Y[j] - Y[i]);                       
                                                 j = i;                                     // j is previous vertex to i                       
                                                 }                       
                                   
                                                 // Return absolute value                       
                                                 return                                     abs                                     (area / 2.0);                       
                         }                       
                                   
                         // Driver program to test above function                       
                         int                                     main()                       
                         {                       
                                                 double                                     X[] = {0, 2, 4};                       
                                                 double                                     Y[] = {1, 3, 7};                       
                                   
                                                 int                                     n =                                     sizeof                                     (X)/                                     sizeof                                     (X[0]);                       
                                   
                                                 cout << polygonArea(X, Y, n);                       
                         }                       

JAVA

                         // Java program to evaluate area of                       
                         // a polygon usingshoelace formula                       
                         import                                     java.io.*;                       
                         import                                     java.math.*;                       
           
                         class                                     GFG {                       
           
                                                 // (X[i], Y[i]) are coordinates of i'th point.                       
                                                 static                                     double                                     polygonArea(                                     double                                     X[],                                     double                                     Y[],                                     int                                     n)                       
                                                 {                       
                                                 // Initialize area                       
                                                 double                                     area =                                     0.0                                     ;                       
                                   
                                                 // Calculate value of shoelace formula                       
                                                 int                                     j = n -                                     1                                     ;                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < n; i++)                       
                                                 {                       
                                                 area += (X[j] + X[i]) * (Y[j] - Y[i]);                       
                                   
                                                 // j is previous vertex to i                       
                                                 j = i;                       
                                                 }                       
                                   
                                                 // Return absolute value                       
                                                 return                                     Math.abs(area /                                     2.0                                     );                       
                                                 }                       
                                   
                                                 // Driver program                       
                                                 public                                     static                                     void                                     main (String[] args)                       
                                                 {                       
                                                 double                                     X[] = {                                     0                                     ,                                     2                                     ,                                     4                                     };                       
                                                 double                                     Y[] = {                                     1                                     ,                                     3                                     ,                                     7                                     };                       
           
                                                 int                                     n = X.length;                       
                                                 System.out.println(polygonArea(X, Y, n));                       
                                                 }                       
                         }                       
           
           
                         // This code is contributed                       
                         // by Nikita Tiwari.                       

Python3

                         # Python 3 program to evaluate                       
                         # area of a polygon using                       
                         # shoelace formula                       
           
                         # (X[i], Y[i]) are coordinates of i'th point.                       
                         def                                     polygonArea(X,Y, n) :                       
           
                                                 # Initialize area                       
                                                 area                                     =                                     0.0                       
                                   
                                                 # Calculate value of shoelace formula                       
                                                 j                                     =                                     n                                     -                                     1                       
                                                 for                                     i                                     in                                     range                                     (                                     0                                     , n) :                       
                                                 area                                     =                                     area                                     +                                     (X[j]                                     +                                     X[i])                                     *                                     (Y[j]                                     -                                     Y[i])                       
                                                 j                                     =                                     i                                     # j is previous vertex to i                       
                                   
                                   
                                                 # Return absolute value                       
                                                 return                                     abs                                     (area                                     /                                     /                                     2.0                                     )                       
           
                                   
                         # Driver program to test above function                       
                         X                                     =                                     [                                     0                                     ,                                     2                                     ,                                     4                                     ]                       
                         Y                                     =                                     [                                     1                                     ,                                     3                                     ,                                     7                                     ]                       
           
                         n                                     =                                     len                                     (X)                       
                         print                                     (polygonArea(X, Y, n))                       
           
           
                         # This code is contributed                       
                         # by Nikita Tiwari.                       

C#

                         // C# program to evaluate area of                       
                         // a polygon usingshoelace formula                       
                         using                                     System;                       
           
                         class                                     GFG {                       
           
                                                 // (X[i], Y[i]) are coordinates                       
                                                 // of i'th point.                       
                                                 static                                     double                                     polygonArea(                                     double                                     []X,                       
                                                 double                                     []Y,                                     int                                     n)                       
                                                 {                       
                                                 // Initialize area                       
                                                 double                                     area = 0.0;                       
                                   
                                                 // Calculate value of shoelace                       
                                                 // formula                       
                                                 int                                     j = n - 1;                       
                                                 for                                     (                                     int                                     i = 0; i < n; i++)                       
                                                 {                       
                                                 area += (X[j] + X[i]) *                       
                                                 (Y[j] - Y[i]);                       
                                   
                                                 // j is previous vertex to i                       
                                                 j = i;                       
                                                 }                       
                                   
                                                 // Return absolute value                       
                                                 return                                     Math.Abs(area / 2.0);                       
                                                 }                       
                                   
                                                 // Driver program                       
                                                 public                                     static                                     void                                     Main ()                       
                                                 {                       
                                                 double                                     []X = {0, 2, 4};                       
                                                 double                                     []Y = {1, 3, 7};                       
           
                                                 int                                     n = X.Length;                       
                                                 Console.WriteLine(                       
                                                 polygonArea(X, Y, n));                       
                                                 }                       
                         }                       
           
                         // This code is contributed by anuj_67.                       

PHP

                         <?php                       
                         // PHP program to evaluate area of a                       
                         // polygon using shoelace formula                       
           
                         // (X[i], Y[i]) are coordinates                       
                         // of i'th point.                       
                         function                                     polygonArea(                                     $X                                     ,                                     $Y                                     ,                                     $n                                     )                       
                         {                       
                                   
                                                 // Initialize area                       
                                                 $area                                     = 0.0;                       
           
                                                 // Calculate value of                       
                                                 // shoelace formula                       
                                                 $j                                     =                                     $n                                     - 1;                       
                                                 for                                     (                                     $i                                     = 0;                                     $i                                     <                                     $n                                     ;                                     $i                                     ++)                       
                                                 {                       
                                                 $area                                     += (                                     $X                                     [                                     $j                                     ] +                                     $X                                     [                                     $i                                     ]) *                       
                                                 (                                     $Y                                     [                                     $j                                     ] -                                     $Y                                     [                                     $i                                     ]);                       
                                   
                                                 // j is previous vertex to i                       
                                                 $j                                     =                                     $i                                     ;                       
                                                 }                       
           
                                                 // Return absolute value                       
                                                 return                                     abs                                     (                                     $area                                     / 2.0);                       
                         }                       
           
                                                 // Driver Code                       
                                                 $X                                     =                                     array                                     (0, 2, 4);                       
                                                 $Y                                     =                                     array                                     (1, 3, 7);                       
                                                 $n                                     =                                     count                                     (                                     $X                                     );                       
                                                 echo                                     polygonArea(                                     $X                                     ,                                     $Y                                     ,                                     $n                                     );                       
           
                         // This code is contributed by anuj_67.                       
                         ?>                       

Javascript

                         <script>                       
           
                         // Javascript program to evaluate area of a polygon using                       
                         // shoelace formula                       
           
                         // (X[i], Y[i]) are coordinates of i'th point.                       
                         function                                     polygonArea(X, Y, n)                       
                         {                       
           
                                                 // Initialize area                       
                                                 let area = 0.0;                       
           
                                                 // Calculate value of shoelace formula                       
                                                 let j = n - 1;                       
                                                 for                                     (let i = 0; i < n; i++)                       
                                                 {                       
                                                 area += (X[j] + X[i]) * (Y[j] - Y[i]);                       
                                                 j = i;                                     // j is previous vertex to i                       
                                                 }                       
           
                                                 // Return absolute value                       
                                                 return                                     Math.abs(area / 2.0);                       
                         }                       
           
                         // Driver program to test above function                       
                                                 let X = [0, 2, 4];                       
                                                 let Y = [1, 3, 7];                       
           
                                                 let n = X.length;                       
           
                                                 document.write(polygonArea(X, Y, n));                       
           
                         // This code is contributed by Mayank Tyagi                       
           
                         </script>                       

输出：

时间复杂性： O（n）

辅助空间： O（1）

https://www.youtube.com/watch?v=-fuEL8MEtOc

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章