DFA的最小化

DFA最小化是指将给定的DFA转换为具有最少状态数的等效DFA。

DFA的最小化 假设存在识别语言L的DFA D ，则语言L的最小化DFA D 可构造为： 第一步： 我们将Q（状态集）分成两组。一组包含所有最终状态，另一组包含非最终状态。这个分区叫做P ₀ . 第二步： 初始化k=1 第三步： 找到P _K 通过划分不同的P _k-1 .在每一组P _k-1 ，我们将采取所有可能的成对状态。如果一个集合的两个状态是可区分的，我们将在P中把集合分成不同的集合 _K . 第4步： 当P _K =P _k-1 （分区无变化） 第5步： 一个集合的所有状态都合并为一个集合。最小化DFA中的状态数将等于P中的集合数 _K .

如何找到分区P中的两个状态 _K 它们是可分辨的吗？ 两种状态（qi，qj）在分区P中是可区分的 _K 如果对于任何输入符号a，δ（qi，a）和δ（qj，a）在分区P中处于不同的集合中 _k-1 . 实例 考虑下面的DFA，如图所示。

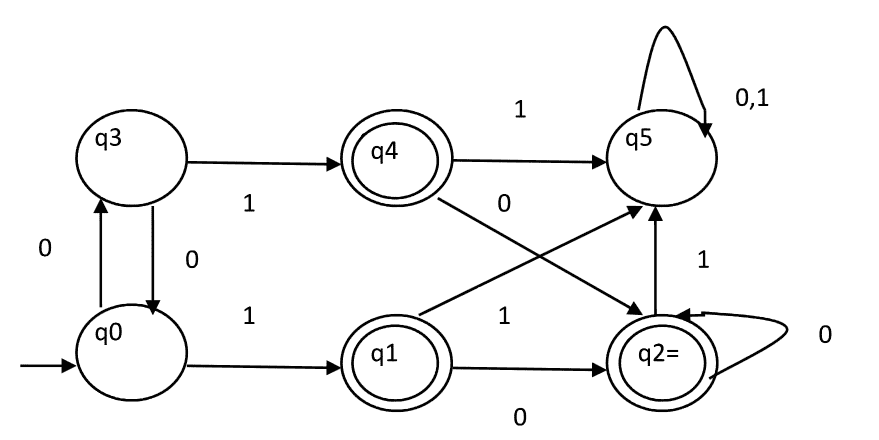
第一步。 P0将有两组状态。一组将包含DFA的最终状态q1、q2、q4，另一组将包含剩余状态。所以P0={q1，q2，q4}，{q0，q3，q5}。 第二步。 为了计算P1，我们将检查分区P0的集合是否可以被分区：

i） 对于集合{q1，q2，q4}： δ（q1，0）=δ（q2，0）=q2和δ（q1，1）=δ（q2，1）=q5，因此q1和q2是不可区分的。 类似地，δ（q1，0）=δ（q4，0）=q2和δ（q1，1）=δ（q4，1）=q5，因此q1和q4是不可区分的。 因为q1和q2是不可区分的，而q1和q4也是不可区分的，所以q2和q4是不可区分的。所以，{q1，q2，q4}集不会在P1中被划分。

ii）对于集合{q0，q3，q5}： δ（q0，0）=q3和δ（q3，0）=q0 δ（q0，1）=q1和δ（q3，1）=q4 q0和q3在输入符号0上的移动分别是q3和q0，它们在分区P0的同一集中。类似地，q0和q3在输入符号1上的移动是分区P0中相同集合中的q3和q0。所以，q0和q3是不可区分的。

δ（q0，0）=q3和δ（q5，0）=q5和δ（q0，1）=q1和δ（q5，1）=q5 q0和q5在输入符号1上的移动分别是q1和q5，它们在分区P0的不同集合中。所以，q0和q5是可以区分的。所以，集合{q0，q3，q5}将被划分为{q0，q3}和{q5}。所以 P1={q1，q2，q4}，{q0，q3}，{q5}

为了计算P2，我们将检查分区P1的集合是否可以被分区： iii）对于集合{q1，q2，q4}： δ（q1，0）=δ（q2，0）=q2和δ（q1，1）=δ（q2，1）=q5，因此q1和q2是不可区分的。 类似地，δ（q1，0）=δ（q4，0）=q2和δ（q1，1）=δ（q4，1）=q5，因此q1和q4是不可区分的。 因为q1和q2是不可区分的，而q1和q4也是不可区分的，所以q2和q4是不可区分的。所以，{q1，q2，q4}集不会在P2中被划分。

iv）对于集合{q0，q3}： δ（q0，0）=q3和δ（q3，0）=q0 δ（q0，1）=q1和δ（q3，1）=q4 q0和q3在输入符号0上的移动分别是q3和q0，它们在分区P1的同一集中。类似地，输入符号1上q0和q3的移动是分区P1中相同集合中的q3和q0。所以，q0和q3是不可区分的。

v） 对于集合{q5}： 因为在这个集合中只有一个状态，所以不能进一步划分。所以 P2={q1，q2，q4}，{q0，q3}，{q5} 因为P1=P2。这是最后一个分区。分区P2意味着q1、q2和q4状态合并为一个。类似地，q0和q3合并为一个。图1的DFA对应的最小化DFA如图2所示：

问题: 考虑给定的DFA。以下哪项是错误的？ 1.L（A）的补语是上下文无关的。 2.L（A）=L（（11*0+0）（0+1）*0*1*） 3.对于A所接受的语言，A是最小的DFA。 4.A接受长度至少为2的{0，1}以上的所有字符串。

A.仅限1和3 B.仅限2和4 C.仅限第2条和第3条 D.仅限3和4

解决方案： 声明4表示，它将接受长度至少为2的所有字符串。但它接受长度为1的0。所以，4是假的。 声明3说，DFA是最小的。我们将使用上面讨论的算法进行检查。 P0={q2}，{q0，q1} P1={q2}，{q0，q1}。因为，P0=P1，P1是最终的DFA。q0和q1可以合并。所以最小DFA将有两种状态。因此，声明3也是错误的。 所以正确的选择是（D）。

本文由Sonal Tuteja撰稿。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。