有限自动机简介

有限自动机（FA）是识别模式的最简单机器。有限自动机或有限状态机是一种具有五个元素或元组的抽象机器。它有一组从一个状态移动到另一个状态的状态和规则，但它取决于应用的输入符号。基本上，它是数字计算机的抽象模型。下图显示了一些基本的自动化功能。

图： 有限自动机的特征

上图显示了自动机的以下功能：

1. 输入
2. 输出
3. 自动机状态
4. 国家关系
5. 输出关系

有限自动机由以下部分组成：

Q : Finite set of states.Σ : set of Input Symbols.q : Initial state.F : set of Final States.δ : Transition Function.

机器的正式规格是

{ Q, Σ, q, F, δ }

FA分为两种类型：

1） 确定性有限自动机（DFA） –

DFA consists of 5 tuples {Q, Σ, q, F, δ}. Q : set of all states.Σ : set of input symbols. ( Symbols which machine takes as input )q : Initial state. ( Starting state of a machine )F : set of final state.δ : Transition Function, defined as δ : Q X Σ --> Q.

在DFA中，对于特定的输入字符，机器只进入一种状态。每个输入符号的每个状态都定义了一个转换函数。此外，在DFA中，不允许空（或ε）移动，即DFA不能在没有任何输入字符的情况下更改状态。

例如，在DFA下方，∑={0，1}接受以0结尾的所有字符串。

图： 带∑={0，1}的DFA

需要注意的一点是， 对于一个模式，可以有许多可能的DFA .通常首选州数最少的DFA。

2） 非确定性有限自动机（NFA） NFA与DFA类似，除了以下附加功能：

1. 允许零（或ε）移动，即它可以在不读取符号的情况下向前移动。
2. 能够为特定输入传输到任意数量的状态。

然而，以上这些功能并没有为NFA增加任何功能。如果我们在力量方面比较两者，两者都是等价的。

由于上述附加功能，NFA具有不同的转换功能，其余功能与DFA相同。

δ: Transition Functionδ:  Q X (Σ U ε ) --> 2 ^ Q. 

正如你在过渡函数中所看到的，对于任何输入，包括null（或ε），NFA都可以进入任何状态。 例如，下面是针对上述问题的NFA。

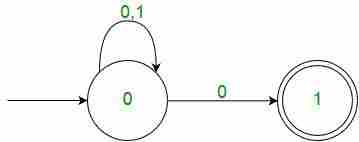
NFA

需要注意的一点是， 在NFA中，如果输入字符串的任何路径指向最终状态，则输入字符串 是 认可的 例如，在上述NFA中，输入字符串“00”有多个路径。由于其中一条路径通向最终状态，上述NFA接受“00”。

一些要点：

• 正当理由：

In case of DFAδ : Q X Σ --> QIn case of NFAδ : Q X Σ --> 2Q

1. NFA和DFA具有相同的功率，每个NFA都可以转换为DFA。
2. DFA和NFA中都可以有多个最终状态。
3. NFA更多的是一个理论概念。
4. DFA用于编译器中的词法分析。

参见关于 正则表达式与有限自动机 .

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论