数学|集合运算（集合论）

协会

集合A和B的并集，用A表示∪ B、 是属于集合A或集合B或两者的一组不同元素。

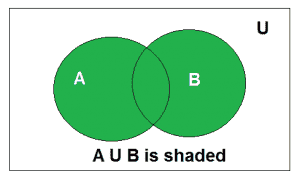
A的维恩图∪ B

上面是U B的维恩图。

Example: Find the union of A = {2, 3, 4} and B = {3, 4, 5}; Solution : A ∪ B = {2, 3, 4, 5}.

十字路口

集合A和B的交集，用A表示∩ B、 是同时属于A和B的元素集，即A和B中的公共元素集。

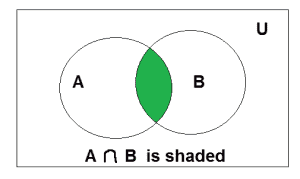
A的维恩图∩ B

上面是一个模型的维恩图∩ B。

Example: Find the intersection of A = {2, 3, 4} and B = {3, 4, 5} Solution : A ∩ B = {3, 4}.

不相交

如果两个集合的交集为空集，则称其为不相交。i、 集合没有公共元素。

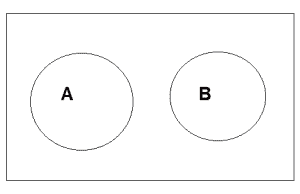
上面是不相交B的维恩图。

Example: Let A = {1, 3, 5, 7, 9} and B = { 2, 4, 6, 8}  A and B are disjoint sets since both of them have no common elements.

设定差异

集合之间的差异用“A–B”表示，这是一个集合，包含A中的元素，但不包含B中的元素。也就是说，除了B中的元素之外，A中的所有元素。

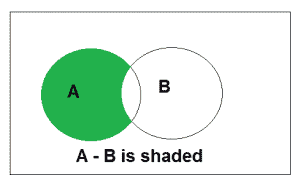
以上是A-B的维恩图。

Example: If A = {1, 2, 3, 4, 5} and B = { 2, 4, 6, 8}, find A-BSolution: A-B = {1, 3, 5}

补足

集合a的补码，用a表示 ^C 是除A中的元素外的所有元素的集合。集合A的补集是U–A。

上面是一个模型的维恩图 ^C

Example: Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {2, 4, 6, 8}.Find ACSolution: AC = U-A = {1, 3, 5, 7, 9, 10}

加减法

增加A组和B组，称为 明可夫斯基加法 ，是一个集合，其中的元素是两个集合中每个可能的元素对的总和（即一个元素来自集合A，另一个来自集合B）。 集合减法遵循相同的规则，但对元素进行减法运算。需要注意的是，这些操作仅在数字数据类型上可操作。即使以其他方式操作，它也只是一个没有任何意义的象征性表示。此外，很容易看出集合加法是可交换的，而减法不是。

有关加法和减法，请参阅 这就是答案。

[Tex]A-B=Acap ar{B}[/Tex]

1. 关联属性： A.∪ （B）∪ C） =（A）∪ B）∪ C和A∩ （B）∩ C） =（A）∩ B）∩ C
2. 交换性质： A.∪ B=B∪ A和A∩ B=B∩ A.
3. 工会的身份和财产： A.∪ φ=A
4. 空集的交集属性： A.∩ φ = φ
5. 分配属性： A.∪ （B）∩ C） =（A）∪ B）∩ （A）∪ C） 交叉口也是如此。