多边形裁剪| Sutherland–Hodgman算法-yiteyi-C++库

给出了一个凸多边形和一个凸裁剪区域。任务是使用Sutherland–Hodgman算法剪裁多边形边。输入是以多边形顶点的形式输入的 顺时针顺序 .

null

例如：

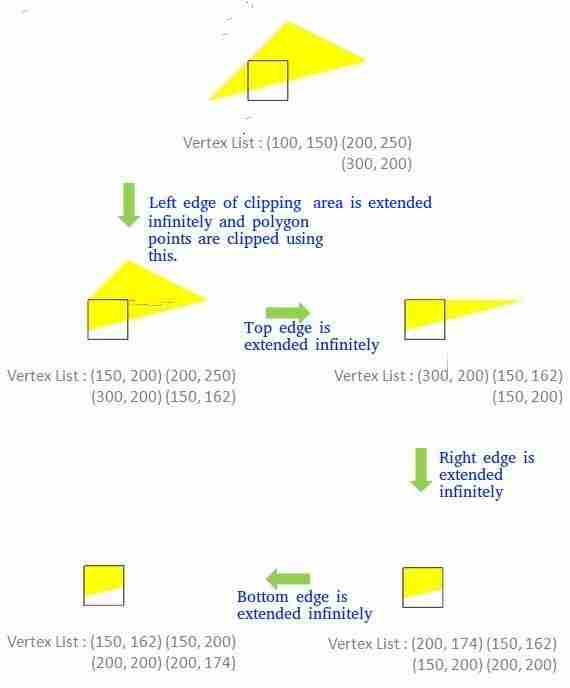
Input : Polygon : (100,150), (200,250), (300,200)
        Clipping Area : (150,150), (150,200), (200,200), 
                            (200,150) i.e. a Square    
Output : (150, 162) (150, 200) (200, 200) (200, 174) 


Example 2
Input : Polygon : (100,150), (200,250), (300,200)
        Clipping Area : (100,300), (300,300), (200,100) 
Output : (242, 185) (166, 166) (150, 200) (200, 250) (260, 220)

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

算法概述：

Consider each edge e of clipping Area  and do following:
   a) Clip given polygon against e.

如何根据剪裁区域的边缘进行剪裁？ 将（剪裁区域的）边无限延伸以创建边界，并使用该边界剪裁所有顶点。生成的新顶点列表将以顺时针方式传递到剪辑多边形的下一条边，直到所有边都已使用。

给定多边形的任意给定边与当前剪切边e之间存在四种可能的情况。

两个顶点都在内部： 只有第二个顶点被添加到输出列表中
第一个顶点在外部，第二个顶点在内部： 边与剪辑边界的交点和第二个顶点都将添加到输出列表中
第一个顶点在内侧，第二个顶点在外侧： 只有边与剪辑边界的交点才会添加到输出列表中
两个顶点都在外部： 没有顶点添加到输出列表中

在实现算法之前，需要讨论两个子问题：-

决定一个点是在裁剪器多边形的内部还是外部 如果裁剪器多边形的顶点是按顺时针顺序给定的，则所有位于该多边形上的点右侧其中一条修剪器边位于该多边形内。这可以使用以下公式计算：

查找边与剪辑边界的交点的步骤 如果每条直线（1,2和3,4）的两个点已知，则可以使用以下公式计算它们的交点：-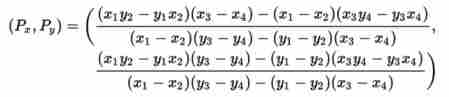

                     // C++ program for implementing Sutherland–Hodgman                   
                     // algorithm for polygon clipping                   
                     #include<iostream>                   
                     using                               namespace                               std;                   
                             
                     const                               int                               MAX_POINTS = 20;                   
                             
                     // Returns x-value of point of intersection of two                   
                     // lines                   
                     int                               x_intersect(                               int                               x1,                               int                               y1,                               int                               x2,                               int                               y2,                   
                                         int                               x3,                               int                               y3,                               int                               x4,                               int                               y4)                   
                     {                   
                                         int                               num = (x1*y2 - y1*x2) * (x3-x4) -                   
                                         (x1-x2) * (x3*y4 - y3*x4);                   
                                         int                               den = (x1-x2) * (y3-y4) - (y1-y2) * (x3-x4);                   
                                         return                               num/den;                   
                     }                   
                             
                     // Returns y-value of point of intersection of                   
                     // two lines                   
                     int                               y_intersect(                               int                               x1,                               int                               y1,                               int                               x2,                               int                               y2,                   
                                         int                               x3,                               int                               y3,                               int                               x4,                               int                               y4)                   
                     {                   
                                         int                               num = (x1*y2 - y1*x2) * (y3-y4) -                   
                                         (y1-y2) * (x3*y4 - y3*x4);                   
                                         int                               den = (x1-x2) * (y3-y4) - (y1-y2) * (x3-x4);                   
                                         return                               num/den;                   
                     }                   
                             
                     // This functions clips all the edges w.r.t one clip                   
                     // edge of clipping area                   
                     void                               clip(                               int                               poly_points[][2],                               int                               &poly_size,                   
                                         int                               x1,                               int                               y1,                               int                               x2,                               int                               y2)                   
                     {                   
                                         int                               new_points[MAX_POINTS][2], new_poly_size = 0;                   
                             
                                         // (ix,iy),(kx,ky) are the co-ordinate values of                   
                                         // the points                   
                                         for                               (                               int                               i = 0; i < poly_size; i++)                   
                                         {                   
                                         // i and k form a line in polygon                   
                                         int                               k = (i+1) % poly_size;                   
                                         int                               ix = poly_points[i][0], iy = poly_points[i][1];                   
                                         int                               kx = poly_points[k][0], ky = poly_points[k][1];                   
                             
                                         // Calculating position of first point                   
                                         // w.r.t. clipper line                   
                                         int                               i_pos = (x2-x1) * (iy-y1) - (y2-y1) * (ix-x1);                   
                             
                                         // Calculating position of second point                   
                                         // w.r.t. clipper line                   
                                         int                               k_pos = (x2-x1) * (ky-y1) - (y2-y1) * (kx-x1);                   
                             
                                         // Case 1 : When both points are inside                   
                                         if                               (i_pos < 0  && k_pos < 0)                   
                                         {                   
                                         //Only second point is added                   
                                         new_points[new_poly_size][0] = kx;                   
                                         new_points[new_poly_size][1] = ky;                   
                                         new_poly_size++;                   
                                         }                   
                             
                                         // Case 2: When only first point is outside                   
                                         else                               if                               (i_pos >= 0  && k_pos < 0)                   
                                         {                   
                                         // Point of intersection with edge                   
                                         // and the second point is added                   
                                         new_points[new_poly_size][0] = x_intersect(x1,                   
                                         y1, x2, y2, ix, iy, kx, ky);                   
                                         new_points[new_poly_size][1] = y_intersect(x1,                   
                                         y1, x2, y2, ix, iy, kx, ky);                   
                                         new_poly_size++;                   
                             
                                         new_points[new_poly_size][0] = kx;                   
                                         new_points[new_poly_size][1] = ky;                   
                                         new_poly_size++;                   
                                         }                   
                             
                                         // Case 3: When only second point is outside                   
                                         else                               if                               (i_pos < 0  && k_pos >= 0)                   
                                         {                   
                                         //Only point of intersection with edge is added                   
                                         new_points[new_poly_size][0] = x_intersect(x1,                   
                                         y1, x2, y2, ix, iy, kx, ky);                   
                                         new_points[new_poly_size][1] = y_intersect(x1,                   
                                         y1, x2, y2, ix, iy, kx, ky);                   
                                         new_poly_size++;                   
                                         }                   
                             
                                         // Case 4: When both points are outside                   
                                         else                   
                                         {                   
                                         //No points are added                   
                                         }                   
                                         }                   
                             
                                         // Copying new points into original array                   
                                         // and changing the no. of vertices                   
                                         poly_size = new_poly_size;                   
                                         for                               (                               int                               i = 0; i < poly_size; i++)                   
                                         {                   
                                         poly_points[i][0] = new_points[i][0];                   
                                         poly_points[i][1] = new_points[i][1];                   
                                         }                   
                     }                   
                             
                     // Implements Sutherland–Hodgman algorithm                   
                     void                               suthHodgClip(                               int                               poly_points[][2],                               int                               poly_size,                   
                                         int                               clipper_points[][2],                               int                               clipper_size)                   
                     {                   
                                         //i and k are two consecutive indexes                   
                                         for                               (                               int                               i=0; i<clipper_size; i++)                   
                                         {                   
                                         int                               k = (i+1) % clipper_size;                   
                             
                                         // We pass the current array of vertices, it's size                   
                                         // and the end points of the selected clipper line                   
                                         clip(poly_points, poly_size, clipper_points[i][0],                   
                                         clipper_points[i][1], clipper_points[k][0],                   
                                         clipper_points[k][1]);                   
                                         }                   
                             
                                         // Printing vertices of clipped polygon                   
                                         for                               (                               int                               i=0; i < poly_size; i++)                   
                                         cout <<                               '('                               << poly_points[i][0] <<                   
                                         ", "                               << poly_points[i][1] <<                               ") "                               ;                   
                     }                   
                             
                     //Driver code                   
                     int                               main()                   
                     {                   
                                         // Defining polygon vertices in clockwise order                   
                                         int                               poly_size = 3;                   
                                         int                               poly_points[20][2] = {{100,150}, {200,250},                   
                                         {300,200}};                   
                             
                                         // Defining clipper polygon vertices in clockwise order                   
                                         // 1st Example with square clipper                   
                                         int                               clipper_size = 4;                   
                                         int                               clipper_points[][2] = {{150,150}, {150,200},                   
                                         {200,200}, {200,150} };                   
                             
                                         // 2nd Example with triangle clipper                   
                                         /*int clipper_size = 3;                   
                                         int clipper_points[][2] = {{100,300}, {300,300},                   
                                         {200,100}};*/                   
                             
                                         //Calling the clipping function                   
                                         suthHodgClip(poly_points, poly_size, clipper_points,                   
                                         clipper_size);                   
                             
                                         return                               0;                   
                     }                   

输出：

(150, 162) (150, 200) (200, 200) (200, 174)

相关文章： 线裁剪|集1（科恩-萨瑟兰算法）计算机图形学中的点裁剪算法

本文由 纳巴内特·罗伊 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章