本文讨论了排序数组中的插入和删除操作。
null
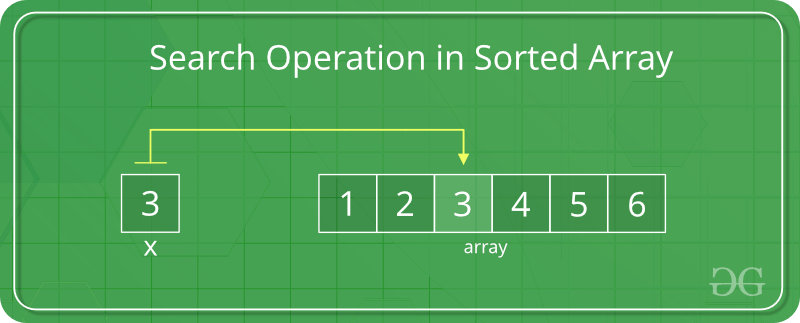
搜索操作 在排序数组中,可以使用 二进制搜索 .
C++
// C++ program to implement binary search in sorted array #include <bits/stdc++.h> using namespace std; int binarySearch( int arr[], int low, int high, int key) { if (high < low) return -1; int mid = (low + high) / 2; /*low + (high - low)/2;*/ if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key); return binarySearch(arr, low, (mid - 1), key); } /* Driver code */ int main() { // Let us search 3 in below array int arr[] = { 5, 6, 7, 8, 9, 10 }; int n, key; n = sizeof (arr) / sizeof (arr[0]); key = 10; cout << "Index: " << binarySearch(arr, 0, n - 1, key) << endl; return 0; } // This code is contributed by NamrataSrivastava1 |
C
// C program to implement binary search in sorted array #include <stdio.h> int binarySearch( int arr[], int low, int high, int key) { if (high < low) return -1; int mid = (low + high) / 2; /*low + (high - low)/2;*/ if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key); return binarySearch(arr, low, (mid - 1), key); } /* Driver Code */ int main() { // Let us search 3 in below array int arr[] = { 5, 6, 7, 8, 9, 10 }; int n, key; n = sizeof (arr) / sizeof (arr[0]); key = 10; printf ( "Index: %d" , binarySearch(arr, 0, n-1, key)); return 0; } |
JAVA
// Java program to implement binary // search in a sorted array class Main { // function to implement // binary search static int binarySearch( int arr[], int low, int high, int key) { if (high < low) return - 1 ; /*low + (high - low)/2;*/ int mid = (low + high) / 2 ; if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1 ), high, key); return binarySearch(arr, low, (mid - 1 ), key); } /* Driver Code*/ public static void main(String[] args) { int arr[] = { 5 , 6 , 7 , 8 , 9 , 10 }; int n, key; n = arr.length - 1 ; key = 10 ; System.out.println( "Index: " + binarySearch(arr, 0 , n, key)); } } |
Python3
# python 3 program to implement # binary search in sorted array def binarySearch(arr, low, high, key): # low + (high - low)/2 mid = (low + high) / 2 if (key = = arr[ int (mid)]): return mid if (key > arr[ int (mid)]): return binarySearch(arr, (mid + 1 ), high, key) if (key < arr[ int (mid)]): return binarySearch(arr,low, (mid - 1 ), key) return 0 # Driver program to check above functions # Let us search 3 in below array arr = [ 5 , 6 , 7 , 8 , 9 , 10 ] n = len (arr) key = 10 print ( "Index:" , int (binarySearch(arr, 0 , n - 1 , key) )) # This code is contributed by # Smitha Dinesh Semwal |
C#
// C# program to implement binary // search in a sorted array using System; public class GFG { // function to implement // binary search public static int binarySearch( int [] arr, int low, int high, int key) { if (high < low) { return -1; } /*low + (high - low)/2;*/ int mid = (low + high) / 2; if (key == arr[mid]) { return mid; } if (key > arr[mid]) { return binarySearch(arr, (mid + 1), high, key); } return binarySearch(arr, low, (mid - 1), key); } /* Driver Code */ public static void Main( string [] args) { int [] arr = new int [] { 5, 6, 7, 8, 9, 10 }; int n, key; n = arr.Length; key = 10; Console.WriteLine( "Index: " + binarySearch(arr, 0, n-1, key)); } } // This code is contributed by Shrikant13 |
PHP
// PHP program to implement // binary search in sorted array <?php function binarySearch( $arr , $low , $high , $key ) { if ( $high < $low ) return -1; // low + (high - low)/2 $mid = ( $low + $high ) / 2; if ( $key == $arr [(int) $mid ]) return $mid ; if ( $key > $arr [(int) $mid ]) return binarySearch( $arr , ( $mid + 1), $high , $key ); return (binarySearch( $arr , $low , ( $mid -1), $key )); } // Driver Code // Let us search 3 in below array $arr = array (5, 6, 7, 8, 9, 10); $n = count ( $arr ); $key = 10; echo "Index: " , (int)binarySearch( $arr , 0, $n -1, $key ); // This code is contributed by // Srathore ?> |
Javascript
<script> // Javascript program to implement // binary search in sorted array function binarySearch( arr, low, high, key) { if (high < low) return -1; /*low + (high - low)/2;*/ let mid = Math.trunc((low + high) / 2); if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key); return binarySearch(arr, low, (mid - 1), key); } // Driver program // Let us search 3 in below array let arr = [ 5, 6, 7, 8, 9, 10 ]; let n, key; n = arr.length; key = 10; document.write( "Index: " + binarySearch(arr, 0, n - 1, key) + "</br>" ); </script> |
输出
Index: 5
搜索操作的时间复杂性: O(logn)[使用二进制搜索]
插入操作
在排序数组中,通过使用 二进制搜索 然后执行插入操作,然后移动元件。在未排序的数组中,插入操作比排序数组更快,因为我们不必关心元素放置的位置。

C++
// C++ program to implement insert operation in // an sorted array. #include <iostream> using namespace std; // Inserts a key in arr[] of given capacity. n is current // size of arr[]. This function returns n+1 if insertion // is successful, else n. int insertSorted( int arr[], int n, int key, int capacity) { // Cannot insert more elements if n is already // more than or equal to capacity if (n >= capacity) return n; int i; for (i = n - 1; (i >= 0 && arr[i] > key); i--) arr[i + 1] = arr[i]; arr[i + 1] = key; return (n + 1); } /* Driver code */ int main() { int arr[20] = { 12, 16, 20, 40, 50, 70 }; int capacity = sizeof (arr) / sizeof (arr[0]); int n = 6; int i, key = 26; cout<< "Before Insertion: " ; for (i = 0; i < n; i++) cout << arr[i] << " " ; // Inserting key n = insertSorted(arr, n, key, capacity); cout << "After Insertion: " ; for (i = 0; i < n; i++) cout << arr[i]<< " " ; return 0; } // This code is contributed by SHUBHAMSINGH10 |
C
// C program to implement insert operation in // an sorted array. #include <stdio.h> // Inserts a key in arr[] of given capacity. n is current // size of arr[]. This function returns n+1 if insertion // is successful, else n. int insertSorted( int arr[], int n, int key, int capacity) { // Cannot insert more elements if n is already // more than or equal to capacity if (n >= capacity) return n; int i; for (i = n - 1; (i >= 0 && arr[i] > key); i--) arr[i + 1] = arr[i]; arr[i + 1] = key; return (n + 1); } /* Driver program to test above function */ int main() { int arr[20] = { 12, 16, 20, 40, 50, 70 }; int capacity = sizeof (arr) / sizeof (arr[0]); int n = 6; int i, key = 26; printf ( "Before Insertion: " ); for (i = 0; i < n; i++) printf ( "%d " , arr[i]); // Inserting key n = insertSorted(arr, n, key, capacity); printf ( "After Insertion: " ); for (i = 0; i < n; i++) printf ( "%d " , arr[i]); return 0; } |
JAVA
// Java program to insert an // element in a sorted array class Main { // Inserts a key in arr[] of given // capacity. n is current size of arr[]. // This function returns n+1 if insertion // is successful, else n. static int insertSorted( int arr[], int n, int key, int capacity) { // Cannot insert more elements if n is already // more than or equal to capacity if (n >= capacity) return n; int i; for (i = n - 1 ; (i >= 0 && arr[i] > key); i--) arr[i + 1 ] = arr[i]; arr[i + 1 ] = key; return (n + 1 ); } /* Driver program to test above function */ public static void main(String[] args) { int arr[] = new int [ 20 ]; arr[ 0 ] = 12 ; arr[ 1 ] = 16 ; arr[ 2 ] = 20 ; arr[ 3 ] = 40 ; arr[ 4 ] = 50 ; arr[ 5 ] = 70 ; int capacity = arr.length; int n = 6 ; int key = 26 ; System.out.print( "Before Insertion: " ); for ( int i = 0 ; i < n; i++) System.out.print(arr[i] + " " ); // Inserting key n = insertSorted(arr, n, key, capacity); System.out.print( "After Insertion: " ); for ( int i = 0 ; i < n; i++) System.out.print(arr[i] + " " ); } } |
Python3
# Python3 program to implement insert # operation in an sorted array. # Inserts a key in arr[] of given capacity. # n is current size of arr[]. This function # returns n+1 if insertion is successful, else n. def insertSorted(arr, n, key, capacity): # Cannot insert more elements if n is # already more than or equal to capacity if (n > = capacity): return n i = n - 1 while i > = 0 and arr[i] > key: arr[i + 1 ] = arr[i] i - = 1 arr[i + 1 ] = key return (n + 1 ) # Driver Code arr = [ 12 , 16 , 20 , 40 , 50 , 70 ] for i in range ( 20 ): arr.append( 0 ) capacity = len (arr) n = 6 key = 26 print ( "Before Insertion: " , end = " " ); for i in range (n): print (arr[i], end = " " ) # Inserting key n = insertSorted(arr, n, key, capacity) print ( "After Insertion: " , end = "") for i in range (n): print (arr[i], end = " " ) # This code is contributed by Mohit Kumar |
C#
using System; // C# program to insert an // element in a sorted array public class GFG { // Inserts a key in arr[] of given // capacity. n is current size of arr[]. // This function returns n+1 if insertion // is successful, else n. public static int insertSorted( int [] arr, int n, int key, int capacity) { // Cannot insert more elements if n is already // more than or equal to capacity if (n >= capacity) { return n; } int i; for (i = n - 1; (i >= 0 && arr[i] > key); i--) { arr[i + 1] = arr[i]; } arr[i + 1] = key; return (n + 1); } /* Driver program to test above function */ public static void Main( string [] args) { int [] arr = new int [20]; arr[0] = 12; arr[1] = 16; arr[2] = 20; arr[3] = 40; arr[4] = 50; arr[5] = 70; int capacity = arr.Length; int n = 6; int key = 26; Console.Write( "Before Insertion: " ); for ( int i = 0; i < n; i++) { Console.Write(arr[i] + " " ); } // Inserting key n = insertSorted(arr, n, key, capacity); Console.Write( "After Insertion: " ); for ( int i = 0; i < n; i++) { Console.Write(arr[i] + " " ); } } } // This code is contributed by Shrikant13 |
Javascript
<script> // JavaScript program to insert an // element in a sorted array // Inserts a key in arr[] of given // capacity. n is current size of arr[]. // This function returns n+1 if insertion // is successful, else n. function insertSorted( arr, n, key, capacity) { // Cannot insert more elements if n is already // more than or equal to capacity if (n >= capacity) return n; var i; for (i = n - 1; (i >= 0 && arr[i] > key); i--) arr[i + 1] = arr[i]; arr[i + 1] = key; return (n + 1); } /* Driver program to test above function */ var arr = new Array(20); arr[0] = 12; arr[1] = 16; arr[2] = 20; arr[3] = 40; arr[4] = 50; arr[5] = 70; var capacity = arr.length; var n = 6; var key = 26; document.write( "Before Insertion: " ); for ( var i = 0; i < n; i++) document.write(arr[i] + " " ); // Inserting key n = insertSorted(arr, n, key, capacity); document.write( "<br>" + "After Insertion: " ); for ( var i = 0; i < n; i++) document.write(arr[i] + " " ); // This code is contributed by shivanisinghss2110 </script> |
输出
Before Insertion: 12 16 20 40 50 70 After Insertion: 12 16 20 26 40 50 70
插入操作的时间复杂性: O(n)[在最坏的情况下,可能必须移动所有元件]
删除操作
在删除操作中,使用二进制搜索来搜索要删除的元素,然后执行删除操作,然后移动元素。

C++
// C++ program to implement delete operation in a // sorted array #include <iostream> using namespace std; // To search a key to be deleted int binarySearch( int arr[], int low, int high, int key); /* Function to delete an element */ int deleteElement( int arr[], int n, int key) { // Find position of element to be deleted int pos = binarySearch(arr, 0, n - 1, key); if (pos == -1) { cout << "Element not found" ; return n; } // Deleting element int i; for (i = pos; i < n - 1; i++) arr[i] = arr[i + 1]; return n - 1; } int binarySearch( int arr[], int low, int high, int key) { if (high < low) return -1; int mid = (low + high) / 2; if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key); return binarySearch(arr, low, (mid - 1), key); } // Driver code int main() { int i; int arr[] = { 10, 20, 30, 40, 50 }; int n = sizeof (arr) / sizeof (arr[0]); int key = 30; cout << "Array before deletion" ; for (i = 0; i < n; i++) cout << arr[i] << " " ; n = deleteElement(arr, n, key); cout << "Array after deletion" ; for (i = 0; i < n; i++) cout << arr[i] << " " ; } // This code is contributed by shubhamsingh10 |
C
// C program to implement delete operation in a // sorted array #include <stdio.h> // To search a key to be deleted int binarySearch( int arr[], int low, int high, int key); /* Function to delete an element */ int deleteElement( int arr[], int n, int key) { // Find position of element to be deleted int pos = binarySearch(arr, 0, n - 1, key); if (pos == -1) { printf ( "Element not found" ); return n; } // Deleting element int i; for (i = pos; i < n - 1; i++) arr[i] = arr[i + 1]; return n - 1; } int binarySearch( int arr[], int low, int high, int key) { if (high < low) return -1; int mid = (low + high) / 2; if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key); return binarySearch(arr, low, (mid - 1), key); } // Driver code int main() { int i; int arr[] = { 10, 20, 30, 40, 50 }; int n = sizeof (arr) / sizeof (arr[0]); int key = 30; printf ( "Array before deletion" ); for (i = 0; i < n; i++) printf ( "%d " , arr[i]); n = deleteElement(arr, n, key); printf ( "Array after deletion" ); for (i = 0; i < n; i++) printf ( "%d " , arr[i]); } |
JAVA
// Java program to delete an // element from a sorted array class Main { // binary search static int binarySearch( int arr[], int low, int high, int key) { if (high < low) return - 1 ; int mid = (low + high) / 2 ; if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1 ), high, key); return binarySearch(arr, low, (mid - 1 ), key); } /* Function to delete an element */ static int deleteElement( int arr[], int n, int key) { // Find position of element to be deleted int pos = binarySearch(arr, 0 , n - 1 , key); if (pos == - 1 ) { System.out.println( "Element not found" ); return n; } // Deleting element int i; for (i = pos; i < n - 1 ; i++) arr[i] = arr[i + 1 ]; return n - 1 ; } /* Driver Code */ public static void main(String[] args) { int i; int arr[] = { 10 , 20 , 30 , 40 , 50 }; int n = arr.length; int key = 30 ; System.out.print( "Array before deletion:" ); for (i = 0 ; i < n; i++) System.out.print(arr[i] + " " ); n = deleteElement(arr, n, key); System.out.print( "Array after deletion:" ); for (i = 0 ; i < n; i++) System.out.print(arr[i] + " " ); } } |
Python3
# Python program to implement delete operation in a # sorted array #/* Function to delete an element */ def deleteElement(arr, n, key): # Find position of element to be deleted pos = binarySearch(arr, 0 , n - 1 , key) if (pos = = - 1 ): print ( "Element not found" ) return n # Deleting element for i in range (pos,n - 1 ): arr[i] = arr[i + 1 ] return n - 1 # To search a key to be deleted def binarySearch(arr, low, high, key): if (high < low): return - 1 mid = (low + high) / / 2 if (key = = arr[mid]): return mid if (key > arr[mid]): return binarySearch(arr, (mid + 1 ), high, key) return binarySearch(arr, low, (mid - 1 ), key) # Driver code arr = [ 10 , 20 , 30 , 40 , 50 ] n = len (arr) key = 30 print ( "Array before deletion" ) for i in range (n): print (arr[i],end = " " ) n = deleteElement(arr, n, key) print ( "Array after deletion" ) for i in range (n): print (arr[i],end = " " ) # This code is contributed by shubhamsingh10 |
C#
// C# program to delete an // element from a sorted array using System; public class GFG { // binary search static int binarySearch( int [] arr, int low, int high, int key) { if (high < low) return -1; int mid = (low + high) / 2; if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key); return binarySearch(arr, low, (mid - 1), key); } /* Function to delete an element */ static int deleteElement( int [] arr, int n, int key) { // Find position of element to be deleted int pos = binarySearch(arr, 0, n - 1, key); if (pos == -1) { Console.WriteLine( "Element not found" ); return n; } // Deleting element int i; for (i = pos; i < n - 1; i++) arr[i] = arr[i + 1]; return n - 1; } /* Driver Code */ public static void Main() { int i; int [] arr = { 10, 20, 30, 40, 50 }; int n = arr.Length; int key = 30; Console.Write( "Array before deletion:" ); for (i = 0; i < n; i++) Console.Write(arr[i] + " " ); n = deleteElement(arr, n, key); Console.Write( "Array after deletion:" ); for (i = 0; i < n; i++) Console.Write(arr[i] + " " ); } } // This code is contributed by Rajput-Ji |
Javascript
<script> // JavaScript program to delete an // element from a sorted array // binary search function binarySearch(arr, low, high, key) { if (high < low) return -1; let mid = (low + high) / 2; if (key == arr[mid]) return mid; if (key > arr[mid]) return binarySearch(arr, (mid + 1), high, key); return binarySearch(arr, low, (mid - 1), key); } /* Function to delete an element */ function deleteElement( arr, n, key) { // Find position of element to be deleted let pos = binarySearch(arr, 0, n - 1, key); if (pos == -1) { document.write( "Element not found" ); return n; } // Deleting element let i; for (i = pos; i < n - 1; i++) arr[i] = arr[i + 1]; return n - 1; } /* Driver Code */ let i; let arr = [ 10, 20, 30, 40, 50 ]; let n = arr.length; let key = 30; document.write( "Array before deletion:" ); for (i = 0; i < n; i++) document.write(arr[i] + " " ); n = deleteElement(arr, n, key); document.write( "<br>" + "Array after deletion:" ); for (i = 0; i < n; i++) document.write(arr[i] + " " ); // this code is contributed by shivanisinghss2110 </script> |
输出
Array before deletion 10 20 30 40 50 Array after deletion 10 20 40 50
删除操作的时间复杂度: O(n)[在最坏的情况下,可能必须移动所有元件]
?list=PLqM7alHXFySEQDk2MDfbwEdjd2svVJH9p
如果你喜欢GeekSforgeks,并且想贡献自己的力量,你也可以写一篇文章,然后把你的文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



