求解骑士巡游问题的Warnsdorff算法-yiteyi-C++库

问题： 骑士被放置在一块空棋盘的第一块，按照国际象棋规则移动，必须精确地访问每个方块一次。

null

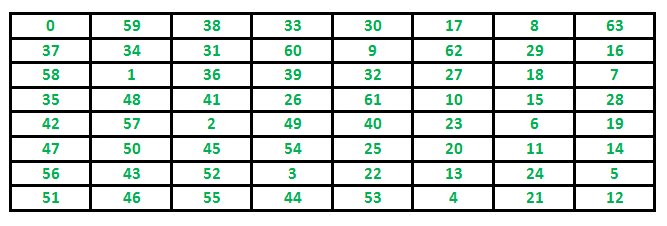
下面是Knight覆盖所有单元格的路径示例。下面的网格表示一个包含8 x 8个单元格的棋盘。单元格中的数字表示骑士的移动次数。

knight-tour-problem

我们讨论过求解骑士之旅的回溯算法 .在这个帖子里沃恩斯多夫启发法本文对此进行了讨论。 沃恩斯多夫规则：

我们可以从骑士在棋盘上的任何初始位置开始。
我们总是以最小的度数（最小的未访问的相邻数）移动到一个相邻的、未访问的正方形。

这种算法也可以更普遍地应用于任何图形。

一些定义：

如果P可以通过一个骑士的移动移动到Q，并且Q还没有被访问，那么位置Q可以从位置P访问。
位置P的可访问性是可从P访问的位置数。

算法：

将P设置为板上的随机初始位置
在P处用移动编号“1”标记电路板
从2移动到棋盘上的方块数时，请执行以下操作：
- 让我们成为从P。
- 将P设置为S中具有最小可达性的位置
- 用当前移动编号在P处标记棋盘
返回已标记的板-每个方块都将标记其访问的移动编号。

下面是上述算法的实现。

C++

                         // C++ program to for Kinight's tour problem using                       
                         // Warnsdorff's algorithm                       
                         #include <bits/stdc++.h>                       
                         #define N 8                       
           
                         // Move pattern on basis of the change of                       
                         // x coordinates and y coordinates respectively                       
                         static                                     int                                     cx[N] = {1,1,2,2,-1,-1,-2,-2};                       
                         static                                     int                                     cy[N] = {2,-2,1,-1,2,-2,1,-1};                       
           
                         // function restricts the knight to remain within                       
                         // the 8x8 chessboard                       
                         bool                                     limits(                                     int                                     x,                                     int                                     y)                       
                         {                       
                                                 return                                     ((x >= 0 && y >= 0) && (x < N && y < N));                       
                         }                       
           
                         /* Checks whether a square is valid and empty or not */                       
                         bool                                     isempty(                                     int                                     a[],                                     int                                     x,                                     int                                     y)                       
                         {                       
                                                 return                                     (limits(x, y)) && (a[y*N+x] < 0);                       
                         }                       
           
                         /* Returns the number of empty squares adjacent                       
                                                 to (x, y) */                       
                         int                                     getDegree(                                     int                                     a[],                                     int                                     x,                                     int                                     y)                       
                         {                       
                                                 int                                     count = 0;                       
                                                 for                                     (                                     int                                     i = 0; i < N; ++i)                       
                                                 if                                     (isempty(a, (x + cx[i]), (y + cy[i])))                       
                                                 count++;                       
           
                                                 return                                     count;                       
                         }                       
           
                         // Picks next point using Warnsdorff's heuristic.                       
                         // Returns false if it is not possible to pick                       
                         // next point.                       
                         bool                                     nextMove(                                     int                                     a[],                                     int                                     *x,                                     int                                     *y)                       
                         {                       
                                                 int                                     min_deg_idx = -1, c, min_deg = (N+1), nx, ny;                       
           
                                                 // Try all N adjacent of (*x, *y) starting                       
                                                 // from a random adjacent. Find the adjacent                       
                                                 // with minimum degree.                       
                                                 int                                     start =                                     rand                                     ()%N;                       
                                                 for                                     (                                     int                                     count = 0; count < N; ++count)                       
                                                 {                       
                                                 int                                     i = (start + count)%N;                       
                                                 nx = *x + cx[i];                       
                                                 ny = *y + cy[i];                       
                                                 if                                     ((isempty(a, nx, ny)) &&                       
                                                 (c = getDegree(a, nx, ny)) < min_deg)                       
                                                 {                       
                                                 min_deg_idx = i;                       
                                                 min_deg = c;                       
                                                 }                       
                                                 }                       
           
                                                 // IF we could not find a next cell                       
                                                 if                                     (min_deg_idx == -1)                       
                                                 return                                     false                                     ;                       
           
                                                 // Store coordinates of next point                       
                                                 nx = *x + cx[min_deg_idx];                       
                                                 ny = *y + cy[min_deg_idx];                       
           
                                                 // Mark next move                       
                                                 a[ny*N + nx] = a[(*y)*N + (*x)]+1;                       
           
                                                 // Update next point                       
                                                 *x = nx;                       
                                                 *y = ny;                       
           
                                                 return                                     true                                     ;                       
                         }                       
           
                         /* displays the chessboard with all the                       
                                                 legal knight's moves */                       
                         void                                     print(                                     int                                     a[])                       
                         {                       
                                                 for                                     (                                     int                                     i = 0; i < N; ++i)                       
                                                 {                       
                                                 for                                     (                                     int                                     j = 0; j < N; ++j)                       
                                                 printf                                     (                                     "%d	"                                     ,a[j*N+i]);                       
                                                 printf                                     (                                     ""                                     );                       
                                                 }                       
                         }                       
           
                         /* checks its neighbouring squares */                       
                         /* If the knight ends on a square that is one                       
                                                 knight's move from the beginning square,                       
                                                 then tour is closed */                       
                         bool                                     neighbour(                                     int                                     x,                                     int                                     y,                                     int                                     xx,                                     int                                     yy)                       
                         {                       
                                                 for                                     (                                     int                                     i = 0; i < N; ++i)                       
                                                 if                                     (((x+cx[i]) == xx)&&((y + cy[i]) == yy))                       
                                                 return                                     true                                     ;                       
           
                                                 return                                     false                                     ;                       
                         }                       
           
                         /* Generates the legal moves using warnsdorff's                       
                                                 heuristics. Returns false if not possible */                       
                         bool                                     findClosedTour()                       
                         {                       
                                                 // Filling up the chessboard matrix with -1's                       
                                                 int                                     a[N*N];                       
                                                 for                                     (                                     int                                     i = 0; i< N*N; ++i)                       
                                                 a[i] = -1;                       
           
                                                 // Random initial position                       
                                                 int                                     sx =                                     rand                                     ()%N;                       
                                                 int                                     sy =                                     rand                                     ()%N;                       
           
                                                 // Current points are same as initial points                       
                                                 int                                     x = sx, y = sy;                       
                                                 a[y*N+x] = 1;                                     // Mark first move.                       
           
                                                 // Keep picking next points using                       
                                                 // Warnsdorff's heuristic                       
                                                 for                                     (                                     int                                     i = 0; i < N*N-1; ++i)                       
                                                 if                                     (nextMove(a, &x, &y) == 0)                       
                                                 return                                     false                                     ;                       
           
                                                 // Check if tour is closed (Can end                       
                                                 // at starting point)                       
                                                 if                                     (!neighbour(x, y, sx, sy))                       
                                                 return                                     false                                     ;                       
           
                                                 print(a);                       
                                                 return                                     true                                     ;                       
                         }                       
           
                         // Driver code                       
                         int                                     main()                       
                         {                       
                                                 // To make sure that different random                       
                                                 // initial positions are picked.                       
                                                 srand                                     (                                     time                                     (NULL));                       
           
                                                 // While we don't get a solution                       
                                                 while                                     (!findClosedTour())                       
                                                 {                       
                                                 ;                       
                                                 }                       
           
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to for Kinight's tour problem using                       
                         // Warnsdorff's algorithm                       
                         import                                     java.util.concurrent.ThreadLocalRandom;                       
           
                         class                                     GFG                       
                         {                       
                                                 public                                     static                                     final                                     int                                     N =                                     8                                     ;                       
           
                                                 // Move pattern on basis of the change of                       
                                                 // x coordinates and y coordinates respectively                       
                                                 public                                     static                                     final                                     int                                     cx[] = {                                     1                                     ,                                     1                                     ,                                     2                                     ,                                     2                                     , -                                     1                                     , -                                     1                                     , -                                     2                                     , -                                     2                                     };                       
                                                 public                                     static                                     final                                     int                                     cy[] = {                                     2                                     , -                                     2                                     ,                                     1                                     , -                                     1                                     ,                                     2                                     , -                                     2                                     ,                                     1                                     , -                                     1                                     };                       
           
                                                 // function restricts the knight to remain within                       
                                                 // the 8x8 chessboard                       
                                                 boolean                                     limits(                                     int                                     x,                                     int                                     y)                       
                                                 {                       
                                                 return                                     ((x >=                                     0                                     && y >=                                     0                                     ) &&                       
                                                 (x < N && y < N));                       
                                                 }                       
           
                                                 /* Checks whether a square is valid and                       
                                                 empty or not */                       
                                                 boolean                                     isempty(                                     int                                     a[],                                     int                                     x,                                     int                                     y)                       
                                                 {                       
                                                 return                                     (limits(x, y)) && (a[y * N + x] <                                     0                                     );                       
                                                 }                       
           
                                                 /* Returns the number of empty squares                       
                                                 adjacent to (x, y) */                       
                                                 int                                     getDegree(                                     int                                     a[],                                     int                                     x,                                     int                                     y)                       
                                                 {                       
                                                 int                                     count =                                     0                                     ;                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < N; ++i)                       
                                                 if                                     (isempty(a, (x + cx[i]),                       
                                                 (y + cy[i])))                       
                                                 count++;                       
           
                                                 return                                     count;                       
                                                 }                       
           
                                                 // Picks next point using Warnsdorff's heuristic.                       
                                                 // Returns false if it is not possible to pick                       
                                                 // next point.                       
                                                 Cell nextMove(                                     int                                     a[], Cell cell)                       
                                                 {                       
                                                 int                                     min_deg_idx = -                                     1                                     , c,                       
                                                 min_deg = (N +                                     1                                     ), nx, ny;                       
           
                                                 // Try all N adjacent of (*x, *y) starting                       
                                                 // from a random adjacent. Find the adjacent                       
                                                 // with minimum degree.                       
                                                 int                                     start = ThreadLocalRandom.current().nextInt(                                     1000                                     ) % N;                       
                                                 for                                     (                                     int                                     count =                                     0                                     ; count < N; ++count)                       
                                                 {                       
                                                 int                                     i = (start + count) % N;                       
                                                 nx = cell.x + cx[i];                       
                                                 ny = cell.y + cy[i];                       
                                                 if                                     ((isempty(a, nx, ny)) &&                       
                                                 (c = getDegree(a, nx, ny)) < min_deg)                       
                                                 {                       
                                                 min_deg_idx = i;                       
                                                 min_deg = c;                       
                                                 }                       
                                                 }                       
           
                                                 // IF we could not find a next cell                       
                                                 if                                     (min_deg_idx == -                                     1                                     )                       
                                                 return                                     null                                     ;                       
           
                                                 // Store coordinates of next point                       
                                                 nx = cell.x + cx[min_deg_idx];                       
                                                 ny = cell.y + cy[min_deg_idx];                       
           
                                                 // Mark next move                       
                                                 a[ny * N + nx] = a[(cell.y) * N +                       
                                                 (cell.x)] +                                     1                                     ;                       
           
                                                 // Update next point                       
                                                 cell.x = nx;                       
                                                 cell.y = ny;                       
           
                                                 return                                     cell;                       
                                                 }                       
           
                                                 /* displays the chessboard with all the                       
                                                 legal knight's moves */                       
                                                 void                                     print(                                     int                                     a[])                       
                                                 {                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < N; ++i)                       
                                                 {                       
                                                 for                                     (                                     int                                     j =                                     0                                     ; j < N; ++j)                       
                                                 System.out.printf(                                     "%d	"                                     , a[j * N + i]);                       
                                                 System.out.printf(                                     ""                                     );                       
                                                 }                       
                                                 }                       
           
                                                 /* checks its neighbouring squares */                       
                                                 /* If the knight ends on a square that is one                       
                                                 knight's move from the beginning square,                       
                                                 then tour is closed */                       
                                                 boolean                                     neighbour(                                     int                                     x,                                     int                                     y,                                     int                                     xx,                                     int                                     yy)                       
                                                 {                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < N; ++i)                       
                                                 if                                     (((x + cx[i]) == xx) &&                       
                                                 ((y + cy[i]) == yy))                       
                                                 return                                     true                                     ;                       
           
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 /* Generates the legal moves using warnsdorff's                       
                                                 heuristics. Returns false if not possible */                       
                                                 boolean                                     findClosedTour()                       
                                                 {                       
                                                 // Filling up the chessboard matrix with -1's                       
                                                 int                                     a[] =                                     new                                     int                                     [N * N];                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < N * N; ++i)                       
                                                 a[i] = -                                     1                                     ;                       
           
                                                 // initial position                       
                                                 int                                     sx =                                     3                                     ;                       
                                                 int                                     sy =                                     2                                     ;                       
           
                                                 // Current points are same as initial points                       
                                                 Cell cell =                                     new                                     Cell(sx, sy);                       
           
                                                 a[cell.y * N + cell.x] =                                     1                                     ;                                     // Mark first move.                       
           
                                                 // Keep picking next points using                       
                                                 // Warnsdorff's heuristic                       
                                                 Cell ret =                                     null                                     ;                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < N * N -                                     1                                     ; ++i)                       
                                                 {                       
                                                 ret = nextMove(a, cell);                       
                                                 if                                     (ret ==                                     null                                     )                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // Check if tour is closed (Can end                       
                                                 // at starting point)                       
                                                 if                                     (!neighbour(ret.x, ret.y, sx, sy))                       
                                                 return                                     false                                     ;                       
           
                                                 print(a);                       
                                                 return                                     true                                     ;                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     main(String[] args)                       
                                                 {                       
                                                 // While we don't get a solution                       
                                                 while                                     (!                                     new                                     GFG().findClosedTour())                       
                                                 {                       
                                                 ;                       
                                                 }                       
                                                 }                       
                         }                       
           
                         class                                     Cell                       
                         {                       
                                                 int                                     x;                       
                                                 int                                     y;                       
           
                                                 public                                     Cell(                                     int                                     x,                                     int                                     y)                       
                                                 {                       
                                                 this                                     .x = x;                       
                                                 this                                     .y = y;                       
                                                 }                       
                         }                       
           
                         // This code is contributed by SaeedZarinfam                       

输出：

59    14    63    32    1    16    19    34    62    31    60    15    56    33    2    17    13    58    55    64    49    18    35    20    30    61    42    57    54    51    40    3    43    12    53    50    41    48    21    36    26    29    44    47    52    39    4    7    11    46    27    24    9    6    37    22    28    25    10    45    38    23    8    5

哈密顿路径问题通常是NP难问题。在实践中，沃恩斯多夫的启发式算法成功地在线性时间内找到了一个解决方案。

你知道吗？ “在一个8×8的电路板上，有26534728821064个定向闭合回路（即沿着同一条路径的两个反向回路，以及旋转和反射回路，分别计算）。无向闭合回路的数量是这个数字的一半，因为每个回路都可以反向追踪！”

本文由 乌达拉克·巴杜里 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章