我们遇到了各种各样的问题,比如字符串中最大长度的回文,回文子串的数量,以及更多关于回文子串的有趣问题。大多数回文子串问题都有一些dpo(n) 2. )解(n是给定字符串的长度)或者我们有一个复杂的算法,比如 马纳彻算法 在线性时间内解决回文问题。
在本文中,我们将研究一种有趣的数据结构,它将以更简单的方式解决上述所有类似问题。这种数据结构是由 米哈伊尔·鲁宾奇 .
Features of Palindromic Tree : Online query and updation
Easy to implement
Very Fast
回文树的结构
回文树的实际结构是 接近有向图 它实际上是两棵树的合并结构,它们共享一些公共节点(为了更好地理解,请参见下图)。树节点通过存储索引来存储给定字符串的回文子字符串。 此树由两种类型的边组成: 1) 插入边(加权边) 2) 最大回文后缀(未加权)
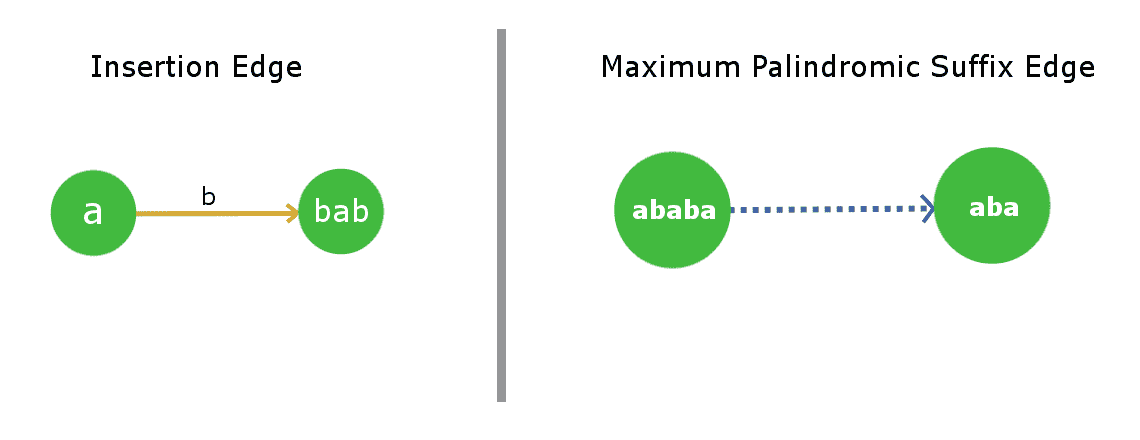
插入边缘: 从节点插入边 U 到 五、 有点分量 十、 意味着节点v是通过在u处字符串的前端和末端插入x形成的。由于u已经是回文,因此节点v处生成的字符串也将是回文。 十、 每个边缘都将是一个单独的字符。因此,一个节点最多可以有26条插入边(考虑较低的字母字符串)。我们将使用 橙色 在我们的绘画表现中的这一优势。
最大回文后缀边: 由于名称本身表明,对于节点,此边将指向其最大回文后缀字符串节点。我们不会将完整字符串本身视为最大回文后缀,因为这毫无意义(自循环)。为了简单起见,我们将其称为后缀边(后缀边是指除完整字符串外的最大后缀)。很明显,每个节点只有一个后缀边,因为我们不会在树中存储重复的字符串。我们将使用 蓝色虚线边缘 因为它的图像表现。
根节点及其约定: 此树/图数据结构将包含 2根虚拟节点 更确切地说,它被认为是两棵单独的树的根,它们被连接在一起。 根-1 将是一个虚拟节点,用于描述 长度=-1 (从实现的角度,你可以很容易地推断出我们为什么使用它)。 根-2 将是一个节点,它将描述 长度=0 .
根-1有一个与自身相连的后缀边(自循环),对于任何长度为-1的假想字符串,其最大回文后缀也将是假想的,因此这是合理的。现在,Root-2的后缀边也将连接到Root-1,因为对于空字符串(长度为0),没有长度小于0的真正回文后缀字符串。
构建回文树
要构建回文树,我们只需在字符串中逐个插入字符,直到到达其结尾,插入完成后,我们将使用回文树,它将包含给定字符串的所有不同回文子串。我们需要确保的是,每次插入一个新字符时,我们的回文树都能保持上述特征。让我们看看怎样才能做到这一点。
假设我们得到了一个字符串 s 有长度 L 我们在索引中插入了字符串 K (k
所以,要插入角色 s[k+1] ,我们只需要在树中找到字符串X,并将插入边从权重为s[k+1]的X定向到一个新节点,该节点包含 s[k+1]+X+s[k+1] .现在的主要工作是在有效时间内找到字符串X。正如我们所知,我们正在存储所有节点的后缀链接。因此,要用字符串X跟踪节点,我们只需要向下移动当前节点的后缀链接,即包含插入s[k]的节点。请参阅下图以更好地理解。
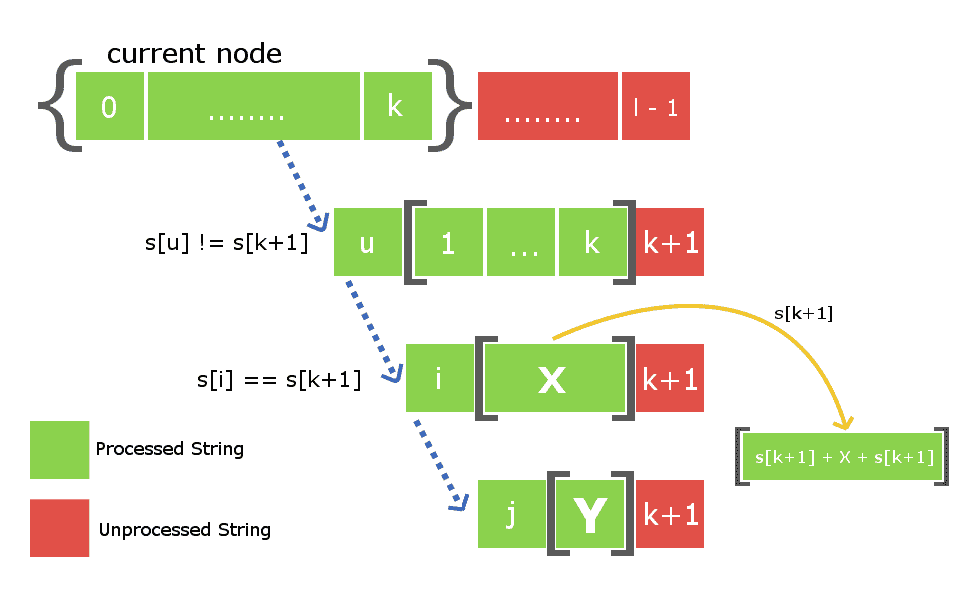
下图中的当前节点表明,在处理了从0到k的所有索引后,它是以索引k结尾的最大回文。蓝色虚线路径是当前节点到树中其他处理节点的后缀边的链接。字符串X将存在于位于后缀链接链上的其中一个节点中。我们所需要的就是通过在链上迭代找到它。
为了找到包含字符串X的所需节点,我们将把第k+1个字符放在后缀链接链中每个节点的末尾,并检查相应后缀链接字符串的第一个字符是否等于第k+1个字符。
一旦我们找到X字符串,我们将引导一个权重为s[k+1]的插入边,并将其链接到包含以索引k+1结尾的最大回文的新节点。下图中括号之间的数组元素是存储在树中的节点。
还有一件事要做。由于我们已经在这个s[k+1]插入处创建了一个新节点,因此我们还必须将其与其后缀链接子节点连接起来。再一次,为了这样做,我们将使用上面从节点X开始的后缀链接迭代来找到一些新字符串 Y 以至于 s[k+1]+Y+s[k+1] 是新创建节点的最大回文后缀。一旦找到它,我们将把新创建的节点的后缀链接与节点Y连接起来。
笔记 :当我们找到字符串X时,有两种可能性。第一种可能性是该字符串 s[k+1]Xs[k+1] 树中不存在,第二种可能性是它是否已经存在于树中。在第一种情况下,我们将以同样的方式进行,但在第二种情况下,我们不会单独创建一个新节点,而是将插入边从X链接到已经存在的节点 S[k+1]+X+S[k+1] 树中的节点。我们也不需要添加后缀链接,因为节点将已经包含其后缀链接。
考虑字符串s= 阿巴 “带着 长度=4 .
在初始状态下,我们将有两个伪根节点,一个长度为-1(一些虚构的字符串) 我 )第二个 无效的 长度为0的字符串。此时,我们还没有在树中插入任何字符。Root1,即长度为-1的根节点将是插入发生的当前节点。
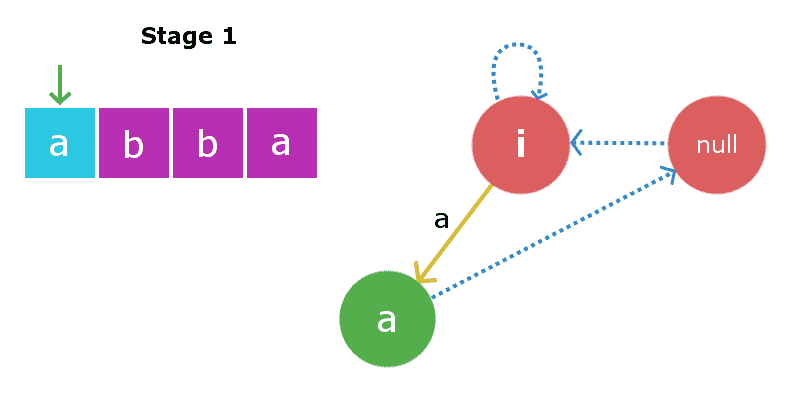
第一阶段:我们将插入 s[0] i、 e’ A. ‘.我们将从当前节点即Root1开始检查。在长度为-1的字符串的开头和结尾插入“a”将产生长度为1的字符串,该字符串将是“a”。因此,我们创建一个新节点“a”,并将插入边从root1直接插入到这个新节点。现在,长度为1的字符串的最大回文后缀字符串将是空字符串,因此其后缀链接将指向根2,即空字符串。现在,当前节点将是这个新节点“a”。
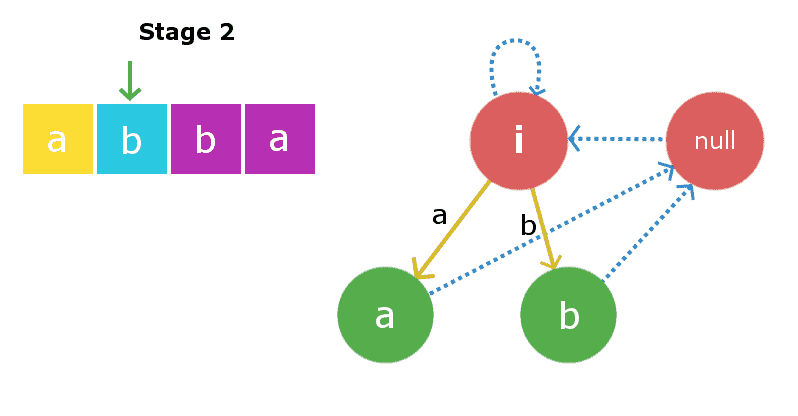
第二阶段:我们将插入 s[1] i、 e’ B ‘. 插入过程将从当前节点即“a”节点开始。我们将从当前节点开始遍历后缀链接链,直到找到合适的X字符串,所以在这里遍历后缀链接,我们再次发现root1是X字符串。再次在长度为-1的字符串中插入“b”将产生长度为1的字符串,即字符串“b”。此节点的后缀链接将转到空字符串,如上述插入所述。现在,当前节点将是这个新节点“b”。
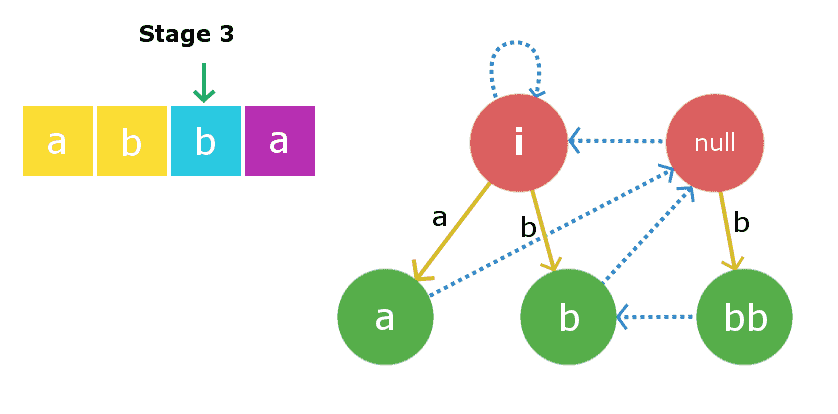
第三阶段:我们将插入 s[2] i、 e’ B ‘. 再次从当前节点开始,我们将遍历其后缀链接以找到所需的X字符串。在这种情况下,它被发现是root2,即空字符串,因为在空字符串的前面和结尾添加“b”会产生长度为2的回文“bb”。因此,我们将创建一个新节点“ bb “并将插入边从空字符串指向新创建的字符串。现在,当前节点的最大后缀回文将是节点“b”。因此,我们将把这个新创建的节点的后缀边链接到节点“b”。当前节点现在变成节点“bb”。
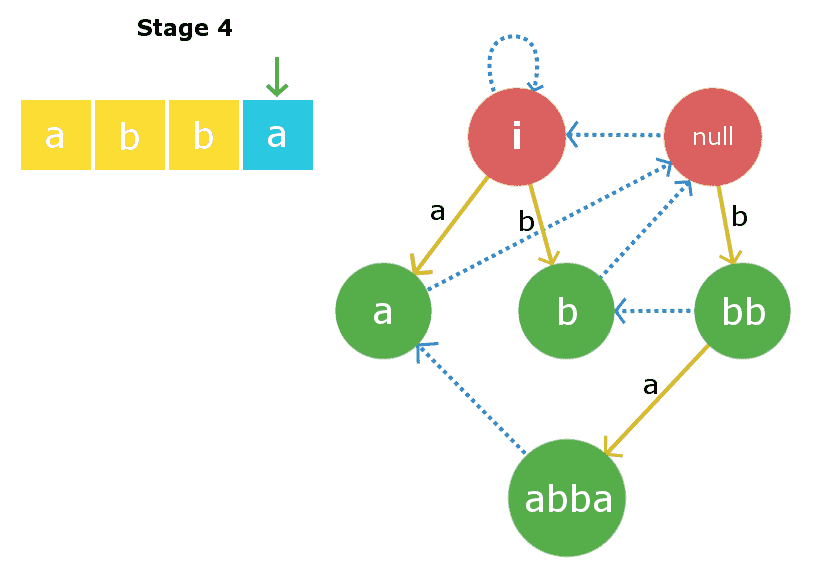
第四阶段:我们将插入 s[3] i、 e’ A. ‘. 插入过程从当前节点开始,在本例中,当前节点本身是最大的X字符串,因此 s[0]+X+s[3] 是回文。因此,我们将创建一个新节点“ 阿巴 并将插入边从当前节点“bb”链接到这个新创建的边权重为“a”的节点。现在,这个新创建的节点的链接的后缀将链接到节点“a”,因为它是最大的回文后缀。
上述实现的C++实现如下:
// C++ program to demonstrate working of // palindromic tree #include "bits/stdc++.h" using namespace std; #define MAXN 1000 struct Node { // store start and end indexes of current // Node inclusively int start, end; // stores length of substring int length; // stores insertion Node for all characters a-z int insertEdg[26]; // stores the Maximum Palindromic Suffix Node for // the current Node int suffixEdg; }; // two special dummy Nodes as explained above Node root1, root2; // stores Node information for constant time access Node tree[MAXN]; // Keeps track the current Node while insertion int currNode; string s; int ptr; void insert( int idx) { //STEP 1// /* search for Node X such that s[idx] X S[idx] is maximum palindrome ending at position idx iterate down the suffix link of currNode to find X */ int tmp = currNode; while ( true ) { int curLength = tree[tmp].length; if (idx - curLength >= 1 and s[idx] == s[idx-curLength-1]) break ; tmp = tree[tmp].suffixEdg; } /* Now we have found X .... * X = string at Node tmp * Check : if s[idx] X s[idx] already exists or not*/ if (tree[tmp].insertEdg[s[idx]- 'a' ] != 0) { // s[idx] X s[idx] already exists in the tree currNode = tree[tmp].insertEdg[s[idx]- 'a' ]; return ; } // creating new Node ptr++; // making new Node as child of X with // weight as s[idx] tree[tmp].insertEdg[s[idx]- 'a' ] = ptr; // calculating length of new Node tree[ptr].length = tree[tmp].length + 2; // updating end point for new Node tree[ptr].end = idx; // updating the start for new Node tree[ptr].start = idx - tree[ptr].length + 1; //STEP 2// /* Setting the suffix edge for the newly created Node tree[ptr]. Finding some String Y such that s[idx] + Y + s[idx] is longest possible palindromic suffix for newly created Node.*/ tmp = tree[tmp].suffixEdg; // making new Node as current Node currNode = ptr; if (tree[currNode].length == 1) { // if new palindrome's length is 1 // making its suffix link to be null string tree[currNode].suffixEdg = 2; return ; } while ( true ) { int curLength = tree[tmp].length; if (idx-curLength >= 1 and s[idx] == s[idx-curLength-1]) break ; tmp = tree[tmp].suffixEdg; } // Now we have found string Y // linking current Nodes suffix link with s[idx]+Y+s[idx] tree[currNode].suffixEdg = tree[tmp].insertEdg[s[idx]- 'a' ]; } // driver program int main() { // initializing the tree root1.length = -1; root1.suffixEdg = 1; root2.length = 0; root2.suffixEdg = 1; tree[1] = root1; tree[2] = root2; ptr = 2; currNode = 1; // given string s = "abcbab" ; int l = s.length(); for ( int i=0; i<l; i++) insert(i); // printing all of its distinct palindromic // substring cout << "All distinct palindromic substring for " << s << " : " ; for ( int i=3; i<=ptr; i++) { cout << i-2 << ") " ; for ( int j=tree[i].start; j<=tree[i].end; j++) cout << s[j]; cout << endl; } return 0; } |
输出:
All distinct palindromic substring for abcbab : 1)a 2)b 3)c 4)bcb 5)abcba 6)bab
时间复杂性 建造过程的时间复杂性将是 O(k*n) “这里” N “是字符串的长度,并且” K ‘是每次插入字符时在后缀链接中查找字符串X和字符串Y所需的额外迭代次数。让我们试着近似常数“k”。我们将考虑最坏的情况。 s=“aaaaaa bcccdeeeef” .在这种情况下,对于连续字符的类似条纹,每个索引需要额外2次迭代才能在后缀链接中找到字符串X和Y,但一旦它达到某个索引 我 这就是我=s[i-1]最大长度后缀的最左边指针将达到其最右边的限制。因此,尽管我 s[我]=s[i-1] ,它将花费总共n次迭代(每次迭代求和),对于剩余的i,当s[i]==s[i-1]时,需要2次迭代,对所有这样的i求和,需要2*n次迭代。因此,在这种情况下,我们的复杂性大约为O(3*n)~O(n)。所以,我们可以粗略地说,常数因子‘k’将非常小。因此,我们可以认为整体的复杂性是线性的。 O(线的长度) 。为了更好地理解,您可以参考参考链接。
参考资料:
本文由 尼蒂什·库马尔 .如果你喜欢GeekSforgek并想投稿,你也可以使用“投稿”撰写文章。极客。组织或邮寄你的文章到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。




![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



