给定一棵具有N个节点(和N-1条边)的无向连通树,我们需要在这棵树中找到两条不相交且其长度乘积最大的路径。
null
例如:
In first tree two paths which are non-intersecting and have highest product are, 1-2 and 3-4, so answer is 1*1 = 1 In second tree two paths which are non-intersecting and has highest product are, 1-3-5 and 7-8-6-2 (or 4-8-6-2), so answer is 3*2 = 6
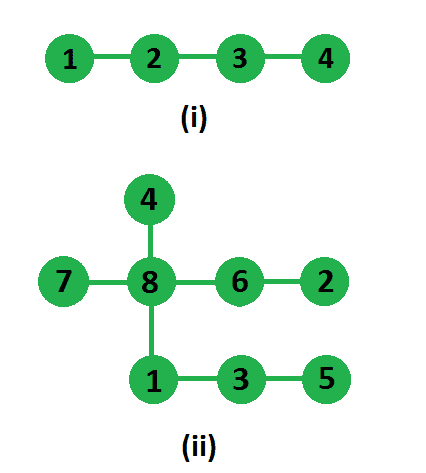
我们可以通过以下步骤通过树的深度优先搜索来解决这个问题,因为树是连接的,路径是不相交的,如果我们选择任何一对这样的路径,必须有第三条路径,连接这两条路径,如果我们从第三条路径移除一条边,那么树将被分成两个部分——一个包含第一条路径,另一个包含第二条路径。这一观察结果为我们提供了一种算法:迭代边缘;对于每条边,删除它,在两个连接的组件中找到路径的长度,并将这些路径的长度相乘。树中路径的长度可以通过修改的深度优先搜索找到,我们将在每个邻居处调用最大路径,并将返回的两个最大长度相加,这将是当前节点上的子树的最大路径长度。
实施细节: 输入是一棵树,但其中没有指定的根,因为我们只有边的集合。树被表示为无向图。我们遍历邻接列表。对于每条边,我们都会在其两侧找到最大长度的路径(删除边后)。我们跟踪因边缘去除而产生的最大产量。
C++
// C++ program to find maximum product of two // non-intersecting paths #include <bits/stdc++.h> using namespace std; /* Returns maximum length path in subtree rooted at u after removing edge connecting u and v */ int dfs(vector< int > g[], int & curMax, int u, int v) { // To find lengths of first and second maximum // in subtrees. currMax is to store overall // maximum. int max1 = 0, max2 = 0, total = 0; // loop through all neighbors of u for ( int i = 0; i < g[u].size(); i++) { // if neighbor is v, then skip it if (g[u][i] == v) continue ; // call recursively with current neighbor as root total = max(total, dfs(g, curMax, g[u][i], u)); // get max from one side and update if (curMax > max1) { max2 = max1; max1 = curMax; } else max2 = max(max2, curMax); } // store total length by adding max // and second max total = max(total, max1 + max2); // update current max by adding 1, i.e. // current node is included curMax = max1 + 1; return total; } // method returns maximum product of length of // two non-intersecting paths int maxProductOfTwoPaths(vector< int > g[], int N) { int res = INT_MIN; int path1, path2; // one by one removing all edges and calling // dfs on both subtrees for ( int i = 1; i < N+2; i++) { for ( int j = 0; j < g[i].size(); j++) { // calling dfs on subtree rooted at // g[i][j], excluding edge from g[i][j] // to i. int curMax = 0; path1 = dfs(g, curMax, g[i][j], i); // calling dfs on subtree rooted at // i, edge from i to g[i][j] curMax = 0; path2 = dfs(g, curMax, i, g[i][j]); res = max(res, path1 * path2); } } return res; } // Utility function to add an undirected edge (u,v) void addEdge(vector< int > g[], int u, int v) { g[u].push_back(v); g[v].push_back(u); } // Driver code to test above methods int main() { int edges[][2] = {{1, 8}, {2, 6}, {3, 1}, {5, 3}, {7, 8}, {8, 4}, {8, 6} }; int N = sizeof (edges)/ sizeof (edges[0]); // there are N edges, so +1 for nodes and +1 // for 1-based indexing vector< int > g[N + 2]; for ( int i = 0; i < N; i++) addEdge(g, edges[i][0], edges[i][1]); cout << maxProductOfTwoPaths(g, N) << endl; return 0; } |
JAVA
// Java program to find maximum product // of two non-intersecting paths import java.util.*; class GFG{ static int curMax; // Returns maximum length path in // subtree rooted at u after // removing edge connecting u and v static int dfs(Vector<Integer> g[], int u, int v) { // To find lengths of first and // second maximum in subtrees. // currMax is to store overall // maximum. int max1 = 0 , max2 = 0 , total = 0 ; // Loop through all neighbors of u for ( int i = 0 ; i < g[u].size(); i++) { // If neighbor is v, then skip it if (g[u].get(i) == v) continue ; // Call recursively with current // neighbor as root total = Math.max(total, dfs( g, g[u].get(i), u)); // Get max from one side and update if (curMax > max1) { max2 = max1; max1 = curMax; } else max2 = Math.max(max2, curMax); } // Store total length by adding max // and second max total = Math.max(total, max1 + max2); // Update current max by adding 1, i.e. // current node is included curMax = max1 + 1 ; return total; } // Method returns maximum product of // length of two non-intersecting paths static int maxProductOfTwoPaths(Vector<Integer> g[], int N) { int res = Integer.MIN_VALUE; int path1, path2; // One by one removing all edges and // calling dfs on both subtrees for ( int i = 1 ; i < N + 2 ; i++) { for ( int j = 0 ; j < g[i].size(); j++) { // Calling dfs on subtree rooted at // g[i][j], excluding edge from g[i][j] // to i. curMax = 0 ; path1 = dfs(g, g[i].get(j), i); // Calling dfs on subtree rooted at // i, edge from i to g[i][j] curMax = 0 ; path2 = dfs(g,i, g[i].get(j)); res = Math.max(res, path1 * path2); } } return res; } // Utility function to add an // undirected edge (u,v) static void addEdge(Vector<Integer> g[], int u, int v) { g[u].add(v); g[v].add(u); } // Driver code public static void main(String[] args) { int edges[][] = { { 1 , 8 }, { 2 , 6 }, { 3 , 1 }, { 5 , 3 }, { 7 , 8 }, { 8 , 4 }, { 8 , 6 } }; int N = edges.length; // There are N edges, so +1 for nodes // and +1 for 1-based indexing @SuppressWarnings ( "unchecked" ) Vector<Integer> []g = new Vector[N + 2 ]; for ( int i = 0 ; i < g.length; i++) g[i] = new Vector<Integer>(); for ( int i = 0 ; i < N; i++) addEdge(g, edges[i][ 0 ], edges[i][ 1 ]); System.out.print(maxProductOfTwoPaths(g, N) + "" ); } } // This code is contributed by Princi Singh |
Python3
# Python3 program to find maximum product of two # non-intersecting paths # Returns maximum length path in subtree rooted # at u after removing edge connecting u and v def dfs(g, curMax, u, v): # To find lengths of first and second maximum # in subtrees. currMax is to store overall # maximum. max1 = 0 max2 = 0 total = 0 # loop through all neighbors of u for i in range ( len (g[u])): # if neighbor is v, then skip it if (g[u][i] = = v): continue # call recursively with current neighbor as root total = max (total, dfs(g, curMax, g[u][i], u)) # get max from one side and update if (curMax[ 0 ] > max1): max2 = max1 max1 = curMax[ 0 ] else : max2 = max (max2, curMax[ 0 ]) # store total length by adding max # and second max total = max (total, max1 + max2) # update current max by adding 1, i.e. # current node is included curMax[ 0 ] = max1 + 1 return total # method returns maximum product of length of # two non-intersecting paths def maxProductOfTwoPaths(g, N): res = - 999999999999 path1, path2 = None , None # one by one removing all edges and calling # dfs on both subtrees for i in range (N): for j in range ( len (g[i])): # calling dfs on subtree rooted at # g[i][j], excluding edge from g[i][j] # to i. curMax = [ 0 ] path1 = dfs(g, curMax, g[i][j], i) # calling dfs on subtree rooted at # i, edge from i to g[i][j] curMax = [ 0 ] path2 = dfs(g, curMax, i, g[i][j]) res = max (res, path1 * path2) return res # Utility function to add an undirected edge (u,v) def addEdge(g, u, v): g[u].append(v) g[v].append(u) # Driver code if __name__ = = '__main__' : edges = [[ 1 , 8 ], [ 2 , 6 ], [ 3 , 1 ], [ 5 , 3 ], [ 7 , 8 ], [ 8 , 4 ], [ 8 , 6 ]] N = len (edges) # there are N edges, so +1 for nodes and +1 # for 1-based indexing g = [[] for i in range (N + 2 )] for i in range (N): addEdge(g, edges[i][ 0 ], edges[i][ 1 ]) print (maxProductOfTwoPaths(g, N)) # This code is contributed by PranchalK |
C#
// C# program to find maximum product // of two non-intersecting paths using System; using System.Collections.Generic; public class GFG { static int curMax; // Returns maximum length path in // subtree rooted at u after // removing edge connecting u and v static int dfs(List< int > []g, int u, int v) { // To find lengths of first and // second maximum in subtrees. // currMax is to store overall // maximum. int max1 = 0, max2 = 0, total = 0; // Loop through all neighbors of u for ( int i = 0; i < g[u].Count; i++) { // If neighbor is v, then skip it if (g[u][i] == v) continue ; // Call recursively with current // neighbor as root total = Math.Max(total, dfs( g, g[u][i], u)); // Get max from one side and update if (curMax > max1) { max2 = max1; max1 = curMax; } else max2 = Math.Max(max2, curMax); } // Store total length by adding max // and second max total = Math.Max(total, max1 + max2); // Update current max by adding 1, i.e. // current node is included curMax = max1 + 1; return total; } // Method returns maximum product of // length of two non-intersecting paths static int maxProductOfTwoPaths(List< int > []g, int N) { int res = int .MinValue; int path1, path2; // One by one removing all edges and // calling dfs on both subtrees for ( int i = 1; i < N + 2; i++) { for ( int j = 0; j < g[i].Count; j++) { // Calling dfs on subtree rooted at // g[i,j], excluding edge from g[i,j] // to i. curMax = 0; path1 = dfs(g, g[i][j], i); // Calling dfs on subtree rooted at // i, edge from i to g[i,j] curMax = 0; path2 = dfs(g,i, g[i][j]); res = Math.Max(res, path1 * path2); } } return res; } // Utility function to add an // undirected edge (u,v) static void addEdge(List< int > []g, int u, int v) { g[u].Add(v); g[v].Add(u); } // Driver code public static void Main(String[] args) { int [,]edges = { { 1, 8 }, { 2, 6 }, { 3, 1 }, { 5, 3 }, { 7, 8 }, { 8, 4 }, { 8, 6 } }; int N = edges.GetLength(0); // There are N edges, so +1 for nodes // and +1 for 1-based indexing List< int > []g = new List< int >[N + 2]; for ( int i = 0; i < g.Length; i++) g[i] = new List< int >(); for ( int i = 0; i < N; i++) addEdge(g, edges[i,0], edges[i,1]); Console.Write(maxProductOfTwoPaths(g, N) + "" ); } } // This code is contributed by aashish1995 |
Javascript
<script> // Javascript program to find maximum product of two // non-intersecting paths let curMax; // Returns maximum length path in // subtree rooted at u after // removing edge connecting u and v function dfs(g, u, v) { // To find lengths of first and // second maximum in subtrees. // currMax is to store overall // maximum. let max1 = 0, max2 = 0, total = 0; // Loop through all neighbors of u for (let i = 0; i < g[u].length; i++) { // If neighbor is v, then skip it if (g[u][i] == v) continue ; // Call recursively with current // neighbor as root total = Math.max(total, dfs( g, g[u][i], u)); // Get max from one side and update if (curMax > max1) { max2 = max1; max1 = curMax; } else max2 = Math.max(max2, curMax); } // Store total length by adding max // and second max total = Math.max(total, max1 + max2); // Update current max by adding 1, i.e. // current node is included curMax = max1 + 1; return total; } // Method returns maximum product of // length of two non-intersecting paths function maxProductOfTwoPaths(g, N) { let res = Number.MIN_VALUE; let path1, path2; // One by one removing all edges and // calling dfs on both subtrees for (let i = 1; i < N + 2; i++) { for (let j = 0; j < g[i].length; j++) { // Calling dfs on subtree rooted at // g[i,j], excluding edge from g[i,j] // to i. curMax = 0; path1 = dfs(g, g[i][j], i); // Calling dfs on subtree rooted at // i, edge from i to g[i,j] curMax = 0; path2 = dfs(g,i, g[i][j]); res = Math.max(res, path1 * path2); } } return res; } // Utility function to add an // undirected edge (u,v) function addEdge(g, u, v) { g[u].push(v); g[v].push(u); } let edges = [ [ 1, 8 ], [ 2, 6 ], [ 3, 1 ], [ 5, 3 ], [ 7, 8 ], [ 8, 4 ], [ 8, 6 ] ]; let N = edges.length; // There are N edges, so +1 for nodes // and +1 for 1-based indexing let g = []; for (let i = 0; i < N + 2; i++) { g.push([]); } for (let i = 0; i < g.length; i++) g[i] = []; for (let i = 0; i < N; i++) addEdge(g, edges[i][0], edges[i][1]); document.write(maxProductOfTwoPaths(g, N) + "</br>" ); // This code is contributed by divyesh072019. </script> |
输出:
6
本文由 乌特卡什·特里维迪 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



