给定一个无向图的邻接表表示。编写一个函数来计算无向图中的边数。
null
预期时间复杂度:O(V)
例如:
Input : Adjacency list representation of
below graph.
Output : 9
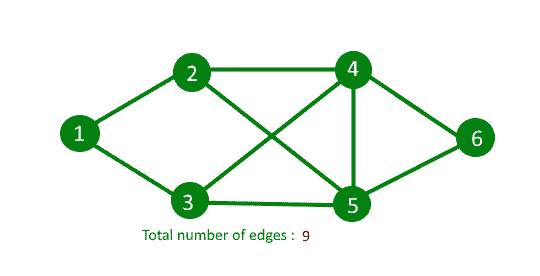
这个想法基于握手引理。 握手引理 是关于无向图的。在每一个有限无向图中,奇数次顶点的数目总是偶数。握手引理是度和公式的结果(有时也称为握手引理)
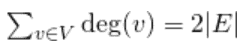
所以我们遍历所有顶点,计算它们的邻接列表的大小之和,最后返回sum/2。下面是上述想法的实现
C++
// C++ program to count number of edge in // undirected graph #include<bits/stdc++.h> using namespace std; // Adjacency list representation of graph class Graph { int V ; list < int > *adj; public : Graph( int V ) { this ->V = V ; adj = new list< int >[V]; } void addEdge ( int u, int v ) ; int countEdges () ; }; // add edge to graph void Graph :: addEdge ( int u, int v ) { adj[u].push_back(v); adj[v].push_back(u); } // Returns count of edge in undirected graph int Graph :: countEdges() { int sum = 0; //traverse all vertex for ( int i = 0 ; i < V ; i++) // add all edge that are linked to the // current vertex sum += adj[i].size(); // The count of edge is always even because in // undirected graph every edge is connected // twice between two vertices return sum/2; } // driver program to check above function int main() { int V = 9 ; Graph g(V); // making above uhown graph g.addEdge(0, 1 ); g.addEdge(0, 7 ); g.addEdge(1, 2 ); g.addEdge(1, 7 ); g.addEdge(2, 3 ); g.addEdge(2, 8 ); g.addEdge(2, 5 ); g.addEdge(3, 4 ); g.addEdge(3, 5 ); g.addEdge(4, 5 ); g.addEdge(5, 6 ); g.addEdge(6, 7 ); g.addEdge(6, 8 ); g.addEdge(7, 8 ); cout << g.countEdges() << endl; return 0; } |
JAVA
// Java program to count number of edge in // undirected graph import java.io.*; import java.util.*; // Adjacency list representation of graph class Graph { int V; Vector<Integer>[] adj; //@SuppressWarnings("unchecked") Graph( int V) { this .V = V; this .adj = new Vector[V]; for ( int i = 0 ; i < V; i++) adj[i] = new Vector<Integer>(); } // add edge to graph void addEdge( int u, int v) { adj[u].add(v); adj[v].add(u); } // Returns count of edge in undirected graph int countEdges() { int sum = 0 ; // traverse all vertex for ( int i = 0 ; i < V; i++) // add all edge that are linked to the // current vertex sum += adj[i].size(); // The count of edge is always even because in // undirected graph every edge is connected // twice between two vertices return sum / 2 ; } } class GFG { // Driver Code public static void main(String[] args) throws IOException { int V = 9 ; Graph g = new Graph(V); // making above uhown graph g.addEdge( 0 , 1 ); g.addEdge( 0 , 7 ); g.addEdge( 1 , 2 ); g.addEdge( 1 , 7 ); g.addEdge( 2 , 3 ); g.addEdge( 2 , 8 ); g.addEdge( 2 , 5 ); g.addEdge( 3 , 4 ); g.addEdge( 3 , 5 ); g.addEdge( 4 , 5 ); g.addEdge( 5 , 6 ); g.addEdge( 6 , 7 ); g.addEdge( 6 , 8 ); g.addEdge( 7 , 8 ); System.out.println(g.countEdges()); } } // This code is contributed by // sanjeev2552 |
Python3
# Python3 program to count number of # edge in undirected graph # Adjacency list representation of graph class Graph: def __init__( self , V): self .V = V self .adj = [[] for i in range (V)] # add edge to graph def addEdge ( self , u, v ): self .adj[u].append(v) self .adj[v].append(u) # Returns count of edge in undirected graph def countEdges( self ): Sum = 0 # traverse all vertex for i in range ( self .V): # add all edge that are linked # to the current vertex Sum + = len ( self .adj[i]) # The count of edge is always even # because in undirected graph every edge # is connected twice between two vertices return Sum / / 2 # Driver Code if __name__ = = '__main__' : V = 9 g = Graph(V) # making above uhown graph g.addEdge( 0 , 1 ) g.addEdge( 0 , 7 ) g.addEdge( 1 , 2 ) g.addEdge( 1 , 7 ) g.addEdge( 2 , 3 ) g.addEdge( 2 , 8 ) g.addEdge( 2 , 5 ) g.addEdge( 3 , 4 ) g.addEdge( 3 , 5 ) g.addEdge( 4 , 5 ) g.addEdge( 5 , 6 ) g.addEdge( 6 , 7 ) g.addEdge( 6 , 8 ) g.addEdge( 7 , 8 ) print (g.countEdges()) # This code is contributed by PranchalK |
C#
// C# program to count number of edge in // undirected graph using System; using System.Collections.Generic; // Adjacency list representation of graph class Graph { public int V; public List< int >[] adj; public Graph( int V) { this .V = V; this .adj = new List< int >[V]; for ( int i = 0; i < V; i++) adj[i] = new List< int >(); } // add edge to graph public void addEdge( int u, int v) { adj[u].Add(v); adj[v].Add(u); } // Returns count of edge in undirected graph public int countEdges() { int sum = 0; // traverse all vertex for ( int i = 0; i < V; i++) // add all edge that are linked to the // current vertex sum += adj[i].Count; // The count of edge is always even because in // undirected graph every edge is connected // twice between two vertices return sum / 2; } } class GFG { // Driver Code public static void Main(String[] args) { int V = 9; Graph g = new Graph(V); // making above uhown graph g.addEdge(0, 1); g.addEdge(0, 7); g.addEdge(1, 2); g.addEdge(1, 7); g.addEdge(2, 3); g.addEdge(2, 8); g.addEdge(2, 5); g.addEdge(3, 4); g.addEdge(3, 5); g.addEdge(4, 5); g.addEdge(5, 6); g.addEdge(6, 7); g.addEdge(6, 8); g.addEdge(7, 8); Console.WriteLine(g.countEdges()); } } // This code is contributed by PrinciRaj1992 |
输出:
14
时间复杂性: O(V)
本文由 尼桑·辛格 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 贡献极客。组织 或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



