给定一个长度为n的小写字母字符串,我们需要计算该字符串的不同子字符串的总数。 例如:
null
Input : str = “ababa” Output : 10 Total number of distinct substring are 10, which are, "", "a", "b", "ab", "ba", "aba", "bab", "abab", "baba" and "ababa"
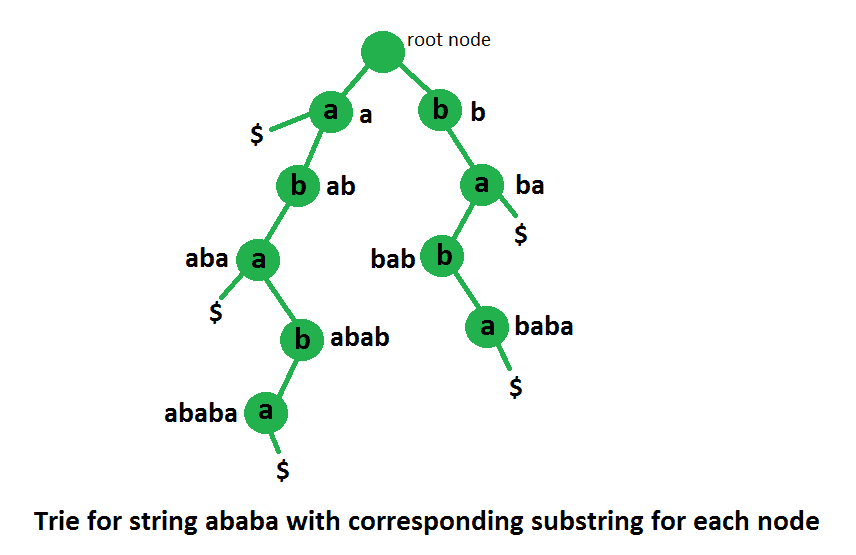
这个想法是创造一个 所有后缀中的Trie 给定字符串的。一旦Trie被压缩,我们的答案就是构造的Trie中的节点总数。例如,下图代表了“ababa”所有后缀的Trie。节点总数是10,这是我们的答案。
这是怎么回事?
- 每个根到节点的路径 崔 表示Trie中存在的单词的前缀。在这里,我们说的是后缀。所以每个节点代表一个后缀前缀。
- 字符串“str”的每个子字符串都是“str”后缀的前缀。
下面是基于上述思想的实现。
C++
// A C++ program to find the count of distinct substring // of a string using trie data structure #include <bits/stdc++.h> #define MAX_CHAR 26 using namespace std; // A Suffix Trie (A Trie of all suffixes) Node class SuffixTrieNode { public : SuffixTrieNode *children[MAX_CHAR]; SuffixTrieNode() // Constructor { // Initialize all child pointers as NULL for ( int i = 0; i < MAX_CHAR; i++) children[i] = NULL; } // A recursive function to insert a suffix of the s // in subtree rooted with this node void insertSuffix(string suffix); }; // A Trie of all suffixes class SuffixTrie { SuffixTrieNode *root; int _countNodesInTrie(SuffixTrieNode *); public : // Constructor (Builds a trie of suffies of the given text) SuffixTrie(string s) { root = new SuffixTrieNode(); // Consider all suffixes of given string and insert // them into the Suffix Trie using recursive function // insertSuffix() in SuffixTrieNode class for ( int i = 0; i < s.length(); i++) root->insertSuffix(s.substr(i)); } // method to count total nodes in suffix trie int countNodesInTrie() { return _countNodesInTrie(root); } }; // A recursive function to insert a suffix of the s in // subtree rooted with this node void SuffixTrieNode::insertSuffix(string s) { // If string has more characters if (s.length() > 0) { // Find the first character and convert it // into 0-25 range. char cIndex = s.at(0) - 'a' ; // If there is no edge for this character, // add a new edge if (children[cIndex] == NULL) children[cIndex] = new SuffixTrieNode(); // Recur for next suffix children[cIndex]->insertSuffix(s.substr(1)); } } // A recursive function to count nodes in trie int SuffixTrie::_countNodesInTrie(SuffixTrieNode* node) { // If all characters of pattern have been processed, if (node == NULL) return 0; int count = 0; for ( int i = 0; i < MAX_CHAR; i++) { // if children is not NULL then find count // of all nodes in this subtrie if (node->children[i] != NULL) count += _countNodesInTrie(node->children[i]); } // return count of nodes of subtrie and plus // 1 because of node's own count return (1 + count); } // Returns count of distinct substrings of str int countDistinctSubstring(string str) { // Construct a Trie of all suffixes SuffixTrie sTrie(str); // Return count of nodes in Trie of Suffixes return sTrie.countNodesInTrie(); } // Driver program to test above function int main() { string str = "ababa" ; cout << "Count of distinct substrings is " << countDistinctSubstring(str); return 0; } |
JAVA
// A Java program to find the count of distinct substring // of a string using trie data structure public class Suffix { // A Suffix Trie (A Trie of all suffixes) Node static class SuffixTrieNode { static final int MAX_CHAR = 26 ; SuffixTrieNode[] children = new SuffixTrieNode[MAX_CHAR]; SuffixTrieNode() // Constructor { // Initialize all child pointers as NULL for ( int i = 0 ; i < MAX_CHAR; i++) children[i] = null ; } // A recursive function to insert a suffix of the s in // subtree rooted with this node void insertSuffix(String s) { // If string has more characters if (s.length() > 0 ) { // Find the first character and convert it // into 0-25 range. char cIndex = ( char ) (s.charAt( 0 ) - 'a' ); // If there is no edge for this character, // add a new edge if (children[cIndex] == null ) children[cIndex] = new SuffixTrieNode(); // Recur for next suffix children[cIndex].insertSuffix(s.substring( 1 )); } } } // A Trie of all suffixes static class Suffix_trie { static final int MAX_CHAR = 26 ; SuffixTrieNode root; // Constructor (Builds a trie of suffies of the given text) Suffix_trie(String s) { root = new SuffixTrieNode(); // Consider all suffixes of given string and insert // them into the Suffix Trie using recursive function // insertSuffix() in SuffixTrieNode class for ( int i = 0 ; i < s.length(); i++) root.insertSuffix(s.substring(i)); } // A recursive function to count nodes in trie int _countNodesInTrie(SuffixTrieNode node) { // If all characters of pattern have been processed, if (node == null ) return 0 ; int count = 0 ; for ( int i = 0 ; i < MAX_CHAR; i++) { // if children is not NULL then find count // of all nodes in this subtrie if (node.children[i] != null ) count += _countNodesInTrie(node.children[i]); } // return count of nodes of subtrie and plus // 1 because of node's own count return ( 1 + count); } // method to count total nodes in suffix trie int countNodesInTrie() { return _countNodesInTrie(root); } } // Returns count of distinct substrings of str static int countDistinctSubstring(String str) { // Construct a Trie of all suffixes Suffix_trie sTrie = new Suffix_trie(str); // Return count of nodes in Trie of Suffixes return sTrie.countNodesInTrie(); } // Driver program to test above function public static void main(String args[]) { String str = "ababa" ; System.out.println( "Count of distinct substrings is " + countDistinctSubstring(str)); } } // This code is contributed by Sumit Ghosh |
C#
// C# program to find the count of distinct substring // of a string using trie data structure using System; public class Suffix { // A Suffix Trie (A Trie of all suffixes) Node public class SuffixTrieNode { static readonly int MAX_CHAR = 26; public SuffixTrieNode[] children = new SuffixTrieNode[MAX_CHAR]; public SuffixTrieNode() // Constructor { // Initialize all child pointers as NULL for ( int i = 0; i < MAX_CHAR; i++) children[i] = null ; } // A recursive function to insert a suffix of the s in // subtree rooted with this node public void insertSuffix(String s) { // If string has more characters if (s.Length > 0) { // Find the first character and convert it // into 0-25 range. char cIndex = ( char ) (s[0] - 'a' ); // If there is no edge for this character, // add a new edge if (children[cIndex] == null ) children[cIndex] = new SuffixTrieNode(); // Recur for next suffix children[cIndex].insertSuffix(s.Substring(1)); } } } // A Trie of all suffixes public class Suffix_trie { static readonly int MAX_CHAR = 26; public SuffixTrieNode root; // Constructor (Builds a trie of suffies of the given text) public Suffix_trie(String s) { root = new SuffixTrieNode(); // Consider all suffixes of given string and insert // them into the Suffix Trie using recursive function // insertSuffix() in SuffixTrieNode class for ( int i = 0; i < s.Length; i++) root.insertSuffix(s.Substring(i)); } // A recursive function to count nodes in trie public int _countNodesInTrie(SuffixTrieNode node) { // If all characters of pattern have been processed, if (node == null ) return 0; int count = 0; for ( int i = 0; i < MAX_CHAR; i++) { // if children is not NULL then find count // of all nodes in this subtrie if (node.children[i] != null ) count += _countNodesInTrie(node.children[i]); } // return count of nodes of subtrie and plus // 1 because of node's own count return (1 + count); } // method to count total nodes in suffix trie public int countNodesInTrie() { return _countNodesInTrie(root); } } // Returns count of distinct substrings of str static int countDistinctSubstring(String str) { // Construct a Trie of all suffixes Suffix_trie sTrie = new Suffix_trie(str); // Return count of nodes in Trie of Suffixes return sTrie.countNodesInTrie(); } // Driver program to test above function public static void Main(String []args) { String str = "ababa" ; Console.WriteLine( "Count of distinct substrings is " + countDistinctSubstring(str)); } } // This code contributed by Rajput-Ji |
输出:
Count of distinct substrings is 10
本文由 乌特卡什·特里维迪 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 贡献极客。组织 或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



