遍历图形有两种常见方法, BFS 和 DFS .考虑到一棵高度和宽度都很大的树(或图形),BFS和DFS都不是很有效,原因如下。
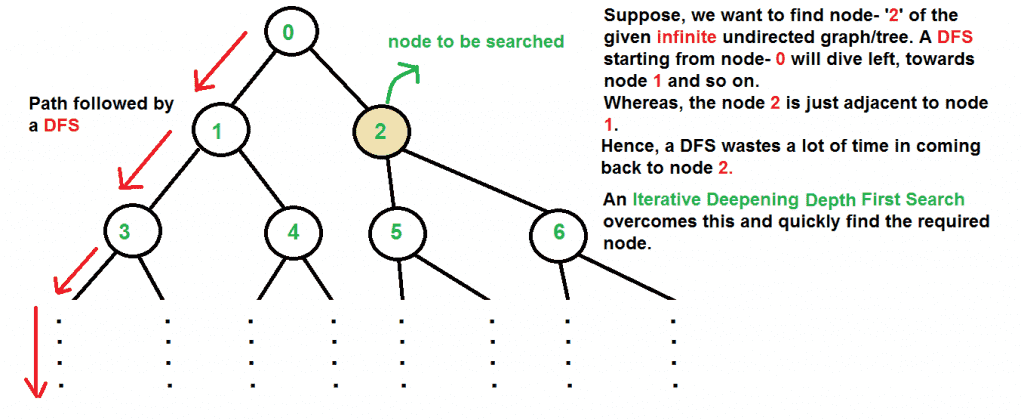
- DFS 首先遍历通过根的一个相邻节点,然后遍历下一个相邻节点。这种方法的问题是,如果有一个节点靠近根,但不在DFS探索的前几个子树中,那么DFS到达该节点的时间很晚。此外,DFS可能无法找到到节点的最短路径(根据边的数量)。
- BFS 逐级进行,但需要更多的空间。DFS所需的空间是O(d),其中d是树的深度,而BFS所需的空间是O(n),其中n是树中的节点数(为什么?请注意,树的最后一级可以有大约n/2个节点,第二级可以有n/4个节点,在BFS中,我们需要让每一级逐个排队)。
IDDFS 结合了深度优先搜索的空间效率和广度优先搜索的快速搜索(用于更接近根的节点)。
IDDF是如何工作的? IDDFS从初始值开始调用不同深度的DFS。在每次通话中,DFS都被限制在给定深度之外。所以基本上我们用BFS的方式做DFS。
算法:
// Returns true if target is reachable from
// src within max_depth
bool IDDFS(src, target, max_depth)
for limit from 0 to max_depth
if DLS(src, target, limit) == true
return true
return false
bool DLS(src, target, limit)
if (src == target)
return true;
// If reached the maximum depth,
// stop recursing.
if (limit <= 0)
return false;
foreach adjacent i of src
if DLS(i, target, limit?1)
return true
return false
需要注意的一点是,我们多次访问顶级节点。最后一级(或最大深度)访问一次,第二级访问两次,依此类推。它可能看起来很昂贵,但事实证明并没有那么昂贵,因为在树中,大多数节点都位于底层。因此,如果高层被多次访问,也没什么大不了的。
下面是上述算法的实现
C/C++
// C++ program to search if a target node is reachable from // a source with given max depth. #include<bits/stdc++.h> using namespace std; // Graph class represents a directed graph using adjacency // list representation. class Graph { int V; // No. of vertices // Pointer to an array containing // adjacency lists list< int > *adj; // A function used by IDDFS bool DLS( int v, int target, int limit); public : Graph( int V); // Constructor void addEdge( int v, int w); // IDDFS traversal of the vertices reachable from v bool IDDFS( int v, int target, int max_depth); }; Graph::Graph( int V) { this ->V = V; adj = new list< int >[V]; } void Graph::addEdge( int v, int w) { adj[v].push_back(w); // Add w to v’s list. } // A function to perform a Depth-Limited search // from given source 'src' bool Graph::DLS( int src, int target, int limit) { if (src == target) return true ; // If reached the maximum depth, stop recursing. if (limit <= 0) return false ; // Recur for all the vertices adjacent to source vertex for ( auto i = adj[src].begin(); i != adj[src].end(); ++i) if (DLS(*i, target, limit-1) == true ) return true ; return false ; } // IDDFS to search if target is reachable from v. // It uses recursive DFSUtil(). bool Graph::IDDFS( int src, int target, int max_depth) { // Repeatedly depth-limit search till the // maximum depth. for ( int i = 0; i <= max_depth; i++) if (DLS(src, target, i) == true ) return true ; return false ; } // Driver code int main() { // Let us create a Directed graph with 7 nodes Graph g(7); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 3); g.addEdge(1, 4); g.addEdge(2, 5); g.addEdge(2, 6); int target = 6, maxDepth = 3, src = 0; if (g.IDDFS(src, target, maxDepth) == true ) cout << "Target is reachable from source " "within max depth" ; else cout << "Target is NOT reachable from source " "within max depth" ; return 0; } |
python
# Python program to print DFS traversal from a given # given graph from collections import defaultdict # This class represents a directed graph using adjacency # list representation class Graph: def __init__( self ,vertices): # No. of vertices self .V = vertices # default dictionary to store graph self .graph = defaultdict( list ) # function to add an edge to graph def addEdge( self ,u,v): self .graph[u].append(v) # A function to perform a Depth-Limited search # from given source 'src' def DLS( self ,src,target,maxDepth): if src = = target : return True # If reached the maximum depth, stop recursing. if maxDepth < = 0 : return False # Recur for all the vertices adjacent to this vertex for i in self .graph[src]: if ( self .DLS(i,target,maxDepth - 1 )): return True return False # IDDFS to search if target is reachable from v. # It uses recursive DLS() def IDDFS( self ,src, target, maxDepth): # Repeatedly depth-limit search till the # maximum depth for i in range (maxDepth): if ( self .DLS(src, target, i)): return True return False # Create a graph given in the above diagram g = Graph ( 7 ); g.addEdge( 0 , 1 ) g.addEdge( 0 , 2 ) g.addEdge( 1 , 3 ) g.addEdge( 1 , 4 ) g.addEdge( 2 , 5 ) g.addEdge( 2 , 6 ) target = 6 ; maxDepth = 3 ; src = 0 if g.IDDFS(src, target, maxDepth) = = True : print ( "Target is reachable from source " + "within max depth" ) else : print ( "Target is NOT reachable from source " + "within max depth" ) # This code is contributed by Neelam Pandey |
Target is reachable from source within max depth
插图: 可能有两种情况- a) 当图形没有循环时: 这个案子很简单。我们可以多次使用不同的高度限制。
b) 当图形有循环时。 这很有趣,因为IDDFS中没有访问标志。 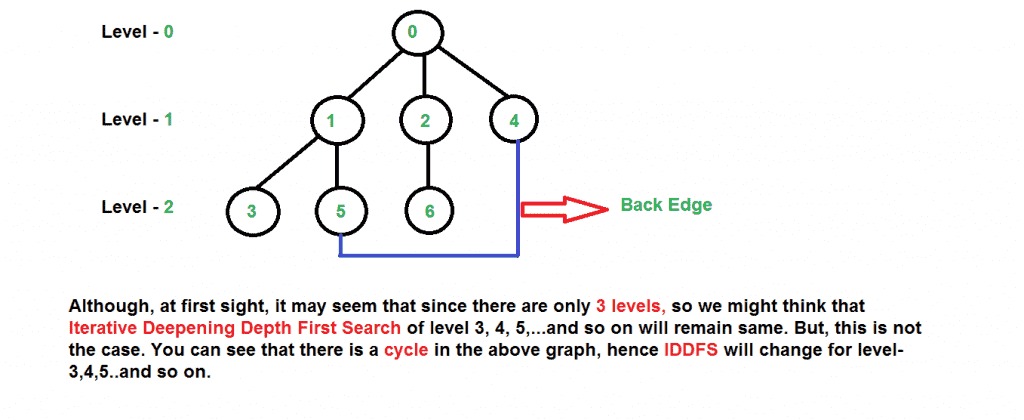
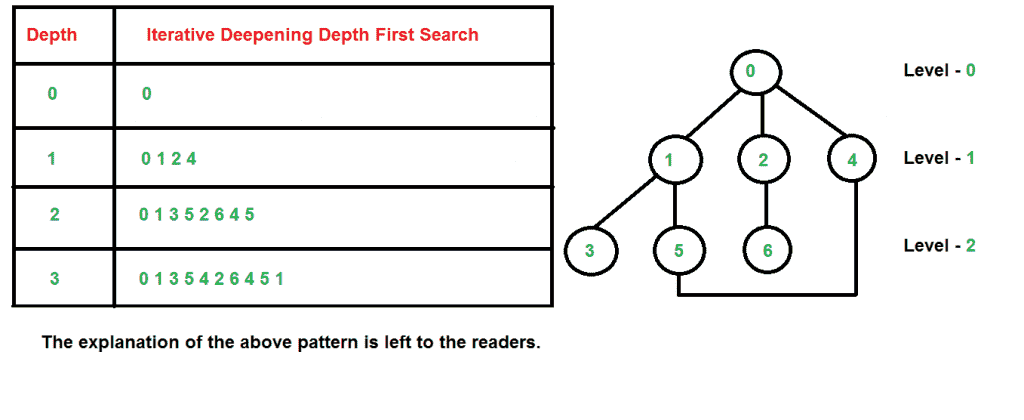
时间复杂性: 假设我们有一棵树,其分支因子为“b”(每个节点的子节点数),其深度为“d”,即 B D 节点。
在迭代深化搜索中,底层上的节点展开一次,底层下一层上的节点展开两次,依此类推,直到搜索树的根,搜索树的根被展开d+1次。所以迭代深化搜索中展开的总数是-
(d)b + (d-1)b2 + .... + 3bd-2 + 2bd-1 + bd That is, Summation[(d + 1 - i) bi], from i = 0 to i = d Which is same as O(bd)
在对上述表达式进行评估后,我们发现渐近IDDF与DFS和BFS的时间相同,但它确实比两者都慢,因为它的时间复杂度表达式中有一个更高的常数因子。
IDDFS最适合于完整的无限树
参考资料: https://en.wikipedia.org/wiki/Iterative_deepening_depth-first_search
本文由 拉希特·贝尔瓦里亚 .如果你喜欢GeekSforgek,并且想贡献自己的力量,你也可以写一篇文章,并将文章邮寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论



![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



