检查一个数字是否可以表示为连续数字的总和-yiteyi-C++库

给定一个数字n，任务是检查它是否可以表示为两个或多个连续数字的和。例如：

null

Input  : n = 10 
Output : true
It can be expressed as sum of two consecutive
numbers 1 + 2 + 3 + 4.

Input  : n = 16  
Output : false
It cannot be expressed as sum of two consecutive
numbers.

Input  : n = 5  
Output : true
2 + 3 = 5

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

有一种直接而快速的方法可以解决这个问题。如果一个数是二的幂，那么它不能表示为连续数的和，否则是的。这个想法基于以下两个事实。 1）任意两个连续数之和都是奇数，因为其中一个数必须是偶数，另一个数必须是奇数。 2) 2 ^N = 2 ^n-1 + 2 ^n-1 如果我们仔细观察1）和2），我们可以得到事实背后的直觉。下面是上述想法的实施。

C++

                         // C++ program to check if a number can                       
                         // be expressed as sum of consecutive numbers                       
                         #include<bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
                                   
                         // This function returns true if n can be                       
                         // expressed sum of consecutive.                       
                         bool                                     canBeSumofConsec(unsigned                                     int                                     n)                       
                         {                       
                                                 // We basically return true if n is a                       
                                                 // power of two                       
                                                 return                                     ((n&(n-1)) && n);                       
                         }                       
                                   
                         // Driver code                       
                         int                                     main()                       
                         {                       
                                                 unsigned                                     int                                     n = 15;                       
                                                 canBeSumofConsec(n)? cout <<                                     "true"                                     :                       
                                                 cout <<                                     "false"                                     ;                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to check if a number can                       
                         // be expressed as sum of consecutive numbers                       
                                   
                         class                                     Test                       
                         {                       
                                                 // This function returns true if n can be                       
                                                 // expressed sum of consecutive.                       
                                                 static                                     boolean                                     canBeSumofConsec(                                     int                                     n)                       
                                                 {                       
                                                 // We basically return true if n is a                       
                                                 // power of two                       
                                                 return                                     (((n&(n-                                     1                                     ))!=                                     0                                     ) && n!=                                     0                                     );                       
                                                 }                       
                                   
                                                 // Driver method                       
                                                 public                                     static                                     void                                     main(String[] args)                       
                                                 {                       
                                                 int                                     n =                                     15                                     ;                       
                                                 System.out.println(canBeSumofConsec(n) ?                                     "true"                                     :                                     "false"                                     );                       
                                                 }                       
                         }                       

Python3

                         # Python 3 program to check if a number can                       
                         # be expressed as sum of consecutive numbers                       
                                   
                                   
                         # This function returns true if n                       
                         # can be expressed sum of consecutive.                       
                         def                                     canBeSumofConsec(n) :                       
                                   
                                                 # We basically return true if n is a                       
                                                 # power of two                       
                                                 return                                     ((n&(n                                     -                                     1                                     ))                                     and                                     n)                       
                                   
                                   
                         # Driver code                       
                         n                                     =                                     15                       
                         if                                     (canBeSumofConsec(n)) :                       
                                                 print                                     (                                     "true"                                     )                       
                         else                                     :                       
                                                 print                                     (                                     "false"                                     )                       
                                   
                         # This code is contributed by Nikita Tiwari.                       

C#

                         // C# program to check if a number can be                       
                         // expressed as sum of consecutive numbers                       
                         using                                     System;                       
                                   
                         class                                     Test                       
                         {                       
                                                 // This function returns true if n                       
                                                 // can be expressed sum of consecutive.                       
                                                 static                                     bool                                     canBeSumofConsec(                                     int                                     n)                       
                                                 {                       
                                                 // We basically return true if n is a                       
                                                 // power of two                       
                                                 return                                     (((n & (n - 1)) != 0) && n != 0);                       
                                                 }                       
                                   
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     Main()                       
                                                 {                       
                                                 int                                     n = 15;                       
                                                 Console.Write(canBeSumofConsec(n) ?                                     "True"                                     :                                     "False"                                     );                       
                                                 }                       
                         }                       
                                   
                         // This code is contributed by Nitin Mittal.                       

PHP

                         <?php                       
                         // php program to check if a number                       
                         // can be expressed as sum of                       
                         // consecutive numbers                       
                                   
                         // This function returns true if n                       
                         // can be expressed sum of consecutive.                       
                         function                                     canBeSumofConsec(                                     $n                                     )                       
                         {                       
                                   
                                                 // We basically return true if n is a                       
                                                 // power of two                       
                                                 return                                     ((                                     $n                                     & (                                     $n                                     - 1)) &&                                     $n                                     );                       
                         }                       
                                   
                         // Driver code                       
                                                 $n                                     = 15;                       
                                                 if                                     (canBeSumofConsec(                                     $n                                     ))                       
                                                 echo                                     "true"                                     ;                       
                                                 else                       
                                                 echo                                     "false"                                     ;                       
                                   
                         // This code is contributed by                       
                         // nitin mittal.                       
                         ?>                       

Javascript

                         <script>                       
                                   
                         // Javascript program to check if a number can                       
                         // be expressed as sum of consecutive numbers                       
                                   
                                   
                                                 // This function returns true if n can be                       
                                                 // expressed sum of consecutive.                       
                                                 function                                     canBeSumofConsec(n)                       
                                                 {                       
                                                 // We basically return true if n is a                       
                                                 // power of two                       
                                                 return                                     (((n&(n-1))!=0) && n!=0);                       
                                                 }                       
                                   
                                   
                         // function call                       
                                   
                                                 let n = 15;                       
                                                 document.write(canBeSumofConsec(n) ?                                     "true"                                     :                                     "false"                                     );                       
                                   
                         </script>                       

输出：

True

时间复杂度：O（1）

辅助空间：O（1）

另一种方法：

让被选择来表示N为连续数之和的数为 X+1，X+2，X+3…。Y

这些选定数字的总和= 第一个Y自然数之和–第一个X自然数之和

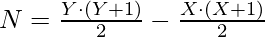
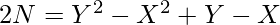
第一个Y自然数之和= $frac {Y cdot (Y + 1)} {2}$ 前X个自然数之和= $frac {X cdot (X + 1)} {2}$ 我们知道， N=第一个Y自然数之和–第一个X自然数之和 $N = frac {Y cdot (Y + 1)} {2} - frac {X cdot (X + 1)} {2}$ $2N = Y cdot (Y + 1) - X cdot (X + 1)$ $2N = Y ^ 2 - X ^ 2 + Y - X$ $2N = (Y - X) cdot (Y + X + 1)$ 设Y-X=a，Y+X+1=b Y+X+1>Y-X，b>a $X = frac {a - b - 1} {2}$ , $Y = frac {a + b + 1} {2}$ 2N=a*b 意思是 a和b是2N的系数 ，我们知道 X和Y是整数 所以 1. b–a–1=>2的倍数（偶数） 2. b+a+1=>2的倍数（偶数）

这两个条件都必须满足

从1到2我们可以说 其中一个（a，b）应该是奇数，另一个是偶数

所以如果数字 （2N） 只有 奇数因子（不可能，因为它是偶数（2N不是N）） 或 只有偶数因子，我们不能把它表示为任何连续自然数的和

所以现在，我们必须现在 只检查它是否有一个奇怪的因素

1.如果号码 （2N不是N） 做 没有任何奇怪的因素 （仅包含 偶数因子 手段可以是 代表为 $2 ^ k$ )然后 我们不能把它表示为连续数的和

2.如果号码 （2N不是N） 有一个 奇数因子 然后 我们可以把它表示为一个连续数的和

在这之后，我们只需要检查我们是否可以代表 （2N as） $2^k$ ) 还是不行

如果对那么答案是 错还是0

如果不那么答案是 对还是1

以下是上述理念的实施情况：

C++14

                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
                                   
                         long                                     long                                     int                                     canBeSumofConsec(                                     long                                     long                                     int                                     n)                       
                         {                       
                                                 // Updating n with 2n                       
                                                 n = 2 * n;                       
                                                 // (n & (n - 1)) => Checking whether we can write 2n as 2^k                       
                                                 // if yes (can't represent 2n as 2^k) then answer 1                       
                                                 // if no (can represent 2n as 2^k) then answer 0                       
                                                 return                                     ((n & (n - 1)) != 0);                       
                         }                       
                                   
                         int                                     main()                       
                         {                       
                                                 long                                     long                                     int                                     n = 10;                       
                                                 cout<<canBeSumofConsec(n)<<                                     ""                                     ;                       
                         }                       

C

                         #include <stdio.h>                       
                                   
                         long                                     long                                     int                                     canBeSumofConsec(                                     long                                     long                                     int                                     n)                       
                         {                       
                                                 // Updating n with 2n                       
                                                 n = 2 * n;                       
                                                 // (n & (n - 1)) => Checking whether we can write 2n as 2^k                       
                                                 // if yes (can't represent 2n as 2^k) then answer 1                       
                                                 // if no (can represent 2n as 2^k) then answer 0                       
                                                 return                                     ((n & (n - 1)) != 0);                       
                         }                       
                                   
                         int                                     main()                       
                         {                       
                                                 long                                     long                                     int                                     n = 10;                       
                                                 printf                                     (                                     "%lld"                                     , canBeSumofConsec(n));                       
                         }                       

JAVA

                         import                                     java.util.*;                       
                         class                                     GFG{                       
                                   
                                                 static                                     int                                     canBeSumofConsec(                                     int                                     n)                       
                         {                       
                                                 // Updating n with 2n                       
                                                 n =                                     2                                     * n;                       
                                   
                                                 // (n & (n - 1)) => Checking whether we can write 2n as 2^k                       
                                                 // if yes (can't represent 2n as 2^k) then answer 1                       
                                                 // if no (can represent 2n as 2^k) then answer 0                       
                                                 return                                     ((n & (n -                                     1                                     )) !=                                     0                                     )?                                     1                                     :                                     0                                     ;                       
                         }                       
                                   
                         public                                     static                                     void                                     main(String[] args)                       
                         {                       
                                                 int                                     n =                                     10                                     ;                       
                                                 System.out.print(canBeSumofConsec(n)+                                     ""                                     );                       
                         }                       
                         }                       
                                   
                         // This code is contributed by umadevi9616                       

Python3

                         def                                     canBeSumofConsec(n):                       
                                   
                                                 # Updating n with 2n                       
                                                 n                                     =                                     2                                     *                                     n;                       
                                   
                                                 # (n & (n - 1)) => Checking whether we can write 2n as 2^k                       
                                                 # if yes (can't represent 2n as 2^k) then answer 1                       
                                                 # if no (can represent 2n as 2^k) then answer 0                       
                                                 if                                     ((n & (n                                     -                                     1                                     )) !                                     =                                     0                                     ):                       
                                                 return                                     1                                     ;                       
                                                 else                                     :                       
                                                 return                                     0                                     ;                       
                                   
                         if                                     __name__                                     =                                     =                                     '__main__'                                     :                       
                                                 n                                     =                                     10                                     ;                       
                                                 print                                     (canBeSumofConsec(n));                       
                                   
                         # This code is contributed by umadevi9616                       

C#

                         using                                     System;                       
                                   
                         public                                     class                                     GFG {                       
                                   
                                                 static                                     int                                     canBeSumofConsec(                                     int                                     n)                       
                                                 {                       
                                   
                                                 // Updating n with 2n                       
                                                 n = 2 * n;                       
                                   
                                                 // (n & (n - 1)) => Checking whether we can write 2n as 2^k                       
                                                 // if yes (can't represent 2n as 2^k) then answer 1                       
                                                 // if no (can represent 2n as 2^k) then answer 0                       
                                                 return                                     ((n & (n - 1)) != 0) ? 1 : 0;                       
                                                 }                       
                                   
                                                 public                                     static                                     void                                     Main(String[] args) {                       
                                                 int                                     n = 10;                       
                                                 Console.Write(canBeSumofConsec(n) +                                     ""                                     );                       
                                                 }                       
                         }                       
                                   
                         // This code is contributed by umadevi9616                       

Javascript

                         <script>                       
                                   
                                                 function                                     canBeSumofConsec(n) {                       
                                                 // Updating n with 2n                       
                                                 n = 2 * n;                       
                                   
                                                 // (n & (n - 1)) => Checking whether we can write 2n as 2^k                       
                                                 // if yes (can't represent 2n as 2^k) then answer 1                       
                                                 // if no (can represent 2n as 2^k) then answer 0                       
                                                 return                                     ((n & (n - 1)) != 0) ? 1 : 0;                       
                                                 }                       
                                   
                                                 var                                     n = 10;                       
                                                 document.write(canBeSumofConsec(n) +                                     ""                                     );                       
                                   
                         // This code is contributed by umadevi9616                       
                         </script>                       

输出

时间复杂度：O（1）

辅助空间：O（1）

参考： http://www.cut-the-knot.org/arithmetic/UnpropertyOfPowersOf2.shtml 本文由 萨希尔·查布拉 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章