将一块木板切成正方形的最低成本-yiteyi-C++库

给定一块长度为m，宽度为n的木板，我们需要把这块木板分成m*n个正方形，这样一来，破碎的成本就最小了。每一个边缘的削减成本将为董事会给出。简而言之，我们需要选择这样一种削减顺序，以使成本最小化。例如：

null

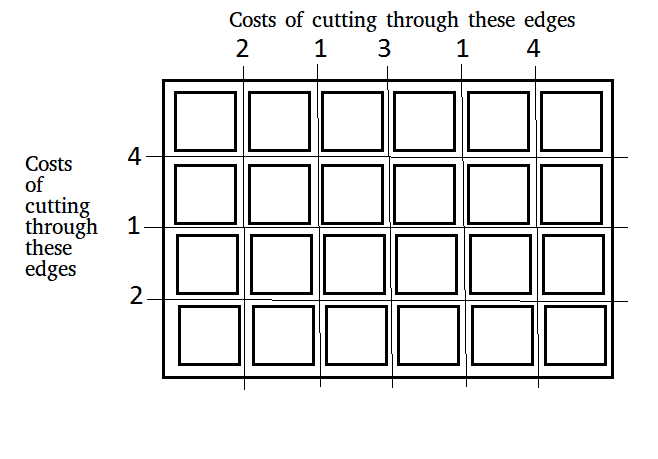
Minimum Cost to cut a board into squares

For above board optimal way to cut into square is:
Total minimum cost in above case is 42. It is 
evaluated using following steps.

Initial Value : Total_cost = 0
Total_cost = Total_cost + edge_cost * total_pieces

Cost 4 Horizontal cut         Cost = 0 + 4*1 = 4
Cost 4 Vertical cut        Cost = 4 + 4*2 = 12
Cost 3 Vertical cut        Cost = 12 + 3*2 = 18
Cost 2 Horizontal cut        Cost = 18 + 2*3 = 24
Cost 2 Vertical cut        Cost = 24 + 2*3 = 30
Cost 1 Horizontal cut        Cost = 30 + 1*4 = 34
Cost 1 Vertical cut        Cost = 34 + 1*4 = 38
Cost 1 Vertical cut        Cost = 38 + 1*4 = 42

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

这个问题可以用贪心方法解决，如果总成本用S表示，那么S=a1w1+a2w2…+akwk，其中wi是某个刃口切割的成本，ai是相应的系数，系数ai由我们在切割过程结束时使用刃口wi竞争的总切割数决定。注意，系数之和总是常数，所以我们想要找到一个可获得的ai分布，使得S最小。这样做 我们尽可能早地在最高成本优势上进行削减 ，这将达到最佳的S。如果我们遇到几个成本相同的边，我们可以先切割其中任何一个。下面是使用上述方法的解决方案，首先我们按相反的顺序对边缘切割成本进行排序，然后我们将它们从高成本循环到低成本构建我们的解决方案。每次我们选择一条边时，对应的数量都会增加1，这将与相应的切边成本相乘。注意下面使用的sort方法，发送greater（）作为sort方法的第三个参数，按非递增顺序对数字进行排序，这是库的预定义函数。

C++

                         //  C++ program to divide a board into m*n squares                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
                                   
                         // method returns minimum cost to break board into                       
                         // m*n squares                       
                         int                                     minimumCostOfBreaking(                                     int                                     X[],                                     int                                     Y[],                                     int                                     m,                                     int                                     n)                       
                         {                       
                                                 int                                     res = 0;                       
                                   
                                                 //  sort the horizontal cost in reverse order                       
                                                 sort(X, X + m, greater<                                     int                                     >());                       
                                   
                                                 //  sort the vertical cost in reverse order                       
                                                 sort(Y, Y + n, greater<                                     int                                     >());                       
                                   
                                                 //  initialize current width as 1                       
                                                 int                                     hzntl = 1, vert = 1;                       
                                   
                                                 //  loop until one or both cost array are processed                       
                                                 int                                     i = 0, j = 0;                       
                                                 while                                     (i < m && j < n)                       
                                                 {                       
                                                 if                                     (X[i] > Y[j])                       
                                                 {                       
                                                 res += X[i] * vert;                       
                                   
                                                 //  increase current horizontal part count by 1                       
                                                 hzntl++;                       
                                                 i++;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 res += Y[j] * hzntl;                       
                                   
                                                 //  increase current vertical part count by 1                       
                                                 vert++;                       
                                                 j++;                       
                                                 }                       
                                                 }                       
                                   
                                                 // loop for horizontal array, if remains                       
                                                 int                                     total = 0;                       
                                                 while                                     (i < m)                       
                                                 total += X[i++];                       
                                                 res += total * vert;                       
                                   
                                                 // loop for vertical array, if remains                       
                                                 total = 0;                       
                                                 while                                     (j < n)                       
                                                 total += Y[j++];                       
                                                 res += total * hzntl;                       
                                   
                                                 return                                     res;                       
                         }                       
                                   
                         //  Driver code to test above methods                       
                         int                                     main()                       
                         {                       
                                                 int                                     m = 6, n = 4;                       
                                                 int                                     X[m-1] = {2, 1, 3, 1, 4};                       
                                                 int                                     Y[n-1] = {4, 1, 2};                       
                                                 cout << minimumCostOfBreaking(X, Y, m-1, n-1);                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to divide a                       
                         // board into m*n squares                       
                         import                                     java.util.Arrays;                       
                         import                                     java.util.Collections;                       
                                   
                         class                                     GFG                       
                         {                       
                                                 // method returns minimum cost to break board into                       
                                                 // m*n squares                       
                                                 static                                     int                                     minimumCostOfBreaking(Integer X[], Integer Y[],                       
                                                 int                                     m,                                     int                                     n)                       
                                                 {                       
                                                 int                                     res =                                     0                                     ;                       
                                   
                                                 // sort the horizontal cost in reverse order                       
                                                 Arrays.sort(X, Collections.reverseOrder());                       
                                   
                                                 // sort the vertical cost in reverse order                       
                                                 Arrays.sort(Y, Collections.reverseOrder());                       
                                   
                                                 // initialize current width as 1                       
                                                 int                                     hzntl =                                     1                                     , vert =                                     1                                     ;                       
                                   
                                                 // loop until one or both                       
                                                 // cost array are processed                       
                                                 int                                     i =                                     0                                     , j =                                     0                                     ;                       
                                                 while                                     (i < m && j < n)                       
                                                 {                       
                                                 if                                     (X[i] > Y[j])                       
                                                 {                       
                                                 res += X[i] * vert;                       
                                   
                                                 // increase current horizontal                       
                                                 // part count by 1                       
                                                 hzntl++;                       
                                                 i++;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 res += Y[j] * hzntl;                       
                                   
                                                 // increase current vertical                       
                                                 // part count by 1                       
                                                 vert++;                       
                                                 j++;                       
                                                 }                       
                                                 }                       
                                   
                                                 // loop for horizontal array,                       
                                                 // if remains                       
                                                 int                                     total =                                     0                                     ;                       
                                                 while                                     (i < m)                       
                                                 total += X[i++];                       
                                                 res += total * vert;                       
                                   
                                                 // loop for vertical array,                       
                                                 // if remains                       
                                                 total =                                     0                                     ;                       
                                                 while                                     (j < n)                       
                                                 total += Y[j++];                       
                                                 res += total * hzntl;                       
                                   
                                                 return                                     res;                       
                                                 }                       
                                   
                                                 // Driver program                       
                                                 public                                     static                                     void                                     main(String arg[])                       
                                                 {                       
                                                 int                                     m =                                     6                                     , n =                                     4                                     ;                       
                                                 Integer X[] = {                                     2                                     ,                                     1                                     ,                                     3                                     ,                                     1                                     ,                                     4                                     };                       
                                                 Integer Y[] = {                                     4                                     ,                                     1                                     ,                                     2                                     };                       
                                                 System.out.print(minimumCostOfBreaking(X, Y, m-                                     1                                     , n-                                     1                                     ));                       
                                                 }                       
                         }                       
                                   
                         // This code is contributed by Anant Agarwal.                       

Python3

                         # Python program to divide a board into m*n squares                       
                                   
                         # Method returns minimum cost to                       
                         # break board into m*n squares                       
                         def                                     minimumCostOfBreaking(X, Y, m, n):                       
                                   
                                                 res                                     =                                     0                       
                                   
                                                 # sort the horizontal cost in reverse order                       
                                                 X.sort(reverse                                     =                                     True                                     )                       
                                   
                                                 # sort the vertical cost in reverse order                       
                                                 Y.sort(reverse                                     =                                     True                                     )                       
                                   
                                                 # initialize current width as 1                       
                                                 hzntl                                     =                                     1                                     ; vert                                     =                                     1                       
                                   
                                                 # loop until one or both                       
                                                 # cost array are processed                       
                                                 i                                     =                                     0                                     ; j                                     =                                     0                       
                                                 while                                     (i < m                                     and                                     j < n):                       
                                   
                                                 if                                     (X[i] > Y[j]):                       
                                   
                                                 res                                     +                                     =                                     X[i]                                     *                                     vert                       
                                   
                                                 # increase current horizontal                       
                                                 # part count by 1                       
                                                 hzntl                                     +                                     =                                     1                       
                                                 i                                     +                                     =                                     1                       
                                   
                                                 else                                     :                       
                                                 res                                     +                                     =                                     Y[j]                                     *                                     hzntl                       
                                   
                                                 # increase current vertical                       
                                                 # part count by 1                       
                                                 vert                                     +                                     =                                     1                       
                                                 j                                     +                                     =                                     1                       
                                   
                                                 # loop for horizontal array, if remains                       
                                                 total                                     =                                     0                       
                                                 while                                     (i < m):                       
                                                 total                                     +                                     =                                     X[i]                       
                                                 i                                     +                                     =                                     1                       
                                                 res                                     +                                     =                                     total                                     *                                     vert                       
                                   
                                                 #loop for vertical array, if remains                       
                                                 total                                     =                                     0                       
                                                 while                                     (j < n):                       
                                                 total                                     +                                     =                                     Y[j]                       
                                                 j                                     +                                     =                                     1                       
                                                 res                                     +                                     =                                     total                                     *                                     hzntl                       
                                   
                                                 return                                     res                       
                                   
                         # Driver program                       
                         m                                     =                                     6                                     ; n                                     =                                     4                       
                         X                                     =                                     [                                     2                                     ,                                     1                                     ,                                     3                                     ,                                     1                                     ,                                     4                                     ]                       
                         Y                                     =                                     [                                     4                                     ,                                     1                                     ,                                     2                                     ]                       
                                   
                         print                                     (minimumCostOfBreaking(X, Y, m                                     -                                     1                                     , n                                     -                                     1                                     ))                       
                                   
                                   
                         # This code is contributed by Anant Agarwal.                       

C#

                         // C# program to divide a                       
                         // board into m*n squares                       
                         using                                     System;                       
                                   
                         class                                     GFG                       
                         {                       
                                                 // method returns minimum cost to break board into                       
                                                 // m*n squares                       
                                                 static                                     int                                     minimumCostOfBreaking(                                     int                                     [] X,                                     int                                     [] Y,                       
                                                 int                                     m,                                     int                                     n)                       
                                                 {                       
                                                 int                                     res = 0;                       
                                   
                                                 // sort the horizontal cost in reverse order                       
                                                 Array.Sort<                                     int                                     >(X,                                     new                                     Comparison<                                     int                                     >(                       
                                                 (i1, i2) => i2.CompareTo(i1)));                       
                                   
                                                 // sort the vertical cost in reverse order                       
                                                 Array.Sort<                                     int                                     >(Y,                                     new                                     Comparison<                                     int                                     >(                       
                                                 (i1, i2) => i2.CompareTo(i1)));                       
                                   
                                                 // initialize current width as 1                       
                                                 int                                     hzntl = 1, vert = 1;                       
                                   
                                                 // loop until one or both                       
                                                 // cost array are processed                       
                                                 int                                     i = 0, j = 0;                       
                                                 while                                     (i < m && j < n)                       
                                                 {                       
                                                 if                                     (X[i] > Y[j])                       
                                                 {                       
                                                 res += X[i] * vert;                       
                                   
                                                 // increase current horizontal                       
                                                 // part count by 1                       
                                                 hzntl++;                       
                                                 i++;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 res += Y[j] * hzntl;                       
                                   
                                                 // increase current vertical                       
                                                 // part count by 1                       
                                                 vert++;                       
                                                 j++;                       
                                                 }                       
                                                 }                       
                                   
                                                 // loop for horizontal array,                       
                                                 // if remains                       
                                                 int                                     total = 0;                       
                                                 while                                     (i < m)                       
                                                 total += X[i++];                       
                                                 res += total * vert;                       
                                   
                                                 // loop for vertical array,                       
                                                 // if remains                       
                                                 total = 0;                       
                                                 while                                     (j < n)                       
                                                 total += Y[j++];                       
                                                 res += total * hzntl;                       
                                   
                                                 return                                     res;                       
                                                 }                       
                                   
                                                 // Driver program                       
                                                 public                                     static                                     void                                     Main(String []arg)                       
                                                 {                       
                                                 int                                     m = 6, n = 4;                       
                                                 int                                     []X = {2, 1, 3, 1, 4};                       
                                                 int                                     []Y = {4, 1, 2};                       
                                                 Console.WriteLine(minimumCostOfBreaking(X, Y, m-1, n-1));                       
                                                 }                       
                         }                       
                                   
                         // This code is contributed by Princi Singh                       

Javascript

                         <script>                       
                                   
                         // JavaScript program to divide a                       
                         // board into m*n squares                       
                                   
                                                 // method returns minimum cost to break board into                       
                                                 // m*n squares                       
                                                 function                                     minimumCostOfBreaking(X, Y,  m, n)                       
                                                 {                       
                                                 let res = 0;                       
                                   
                                                 // sort the horizontal cost in reverse order                       
                                                 X.sort();                       
                                                 X.reverse();                       
                                   
                                                 // sort the vertical cost in reverse order                       
                                                 Y.sort();                       
                                                 Y.reverse();                       
                                   
                                                 // initialize current width as 1                       
                                                 let hzntl = 1, vert = 1;                       
                                   
                                                 // loop until one or both                       
                                                 // cost array are processed                       
                                                 let i = 0, j = 0;                       
                                                 while                                     (i < m && j < n)                       
                                                 {                       
                                                 if                                     (X[i] > Y[j])                       
                                                 {                       
                                                 res += X[i] * vert;                       
                                   
                                                 // increase current horizontal                       
                                                 // part count by 1                       
                                                 hzntl++;                       
                                                 i++;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 res += Y[j] * hzntl;                       
                                   
                                                 // increase current vertical                       
                                                 // part count by 1                       
                                                 vert++;                       
                                                 j++;                       
                                                 }                       
                                                 }                       
                                   
                                                 // loop for horizontal array,                       
                                                 // if remains                       
                                                 let total = 0;                       
                                                 while                                     (i < m)                       
                                                 total += X[i++];                       
                                                 res += total * vert;                       
                                   
                                                 // loop for vertical array,                       
                                                 // if remains                       
                                                 total = 0;                       
                                                 while                                     (j < n)                       
                                                 total += Y[j++];                       
                                                 res += total * hzntl;                       
                                   
                                                 return                                     res;                       
                                                 }                       
                                   
                                   
                         // Driver Code                       
                                   
                                                 let m = 6, n = 4;                       
                                                 let X = [2, 1, 3, 1, 4];                       
                                                 let Y = [4, 1, 2];                       
                                                 document.write(minimumCostOfBreaking(X, Y, m-1, n-1));                       
                                   
                         </script>                       

输出：

本文由 乌特卡什·特里维迪 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章