定积分近似值的梯形法则-yiteyi-C++库

在数值分析领域，梯形法则被用来寻找定积分的近似值。梯形法则的基本思想是假设给定函数图下的区域为梯形，并计算其面积。因此： ${displaystyle int _{a}^{b}f(x),dxapprox (b-a)left[{frac {f(a)+f(b)}{2}} ight]}$ 为了获得更准确的结果，图的域被划分为大小相等的n个段，如下所示：

null

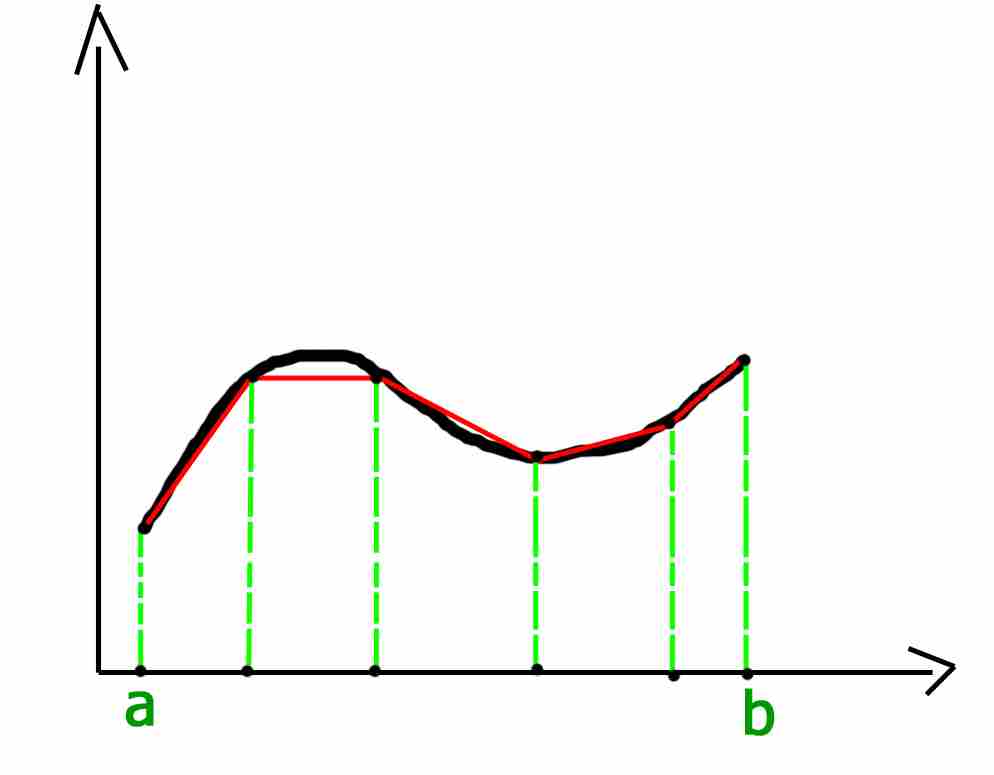
trapezoidalrule2

网格间距或段大小h=（b-a）/n。因此，积分的近似值可通过以下公式得出： $int_{a}^{b}f(x)dx=frac{b-a}{2n}left [ f(a)+2left { sum_{i=1}^{n-1}f(a+ih) ight }+f(b) ight ]$

C++

                         // C++ program to implement Trapezoidal rule                       
                         #include<stdio.h>                       
           
                         // A sample function whose definite integral's                       
                         // approximate value is computed using Trapezoidal                       
                         // rule                       
                         float                                     y(                                     float                                     x)                       
                         {                       
                                                 // Declaring the function f(x) = 1/(1+x*x)                       
                                                 return                                     1/(1+x*x);                       
                         }                       
           
                         // Function to evaluate the value of integral                       
                         float                                     trapezoidal(                                     float                                     a,                                     float                                     b,                                     float                                     n)                       
                         {                       
                                                 // Grid spacing                       
                                                 float                                     h = (b-a)/n;                       
           
                                                 // Computing sum of first and last terms                       
                                                 // in above formula                       
                                                 float                                     s = y(a)+y(b);                       
           
                                                 // Adding middle terms in above formula                       
                                                 for                                     (                                     int                                     i = 1; i < n; i++)                       
                                                 s += 2*y(a+i*h);                       
           
                                                 // h/2 indicates (b-a)/2n. Multiplying h/2                       
                                                 // with s.                       
                                                 return                                     (h/2)*s;                       
                         }                       
           
                         // Driver program to test above function                       
                         int                                     main()                       
                         {                       
                                                 // Range of definite integral                       
                                                 float                                     x0 = 0;                       
                                                 float                                     xn = 1;                       
           
                                                 // Number of grids. Higher value means                       
                                                 // more accuracy                       
                                                 int                                     n = 6;                       
           
                                                 printf                                     (                                     "Value of integral is %6.4f"                                     ,                       
                                                 trapezoidal(x0, xn, n));                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to implement Trapezoidal rule                       
           
                         class                                     GFG                       
                         {                       
                                                 // A sample function whose definite                       
                                                 // integral's approximate value                       
                                                 // is computed using Trapezoidal                       
                                                 // rule                       
                                                 static                                     float                                     y(                                     float                                     x)                       
                                                 {                       
                                                 // Declaring the function                       
                                                 // f(x) = 1/(1+x*x)                       
                                                 return                                     1                                     / (                                     1                                     + x * x);                       
                                                 }                       
                                   
                                                 // Function to evaluate the value of integral                       
                                                 static                                     float                                     trapezoidal(                                     float                                     a,                                     float                                     b,                                     float                                     n)                       
                                                 {                       
                                                 // Grid spacing                       
                                                 float                                     h = (b - a) / n;                       
                                   
                                                 // Computing sum of first and last terms                       
                                                 // in above formula                       
                                                 float                                     s = y(a) + y(b);                       
                                   
                                                 // Adding middle terms in above formula                       
                                                 for                                     (                                     int                                     i =                                     1                                     ; i < n; i++)                       
                                                 s +=                                     2                                     * y( a + i * h);                       
                                   
                                                 // h/2 indicates (b-a)/2n. Multiplying h/2                       
                                                 // with s.                       
                                                 return                                     (h /                                     2                                     ) * s;                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 public                                     static                                     void                                     main (String[] args)                       
                                                 {                       
                                                 // Range of definite integral                       
                                                 float                                     x0 =                                     0                                     ;                       
                                                 float                                     xn =                                     1                                     ;                       
                                   
                                                 // Number of grids. Higher                       
                                                 // value means more accuracy                       
                                                 int                                     n =                                     6                                     ;                       
                                   
                                                 System.out.println(                                     "Value of integral is "                                     +                       
                                                 Math.round(trapezoidal(x0, xn, n)                       
                                                 *                                     10000.0                                     ) /                                     10000.0                                     );                       
                                                 }                       
                         }                       
           
                         // This code is contributed by Anant Agarwal.                       

Python3

                         # Python3 code to implement Trapezoidal rule                       
           
                         # A sample function whose definite                       
                         # integral's approximate value is                       
                         # computed using Trapezoidal rule                       
                         def                                     y( x ):                       
                                   
                                                 # Declaring the function                       
                                                 # f(x) = 1/(1+x*x)                       
                                                 return                                     (                                     1                                     /                                     (                                     1                                     +                                     x                                     *                                     x))                       
                                   
                         # Function to evaluate the value of integral                       
                         def                                     trapezoidal (a, b, n):                       
                                   
                                                 # Grid spacing                       
                                                 h                                     =                                     (b                                     -                                     a)                                     /                                     n                       
                                   
                                                 # Computing sum of first and last terms                       
                                                 # in above formula                       
                                                 s                                     =                                     (y(a)                                     +                                     y(b))                       
           
                                                 # Adding middle terms in above formula                       
                                                 i                                     =                                     1                       
                                                 while                                     i < n:                       
                                                 s                                     +                                     =                                     2                                     *                                     y(a                                     +                                     i                                     *                                     h)                       
                                                 i                                     +                                     =                                     1                       
                                   
                                                 # h/2 indicates (b-a)/2n.                       
                                                 # Multiplying h/2 with s.                       
                                                 return                                     ((h                                     /                                     2                                     )                                     *                                     s)                       
           
                         # Driver code to test above function                       
                         # Range of definite integral                       
                         x0                                     =                                     0                       
                         xn                                     =                                     1                       
           
                         # Number of grids. Higher value means                       
                         # more accuracy                       
                         n                                     =                                     6                       
                         print                                     (                                     "Value of integral is "                                     ,                       
                                                 "%.4f"                                     %                                     trapezoidal(x0, xn, n))                       
           
           
                         # This code is contributed by "Sharad_Bhardwaj".                       

C#

                         // C# program to implement Trapezoidal                       
                         // rule.                       
                         using                                     System;                       
           
                         class                                     GFG {                       
                                   
                                                 // A sample function whose definite                       
                                                 // integral's approximate value                       
                                                 // is computed using Trapezoidal                       
                                                 // rule                       
                                                 static                                     float                                     y(                                     float                                     x)                       
                                                 {                       
                                   
                                                 // Declaring the function                       
                                                 // f(x) = 1/(1+x*x)                       
                                                 return                                     1 / (1 + x * x);                       
                                                 }                       
                                   
                                                 // Function to evaluate the value                       
                                                 // of integral                       
                                                 static                                     float                                     trapezoidal(                                     float                                     a,                       
                                                 float                                     b,                                     float                                     n)                       
                                                 {                       
                                   
                                                 // Grid spacing                       
                                                 float                                     h = (b - a) / n;                       
                                   
                                                 // Computing sum of first and                       
                                                 // last terms in above formula                       
                                                 float                                     s = y(a) + y(b);                       
                                   
                                                 // Adding middle terms in above                       
                                                 // formula                       
                                                 for                                     (                                     int                                     i = 1; i < n; i++)                       
                                                 s += 2 * y( a + i * h);                       
                                   
                                                 // h/2 indicates (b-a)/2n.                       
                                                 // Multiplying h/2 with s.                       
                                                 return                                     (h / 2) * s;                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 public                                     static                                     void                                     Main ()                       
                                                 {                       
                                   
                                                 // Range of definite integral                       
                                                 float                                     x0 = 0;                       
                                                 float                                     xn = 1;                       
                                   
                                                 // Number of grids. Higher                       
                                                 // value means more accuracy                       
                                                 int                                     n = 6;                       
                                   
                                                 Console.Write(                                     "Value of integral is "                       
                                                 + Math.Round(trapezoidal(x0, xn, n)                       
                                                 * 10000.0) / 10000.0);                       
                                                 }                       
                         }                       
           
                         // This code is contributed by nitin mittal.                       

PHP

                         <?php                       
                         // PHP program to implement Trapezoidal rule                       
           
                         // A sample function whose definite                       
                         // integral's approximate value is                       
                         // computed using Trapezoidal rule                       
                         function                                     y(                                     $x                                     )                       
                         {                       
                                   
                                                 // Declaring the function                       
                                                 // f(x) = 1/(1+x*x)                       
                                                 return                                     1 / (1 +                                     $x                                     *                                     $x                                     );                       
                         }                       
           
                         // Function to evaluate the                       
                         // value of integral                       
                         function                                     trapezoidal(                                     $a                                     ,                                     $b                                     ,                                     $n                                     )                       
                         {                       
                                   
                                                 // Grid spacing                       
                                                 $h                                     = (                                     $b                                     -                                     $a                                     ) /                                     $n                                     ;                       
           
                                                 // Computing sum of first                       
                                                 // and last terms                       
                                                 // in above formula                       
                                                 $s                                     = y(                                     $a                                     ) + y(                                     $b                                     );                       
           
                                                 // Adding middle terms                       
                                                 // in above formula                       
                                                 for                                     (                                     $i                                     = 1;                                     $i                                     <                                     $n                                     ;                                     $i                                     ++)                       
                                                 $s                                     += 2 * Y(                                     $a                                     +                                     $i                                     *                                     $h                                     );                       
           
                                                 // h/2 indicates (b-a)/2n.                       
                                                 // Multiplying h/2 with s.                       
                                                 return                                     (                                     $h                                     / 2) *                                     $s                                     ;                       
                         }                       
           
                                                 // Driver Code                       
                                                 // Range of definite integral                       
                                                 $x0                                     = 0;                       
                                                 $xn                                     = 1;                       
           
                                                 // Number of grids.                       
                                                 // Higher value means                       
                                                 // more accuracy                       
                                                 $n                                     = 6;                       
           
                                                 echo                                     (                                     "Value of integral is "                                     );                       
                                                 echo                                     (trapezoidal(                                     $x0                                     ,                                     $xn                                     ,                                     $n                                     ));                       
                                   
                         // This code is contributed by nitin mittal                       
                         ?>                       

Javascript

                         <script>                       
           
                         // Javascript program to implement Trapezoidal rule                       
           
                         // A sample function whose definite                       
                         // integral's approximate value                       
                         // is computed using Trapezoidal                       
                         // rule                       
                         function                                     y(x)                       
                         {                       
                                   
                                                 // Declaring the function                       
                                                 // f(x) = 1/(1+x*x)                       
                                                 return                                     1 / (1 + x * x);                       
                         }                       
                                   
                         // Function to evaluate the value of integral                       
                         function                                     trapezoidal(a, b, n)                       
                         {                       
                                   
                                                 // Grid spacing                       
                                                 let h = (b - a) / n;                       
                                   
                                                 // Computing sum of first and last terms                       
                                                 // in above formula                       
                                                 let s = y(a) + y(b);                       
                                   
                                                 // Adding middle terms in above formula                       
                                                 for                                     (let i = 1; i < n; i++)                       
                                                 s += 2 * y(a + i * h);                       
                                   
                                                 // h/2 indicates (b-a)/2n. Multiplying h/2                       
                                                 // with s.                       
                                                 return                                     (h / 2) * s;                       
                         }                       
           
                         // Driver code                       
           
                         // Range of definite integral                       
                         let x0 = 0;                       
                         let xn = 1;                       
           
                         // Number of grids. Higher                       
                         // value means more accuracy                       
                         let n = 6;                       
           
                         document.write(                                     "Value of integral is "                                     +                       
                                                 Math.round(trapezoidal(x0, xn, n) *                       
                                                 10000.0) / 10000.0);                       
                                   
                         // This code is contributed by code_hunt                       
                                   
                         </script>                       

输出：

Value of integral is 0.7842

参考资料： https://en.wikipedia.org/wiki/Trapezoidal_rule

本文由 严酷的阿加瓦尔 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章