以下是对 二项式系数 .
A. 二项式系数 C(n,k)可以定义为(1+x)^n展开式中x^k的系数。
二项式系数C(n,k)也给出了从n个对象中选择k个对象的方式的数量,而不考虑顺序,更正式地说,是n个元素集的k个元素子集(或k个组合)的数量。
问题 编写一个函数,该函数接受两个参数n和k,并返回二项式系数C(n,k)的值。 例如,对于n=4和k=2,函数应该返回6,并且应该返回 10 对于 n=5 和 k=2 .
1) 最优子结构 C(n,k)的值可以使用以下二项式系数的标准公式递归计算。
C(n, k) = C(n-1, k-1) + C(n-1, k) C(n, 0) = C(n, n) = 1
下面是一个简单的递归实现,它简单地遵循上述递归结构。
C++
// A naive recursive C++ implementation #include <bits/stdc++.h> using namespace std; // Returns value of Binomial Coefficient C(n, k) int binomialCoeff( int n, int k) { // Base Cases if (k > n) return 0; if (k == 0 || k == n) return 1; // Recur return binomialCoeff(n - 1, k - 1) + binomialCoeff(n - 1, k); } /* Driver code*/ int main() { int n = 5, k = 2; cout << "Value of C(" << n << ", " << k << ") is " << binomialCoeff(n, k); return 0; } // This is code is contributed by rathbhupendra |
C
// A Naive Recursive Implementation #include <stdio.h> // Returns value of Binomial Coefficient C(n, k) int binomialCoeff( int n, int k) { // Base Cases if (k > n) return 0; if (k == 0 || k == n) return 1; // Recur return binomialCoeff(n - 1, k - 1) + binomialCoeff(n - 1, k); } /* Driver program to test above function*/ int main() { int n = 5, k = 2; printf ( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k)); return 0; } |
JAVA
// JAVA Code for Dynamic Programming | // Set 9 (Binomial Coefficient) import java.util.*; class GFG { // Returns value of Binomial // Coefficient C(n, k) static int binomialCoeff( int n, int k) { // Base Cases if (k > n) return 0 ; if (k == 0 || k == n) return 1 ; // Recur return binomialCoeff(n - 1 , k - 1 ) + binomialCoeff(n - 1 , k); } /* Driver program to test above function */ public static void main(String[] args) { int n = 5 , k = 2 ; System.out.printf( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k)); } } // This code is contributed by Arnav Kr. Mandal. |
Python3
# A naive recursive Python implementation def binomialCoeff(n, k): if k > n: return 0 if k = = 0 or k = = n: return 1 # Recursive Call return binomialCoeff(n - 1 , k - 1 ) + binomialCoeff(n - 1 , k) # Driver Program to test ht above function n = 5 k = 2 print ( "Value of C(%d,%d) is (%d)" % (n, k, binomialCoeff(n, k))) # This code is contributed by Nikhil Kumar Singh (nickzuck_007) |
C#
// C# Code for Dynamic Programming | // Set 9 (Binomial Coefficient) using System; class GFG { // Returns value of Binomial // Coefficient C(n, k) static int binomialCoeff( int n, int k) { // Base Cases if (k > n) return 0; if (k == 0 || k == n) return 1; // Recur return binomialCoeff(n - 1, k - 1) + binomialCoeff(n - 1, k); } /* Driver program to test above function */ public static void Main() { int n = 5, k = 2; Console.Write( "Value of C(" + n + "," + k + ") is " + binomialCoeff(n, k)); } } // This code is contributed by Sam007. |
PHP
<?php // PHP Code for Dynamic Programming | // Set 9 (Binomial Coefficient) // Returns value of // Binomial Coefficient C(n, k) function binomialCoeff( $n , $k ) { // Base Cases if ( $k > $n ) return 0; if ( $k ==0 || $k == $n ) return 1; // Recur return binomialCoeff( $n - 1, $k - 1) + binomialCoeff( $n - 1, $k ); } // Driver Code $n = 5; $k = 2; echo "Value of C" , "(" , $n , $k , ") is " , binomialCoeff( $n , $k ); // This code is contributed by aj_36 ?> |
Javascript
<script> // javascript Code for Dynamic Programming | // Set 9 (Binomial Coefficient) // Returns value of Binomial // Coefficient C(n, k) function binomialCoeff(n , k) { // Base Cases if (k > n) return 0; if (k == 0 || k == n) return 1; // Recur return binomialCoeff(n - 1, k - 1) + binomialCoeff(n - 1, k); } /* Driver program to test above function */ var n = 5, k = 2; document.write( "Value of C(" +n+ ", " +k+ ") is " +binomialCoeff(n, k)); // This code is contributed by Amit Katiyar </script> |
Value of C(5, 2) is 10
时间复杂性: O(n*max(k,n-k))
辅助空间: O(n*max(k,n-k))
2) 重叠子问题 应该注意的是,上面的函数一次又一次地计算相同的子问题。n=5和k=2见下面的递归树。函数C(3,1)被调用两次。对于n的大值,将有许多常见的子问题。
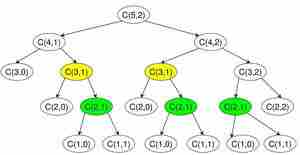
C(5,2)的二项式系数递归树
由于再次调用相同的子问题,此问题具有重叠子问题属性。所以二项式系数问题有两个性质(参见 这 和 这 )一个动态规划问题。像其他典型的 动态规划问题 ,通过以自下而上的方式构造临时二维数组C[]],可以避免对相同子问题的重新计算。以下是基于动态规划的实现。
C++
// A Dynamic Programming based solution that uses // table C[][] to calculate the Binomial Coefficient #include <bits/stdc++.h> using namespace std; // Prototype of a utility function that // returns minimum of two integers int min( int a, int b); // Returns value of Binomial Coefficient C(n, k) int binomialCoeff( int n, int k) { int C[n + 1][k + 1]; int i, j; // Calculate value of Binomial Coefficient // in bottom up manner for (i = 0; i <= n; i++) { for (j = 0; j <= min(i, k); j++) { // Base Cases if (j == 0 || j == i) C[i][j] = 1; // Calculate value using previously // stored values else C[i][j] = C[i - 1][j - 1] + C[i - 1][j]; } } return C[n][k]; } // A utility function to return // minimum of two integers int min( int a, int b) { return (a < b) ? a : b; } // Driver Code int main() { int n = 5, k = 2; cout << "Value of C[" << n << "][" << k << "] is " << binomialCoeff(n, k); } // This code is contributed by Shivi_Aggarwal |
C
// A Dynamic Programming based solution // that uses table C[][] to // calculate the Binomial Coefficient #include <stdio.h> // Prototype of a utility function that // returns minimum of two integers int min( int a, int b); // Returns value of Binomial Coefficient C(n, k) int binomialCoeff( int n, int k) { int C[n + 1][k + 1]; int i, j; // Calculate value of Binomial Coefficient // in bottom up manner for (i = 0; i <= n; i++) { for (j = 0; j <= min(i, k); j++) { // Base Cases if (j == 0 || j == i) C[i][j] = 1; // Calculate value using // previously stored values else C[i][j] = C[i - 1][j - 1] + C[i - 1][j]; } } return C[n][k]; } // A utility function to return // minimum of two integers int min( int a, int b) { return (a < b) ? a : b; } /* Drier program to test above function*/ int main() { int n = 5, k = 2; printf ( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k)); return 0; } |
JAVA
// A Dynamic Programming based // solution that uses table C[][] to // calculate the Binomial Coefficient class BinomialCoefficient { // Returns value of Binomial // Coefficient C(n, k) static int binomialCoeff( int n, int k) { int C[][] = new int [n + 1 ][k + 1 ]; int i, j; // Calculate value of Binomial // Coefficient in bottom up manner for (i = 0 ; i <= n; i++) { for (j = 0 ; j <= min(i, k); j++) { // Base Cases if (j == 0 || j == i) C[i][j] = 1 ; // Calculate value using // previously stored values else C[i][j] = C[i - 1 ][j - 1 ] + C[i - 1 ][j]; } } return C[n][k]; } // A utility function to return // minimum of two integers static int min( int a, int b) { return (a < b) ? a : b; } /* Driver program to test above function*/ public static void main(String args[]) { int n = 5 , k = 2 ; System.out.println( "Value of C(" + n + "," + k + ") is " + binomialCoeff(n, k)); } } /*This code is contributed by Rajat Mishra*/ |
Python3
# A Dynamic Programming based Python # Program that uses table C[][] # to calculate the Binomial Coefficient # Returns value of Binomial Coefficient C(n, k) def binomialCoef(n, k): C = [[ 0 for x in range (k + 1 )] for x in range (n + 1 )] # Calculate value of Binomial # Coefficient in bottom up manner for i in range (n + 1 ): for j in range ( min (i, k) + 1 ): # Base Cases if j = = 0 or j = = i: C[i][j] = 1 # Calculate value using # previously stored values else : C[i][j] = C[i - 1 ][j - 1 ] + C[i - 1 ][j] return C[n][k] # Driver program to test above function n = 5 k = 2 print ( "Value of C[" + str (n) + "][" + str (k) + "] is " + str (binomialCoef(n, k))) # This code is contributed by Bhavya Jain |
C#
// A Dynamic Programming based solution that // uses table C[][] to calculate the Binomial // Coefficient using System; class GFG { // Returns value of Binomial Coefficient // C(n, k) static int binomialCoeff( int n, int k) { int [, ] C = new int [n + 1, k + 1]; int i, j; // Calculate value of Binomial // Coefficient in bottom up manner for (i = 0; i <= n; i++) { for (j = 0; j <= Math.Min(i, k); j++) { // Base Cases if (j == 0 || j == i) C[i, j] = 1; // Calculate value using previously // stored values else C[i, j] = C[i - 1, j - 1] + C[i - 1, j]; } } return C[n, k]; } // A utility function to return minimum // of two integers static int min( int a, int b) { return (a < b) ? a : b; } /* Driver program to test above function*/ public static void Main() { int n = 5, k = 2; Console.WriteLine( "Value of C(" + n + "," + k + ") is " + binomialCoeff(n, k)); } } // This code is contributed by anuj_67. |
PHP
<?php // A Dynamic Programming based // solution that uses table C[][] to // calculate the Binomial Coefficient // Returns value of Binomial // Coefficient C(n, k) function binomialCoeff( $n , $k ) { $C = array ( array ()); $i ; $j ; // Calculate value of Binomial // Coefficient in bottom up manner for ( $i = 0; $i <= $n ; $i ++) { for ( $j = 0; $j <= min( $i , $k ); $j ++) { // Base Cases if ( $j == 0 || $j == $i ) $C [ $i ][ $j ] = 1; // Calculate value using // previously stored values else $C [ $i ][ $j ] = $C [ $i - 1][ $j - 1] + $C [ $i - 1][ $j ]; } } return $C [ $n ][ $k ]; } // Driver Code $n = 5; $k = 2; echo "Value of C(" , $n , " " , $k , ") is" , " " , binomialCoeff( $n , $k ) ; // This code is contributed by anuj_67. ?> |
Javascript
<script> // A Dynamic Programming based // solution that uses table C to // calculate the Binomial Coefficient // Returns value of Binomial // Coefficient C(n, k) function binomialCoeff(n, k) { var C = Array(n + 1).fill(0).map( x => Array(k + 1).fill(0));; var i, j; // Calculate value of Binomial // Coefficient in bottom up manner for (i = 0; i <= n; i++) { for (j = 0; j <= min(i, k); j++) { // Base Cases if (j == 0 || j == i) C[i][j] = 1; // Calculate value using // previously stored values else C[i][j] = C[i - 1][j - 1] + C[i - 1][j]; } } return C[n][k]; } // A utility function to return // minimum of two integers function min(a, b) { return (a < b) ? a : b; } // Driver code var n = 5, k = 2; document.write( "Value of C(" + n + "," + k + ") is " + binomialCoeff(n, k)); // This code is contributed by 29AjayKumar </script> |
Value of C[5][2] is 10
时间复杂性: O(n*k) 辅助空间: O(n*k)
下面是上述代码的空间优化版本。下面的代码只使用O(k)。幸亏 AK 感谢你提出这种方法。
C++
// C++ program for space optimized Dynamic Programming // Solution of Binomial Coefficient #include <bits/stdc++.h> using namespace std; int binomialCoeff( int n, int k) { int C[k + 1]; memset (C, 0, sizeof (C)); C[0] = 1; // nC0 is 1 for ( int i = 1; i <= n; i++) { // Compute next row of pascal triangle using // the previous row for ( int j = min(i, k); j > 0; j--) C[j] = C[j] + C[j - 1]; } return C[k]; } /* Driver code*/ int main() { int n = 5, k = 2; cout << "Value of C(" << n << "," << k << ")" << "is " <<binomialCoeff(n, k); return 0; } // This code is contributed by shivanisinghss2110 |
C
// C++ program for space optimized Dynamic Programming // Solution of Binomial Coefficient #include <stdio.h> int binomialCoeff( int n, int k) { int C[k + 1]; memset (C, 0, sizeof (C)); C[0] = 1; // nC0 is 1 for ( int i = 1; i <= n; i++) { // Compute next row of pascal triangle using // the previous row for ( int j = min(i, k); j > 0; j--) C[j] = C[j] + C[j - 1]; } return C[k]; } /* Driver code*/ int main() { int n = 5, k = 2; printf ( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k)); return 0; } |
JAVA
// JAVA Code for Dynamic Programming | // Set 9 (Binomial Coefficient) import java.util.*; class GFG { static int binomialCoeff( int n, int k) { int C[] = new int [k + 1 ]; // nC0 is 1 C[ 0 ] = 1 ; for ( int i = 1 ; i <= n; i++) { // Compute next row of pascal // triangle using the previous row for ( int j = Math.min(i, k); j > 0 ; j--) C[j] = C[j] + C[j - 1 ]; } return C[k]; } /* Driver code */ public static void main(String[] args) { int n = 5 , k = 2 ; System.out.printf( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k)); } } |
Python3
# Python program for Optimized # Dynamic Programming solution to # Binomial Coefficient. This one # uses the concept of pascal # Triangle and less memory def binomialCoeff(n, k): # Declaring an empty array C = [ 0 for i in range (k + 1 )] C[ 0 ] = 1 # since nC0 is 1 for i in range ( 1 , n + 1 ): # Compute next row of pascal triangle using # the previous row j = min (i, k) while (j > 0 ): C[j] = C[j] + C[j - 1 ] j - = 1 return C[k] # Driver Code n = 5 k = 2 print ( "Value of C(%d,%d) is %d" % (n, k, binomialCoeff(n, k))) # This code is contribtued by Nikhil Kumar Singh(nickzuck_007) |
C#
// C# Code for Dynamic Programming | // Set 9 (Binomial Coefficient) using System; class GFG { static int binomialCoeff( int n, int k) { int [] C = new int [k + 1]; // nC0 is 1 C[0] = 1; for ( int i = 1; i <= n; i++) { // Compute next row of pascal // triangle using the previous // row for ( int j = Math.Min(i, k); j > 0; j--) C[j] = C[j] + C[j - 1]; } return C[k]; } /* Driver Code */ public static void Main() { int n = 5, k = 2; Console.WriteLine( "Value of C(" + n + " " + k + ") is " + binomialCoeff(n, k)); } } // This code is contributed by anuj_67. |
PHP
<?php // PHP program for space optimized // Dynamic Programming Solution of // Binomial Coefficient function binomialCoeff( $n , $k ) { $C = array_fill (0, $k + 1, 0); $C [0] = 1; // nC0 is 1 for ( $i = 1; $i <= $n ; $i ++) { // Compute next row of pascal // triangle using the previous row for ( $j = min( $i , $k ); $j > 0; $j --) $C [ $j ] = $C [ $j ] + $C [ $j - 1]; } return $C [ $k ]; } // Driver Code $n = 5; $k = 2; echo "Value of C[$n, $k] is " . binomialCoeff( $n , $k ); // This code is contributed by mits. ?> |
Javascript
<script> // Javascript program for space optimized // Dynamic Programming // Solution of Binomial Coefficient function binomialCoeff(n, k) { let C = new Array(k + 1); C.fill(0); // nC0 is 1 C[0] = 1; for (let i = 1; i <= n; i++) { // Compute next row of pascal // triangle using the previous // row for (let j = Math.min(i, k); j > 0; j--) C[j] = C[j] + C[j - 1]; } return C[k]; } // Driver code let n = 5, k = 2; document.write( "Value of C(" + n + " " + k + ") is " + binomialCoeff(n, k)); // This code is contributed by divyesh072019 </script> |
Value of C(5, 2) is 10
时间复杂性: O(n*k) 辅助空间: O(k)
说明: 1====>>n=0,C(0,0)=1 1-1=n=1,C(1,0)=1,C(1,1)=1 1-2-1=n=2,C(2,0)=1,C(2,1)=2,C(2,2)=1 1-3-3-1==>>n=3,C(3,0)=1,C(3,1)=3,C(3,2)=3,C(3,3)=1 1-4-6-4-1=>>n=4,C(4,0)=1,C(4,1)=4,C(4,2)=6,C(4,3)=4,C(4,4)=1 在这里,i上的每个循环,用第(i-1)行,建立帕斯卡三角形的第i行 在任何时候,数组C的每个元素都会有一些值(零或更多),在下一次迭代中,这些元素的值来自上一次迭代。 在声明中, C[j]=C[j]+C[j-1] 右边代表来自上一次迭代的值(帕斯卡三角形的一行取决于上一行)。左侧代表当前迭代的值,该值将通过该语句获得。
Let's say we want to calculate C(4, 3), i.e. n=4, k=3:All elements of array C of size 4 (k+1) areinitialized to ZERO.i.e. C[0] = C[1] = C[2] = C[3] = C[4] = 0;Then C[0] is set to 1For i = 1:C[1] = C[1] + C[0] = 0 + 1 = 1 ==>> C(1,1) = 1For i = 2:C[2] = C[2] + C[1] = 0 + 1 = 1 ==>> C(2,2) = 1C[1] = C[1] + C[0] = 1 + 1 = 2 ==>> C(2,1) = 2For i=3:C[3] = C[3] + C[2] = 0 + 1 = 1 ==>> C(3,3) = 1C[2] = C[2] + C[1] = 1 + 2 = 3 ==>> C(3,2) = 3C[1] = C[1] + C[0] = 2 + 1 = 3 ==>> C(3,1) = 3For i=4:C[4] = C[4] + C[3] = 0 + 1 = 1 ==>> C(4,4) = 1C[3] = C[3] + C[2] = 1 + 3 = 4 ==>> C(4,3) = 4C[2] = C[2] + C[1] = 3 + 3 = 6 ==>> C(4,2) = 6C[1] = C[1] + C[0] = 3 + 1 = 4 ==>> C(4,1) = 4C(4,3) = 4 is would be the answer in our example.
记忆化方法: 其想法是创建一个查找表,并遵循递归自上而下的方法。在计算任何值之前,我们检查它是否已经在查找表中。如果是,则返回值。否则,我们计算该值并将其存储在查找表中。以下是自上而下的动态规划方法,用于寻找二项式系数的值。
C++
// A Dynamic Programming based // solution that uses // table dp[][] to calculate // the Binomial Coefficient // A naive recursive approach // with table C++ implementation #include <bits/stdc++.h> using namespace std; // Returns value of Binomial Coefficient C(n, k) int binomialCoeffUtil( int n, int k, int ** dp) { // If value in lookup table then return if (dp[n][k] != -1) // return dp[n][k]; // store value in a table before return if (k == 0) { dp[n][k] = 1; return dp[n][k]; } // store value in table before return if (k == n) { dp[n][k] = 1; return dp[n][k]; } // save value in lookup table before return dp[n][k] = binomialCoeffUtil(n - 1, k - 1, dp) + binomialCoeffUtil(n - 1, k, dp); return dp[n][k]; } int binomialCoeff( int n, int k) { int ** dp; // make a temporary lookup table dp = new int *[n + 1]; // loop to create table dynamically for ( int i = 0; i < (n + 1); i++) { dp[i] = new int [k + 1]; } // nested loop to initialise the table with -1 for ( int i = 0; i < (n + 1); i++) { for ( int j = 0; j < (k + 1); j++) { dp[i][j] = -1; } } return binomialCoeffUtil(n, k, dp); } /* Driver code*/ int main() { int n = 5, k = 2; cout << "Value of C(" << n << ", " << k << ") is " << binomialCoeff(n, k) << endl; return 0; } // This is code is contributed by MOHAMMAD MUDASSIR |
JAVA
// A Dynamic Programming based // solution that uses // table dp[][] to calculate // the Binomial Coefficient // A naive recursive approach // with table Java implementation import java.util.*; class GFG{ // Returns value of Binomial // Coefficient C(n, k) static int binomialCoeffUtil( int n, int k, Vector<Integer> []dp) { // If value in lookup table // then return if (dp[n].get(k) != - 1 ) return dp[n].get(k); // store value in a table // before return if (k == 0 ) { dp[n].add(k, 1 ); return dp[n].get(k); } // store value in table // before return if (k == n) { dp[n].add(k, 1 ); return dp[n].get(k); } // save value in lookup table // before return dp[n].add(k, binomialCoeffUtil(n - 1 , k - 1 , dp) + binomialCoeffUtil(n - 1 , k, dp)); return dp[n].get(k); } static int binomialCoeff( int n, int k) { // Make a temporary lookup table Vector<Integer> []dp = new Vector[n+ 1 ]; // Loop to create table dynamically for ( int i = 0 ; i < (n + 1 ); i++) { dp[i] = new Vector<Integer>(); for ( int j = 0 ; j <= k; j++) dp[i].add(- 1 ); } return binomialCoeffUtil(n, k, dp); } // Driver code public static void main(String[] args) { int n = 5 , k = 2 ; System.out.print( "Value of C(" + n + ", " + k + ") is " + binomialCoeff(n, k) + "" ); } } // This code is contributed by Rajput-Ji |
Python3
# A Dynamic Programming based solution # that uses table dp[][] to calculate # the Binomial Coefficient. A naive # recursive approach with table # Python3 implementation # Returns value of Binomial # Coefficient C(n, k) def binomialCoeffUtil(n, k, dp): # If value in lookup table then return if dp[n][k] ! = - 1 : return dp[n][k] # Store value in a table before return if k = = 0 : dp[n][k] = 1 return dp[n][k] # Store value in table before return if k = = n: dp[n][k] = 1 return dp[n][k] # Save value in lookup table before return dp[n][k] = (binomialCoeffUtil(n - 1 , k - 1 , dp) + binomialCoeffUtil(n - 1 , k, dp)) return dp[n][k] def binomialCoeff(n, k): # Make a temporary lookup table dp = [ [ - 1 for y in range (k + 1 ) ] for x in range (n + 1 ) ] return binomialCoeffUtil(n, k, dp) # Driver code n = 5 k = 2 print ( "Value of C(" + str (n) + ", " + str (k) + ") is" , binomialCoeff(n, k)) # This is code is contributed by Prateek Gupta |
C#
// C# program for the // above approach // A Dynamic Programming based // solution that uses // table [,]dp to calculate // the Binomial Coefficient // A naive recursive approach // with table C# implementation using System; using System.Collections.Generic; class GFG{ // Returns value of Binomial // Coefficient C(n, k) static int binomialCoeffUtil( int n, int k, List< int > []dp) { // If value in lookup table // then return if (dp[n][k] != -1) return dp[n][k]; // store value in a table // before return if (k == 0) { dp[n][k] = 1; return dp[n][k]; } // store value in table // before return if (k == n) { dp[n][k] = 1; return dp[n][k]; } // save value in lookup table // before return dp[n][k] = binomialCoeffUtil(n - 1, k - 1, dp) + binomialCoeffUtil(n - 1, k, dp); return dp[n][k]; } static int binomialCoeff( int n, int k) { // Make a temporary lookup table List< int > []dp = new List< int >[n + 1]; // Loop to create table dynamically for ( int i = 0; i < (n + 1); i++) { dp[i] = new List< int >(); for ( int j = 0; j <= k; j++) dp[i].Add(-1); } return binomialCoeffUtil(n, k, dp); } // Driver code public static void Main(String[] args) { int n = 5, k = 2; Console.Write( "Value of C(" + n + ", " + k + ") is " + binomialCoeff(n, k) + "" ); } } // This code is contributed by 29AjayKumar |
Javascript
<script> // A Dynamic Programming based solution that // uses table dp[][] to calculate the // Binomial Coefficient. A naive recursive // approach with table Javascript implementation // Returns value of Binomial // Coefficient C(n, k) function binomialCoeffUtil(n, k, dp) { // If value in lookup table // then return if (dp[n][k] != -1) return dp[n][k]; // Store value in a table // before return if (k == 0) { dp[n][k] = 1; return dp[n][k]; } // Store value in table // before return if (k == n) { dp[n][k] = 1; return dp[n][k]; } // Save value in lookup table // before return dp[n][k] = binomialCoeffUtil(n - 1, k - 1, dp) + binomialCoeffUtil(n - 1, k, dp); return dp[n][k]; } function binomialCoeff(n, k) { // Make a temporary lookup table let dp = new Array(n + 1); // Loop to create table dynamically for (let i = 0; i < (n + 1); i++) { dp[i] = []; for (let j = 0; j <= k; j++) dp[i].push(-1); } return binomialCoeffUtil(n, k, dp); } // Driver code let n = 5, k = 2; document.write( "Value of C(" + n + ", " + k + ") is " + binomialCoeff(n, k) + "" ); // This code is contributed by avanitrachhadiya2155 </script> |
时间复杂性: O(最大值(n,n-k))
辅助空间: O(n*k)
Value of C(5, 2) is 10
取消分子和分母之间的因子:
nCr=(n-r+1)*(n-r+2)**n/(r!)
创建一个从n-r+1到n的数字数组arr,其大小为r。由于nCr始终是一个整数,分母中的所有数字都应与分子(由arr表示)的乘积相消。
对于i=1到i=r,
搜索arr,如果arr[j]和我的gcd>1,则除以gcd,当我变为1时,停止搜索
现在,答案就是arr的乘积,它的值mod 10^9+7可以通过一次传递找到,公式使用(a*b)%mod=(a%mod*b%mod)%mod
C++
// C++ program to find gcd of // two numbers in O(log(min(a,b))) #include <bits/stdc++.h> using namespace std; int gcd( int a, int b) { if (b == 0) return a; return gcd(b, a % b); } int nCr( int n, int r) { // base case if (r > n) return 0; // C(n,r) = C(n,n-r) if (r > n - r) r = n - r; int mod = 1000000007; // array of elements from n-r+1 to n int arr[r]; for ( int i = n - r + 1; i <= n; i++) { arr[i + r - n - 1] = i; } long int ans = 1; // for numbers from 1 to r find arr[j], // such that gcd(i,arr[j])>1 for ( int k = 1; k < r + 1; k++) { int j = 0, i = k; while (j < r) { int x = gcd(i, arr[j]); if (x > 1) { // if gcd>1, divide both by gcd arr[j] /= x; i /= x; } // if i becomes 1, no need to search arr if (i == 1) break ; j += 1; } } // single pass to multiply the numerator for ( int i : arr) ans = (ans * i) % mod; return ( int )ans; } int main() { int n = 5, r = 2; cout << "Value of C(" << n << ", " << r << ") is " << nCr(n, r) << "" ; return 0; } // This code is contributed by rajsanghavi9. |
JAVA
import java.util.*; class GFG { static int gcd( int a, int b) // function to find gcd of two numbers in O(log(min(a,b))) { if (b== 0 ) return a; return gcd(b,a%b); } static int nCr( int n, int r) { if (r>n) // base case return 0 ; if (r>n-r) // C(n,r) = C(n,n-r) better time complexity for lesser r value r = n-r; int mod = 1000000007 ; int [] arr = new int [r]; // array of elements from n-r+1 to n for ( int i=n-r+ 1 ; i<=n; i++) { arr[i+r-n- 1 ] = i; } long ans = 1 ; for ( int k= 1 ;k<r+ 1 ;k++) // for numbers from 1 to r find arr[j] such that gcd(i,arr[j])>1 { int j= 0 , i=k; while (j<arr.length) { int x = gcd(i,arr[j]); if (x> 1 ) { arr[j] /= x; // if gcd>1, divide both by gcd i /= x; } if (i== 1 ) break ; // if i becomes 1, no need to search arr j += 1 ; } } for ( int i : arr) // single pass to multiply the numerator ans = (ans*i)%mod; return ( int )ans; } // Driver code public static void main(String[] args) { int n = 5 , r = 2 ; System.out.print( "Value of C(" + n+ ", " + r+ ") is " +nCr(n, r) + "" ); } } // This code is contributed by Gautam Wadhwani |
Python3
import math class GFG: def nCr( self , n, r): def gcd(a,b): # function to find gcd of two numbers in O(log(min(a,b))) if b = = 0 : # base case return a return gcd(b,a % b) if r>n: return 0 if r>n - r: # C(n,r) = C(n,n-r) better time complexity for lesser r value r = n - r mod = 10 * * 9 + 7 arr = list ( range (n - r + 1 ,n + 1 )) # array of elements from n-r+1 to n ans = 1 for i in range ( 1 ,r + 1 ): # for numbers from 1 to r find arr[j] such that gcd(i,arr[j])>1 j = 0 while j< len (arr): x = gcd(i,arr[j]) if x> 1 : arr[j] / / = x # if gcd>1, divide both by gcd i / / = x if arr[j] = = 1 : # if element becomes 1, its of no use anymore so delete from arr del arr[j] j - = 1 if i = = 1 : break # if i becomes 1, no need to search arr j + = 1 for i in arr: # single pass to multiply the numerator ans = (ans * i) % mod return ans # Driver code n = 5 k = 2 ob = GFG() print ( "Value of C(" + str (n) + ", " + str (k) + ") is" , ob.nCr(n, k)) # This is code is contributed by Gautam Wadhwani |
C#
using System; class GFG{ // Function to find gcd of two numbers // in O(log(min(a,b))) static int gcd( int a, int b) { if (b == 0) return a; return gcd(b, a % b); } static int nCr( int n, int r) { // Base case if (r > n) return 0; // C(n,r) = C(n,n-r) better time // complexity for lesser r value if (r > n - r) r = n - r; int mod = 1000000007; // Array of elements from n-r+1 to n int [] arr = new int [r]; for ( int i = n - r + 1; i <= n; i++) { arr[i + r - n - 1] = i; } long ans = 1; // For numbers from 1 to r find arr[j] // such that gcd(i,arr[j])>1 for ( int k = 1; k < r + 1; k++) { int j = 0, i = k; while (j < arr.Length) { int x = gcd(i,arr[j]); if (x > 1) { // If gcd>1, divide both by gcd arr[j] /= x; i /= x; } if (i == 1) // If i becomes 1, no need // to search arr break ; j += 1; } } // Single pass to multiply the numerator foreach ( int i in arr) ans = (ans * i) % mod; return ( int )ans; } // Driver code static public void Main() { int n = 5, r = 2; Console.WriteLine( "Value of C(" + n + ", " + r + ") is " + nCr(n, r) + "" ); } } // This code is contributed by rag2127 |
Javascript
<script> // Javascript program to find gcd of // two numbers in O(log(min(a,b))) function gcd(a, b) { if (b == 0) return a; return gcd(b, a % b); } function nCr(n, r) { // Base case if (r > n) return 0; // C(n,r) = C(n,n-r) better time // complexity for lesser r value if (r > n - r) r = n - r; mod = 1000000007; // Array of elements from n-r+1 to n var arr = new Array(r); for ( var i = n - r + 1; i <= n; i++) { arr[i + r - n - 1] = i; } var ans = 1; // For numbers from 1 to r find arr[j] // such that gcd(i,arr[j])>1 for ( var k = 1; k < r + 1 ; k++) { var j = 0, i = k; while (j < arr.length) { var x = gcd(i, arr[j]); if (x > 1) { // If gcd>1, divide both by gcd arr[j] /= x; i /= x; } // If i becomes 1, no need to search arr if (i == 1) break ; j += 1; } } // Single pass to multiply the numerator arr.forEach( function (i) { ans = (ans * i) % mod; }); return ans; } // Driver code var n = 5, r = 2; document.write( "Value of C(" + n + ", " + r + ") is " + nCr(n, r) + "" ); // This code is contributed by shivanisinghss2110 </script> |
Value of C(5, 2) is 10
时间复杂性: O((最小(r,n-r)^2)*对数(n)), 当n>>r或n>>(n-r)时有用
辅助空间: O(最小(r,n-r))
看看这个 对数时间的GCD
使用Eratosthenes筛对从1到n的每个数字进行素因式分解:
1.创建一个大小为n+1的数组SPF,每个数的最小素数因子为1到n
Set SPF[i] = i for all i = 1 to i = n
2.使用Eratosthenes筛:
for i = 2 to i = n: if i is prime, for all multiples j of i, j<=n: if SPF[j] equals j, set SPF[j] = i
3.一旦我们知道了从1到n的每个数的SPF,我们就可以在O(log(n))时间内使用SPF的递归除法找到从1到n的任何数的素因式分解,直到该数变为1
Now, nCr = (n-r+1)*(r+2)* ... *(n) / (r)!
4.创建一个字典(或hashmap)来存储nCr实际值的素数分解中每个素数的频率。
5.所以,只需计算nCr中每个素数的频率,并将它们乘以其频率的幂。
6.对于分子,通过i=n-r+1迭代到i=n,对于i的所有素数因子,将其频率存储在字典中。
( prime_pow[prime_factor] += freq_in_i )
7.对于分母,迭代i=1到i=r,现在减去频率,而不是相加。
8.现在,遍历字典,将(prime^prime_pow[prime])%(10^9+7)的答案相乘
ans = (ans * pow(prime, prime_pow[prime], mod) ) % mod
C++
#include <bits/stdc++.h> using namespace std; // pow(base,exp,mod) is used to find // (base^exp)%mod fast -> O(log(exp)) long int pow ( long int b, long int exp , long int mod) { long int ret = 1; while ( exp > 0) { if (( exp & 1) > 0) ret = (ret * b) % mod; b = (b * b) % mod; exp >>= 1; } return ret; } int nCr( int n, int r) { // base case if (r > n) return 0; // C(n,r) = C(n,n-r) Complexity for // this code is lesser for lower n-r if (n - r > r) r = n - r; // list to smallest prime factor // of each number from 1 to n int SPF[n + 1]; // set smallest prime factor of each // number as itself for ( int i = 1; i <= n; i++) SPF[i] = i; // set smallest prime factor of all // even numbers as 2 for ( int i = 4; i <= n; i += 2) SPF[i] = 2; for ( int i = 3; i * i < n + 1; i += 2) { // Check if i is prime if (SPF[i] == i) { // All multiples of i are // composite (and divisible by // i) so add i to their prime // factorization getpow(j,i) // times for ( int j = i * i; j < n + 1; j += i) if (SPF[j] == j) { SPF[j] = i; } } } // Hash Map to store power of // each prime in C(n,r) map< int , int > prime_pow; // For numerator count frequency of each prime factor for ( int i = r + 1; i < n + 1; i++) { int t = i; // Recursive division to find // prime factorization of i while (t > 1) { if (!prime_pow[SPF[t]]) { prime_pow[SPF[t]] = 1; } else prime_pow[SPF[t]]++; // prime_pow.put(SPF[t], // prime_pow.getOrDefault(SPF[t], 0) // + 1); t /= SPF[t]; } } // For denominator subtract the power of // each prime factor for ( int i = 1; i < n - r + 1; i++) { int t = i; // Recursive division to find // prime factorization of i while (t > 1) { prime_pow[SPF[t]]--; // prime_pow.put(SPF[t], // prime_pow.get(SPF[t]) - 1); t /= SPF[t]; } } // long because mod is large and a%mod // * b%mod can overflow int long int ans = 1, mod = 1000000007; // use (a*b)%mod = (a%mod * b%mod)%mod for ( auto it : prime_pow) // pow(base,exp,mod) is used to // find (base^exp)%mod fast ans = (ans * pow (it.first, prime_pow[it.first], mod)) % mod; return ( int )ans; } int main() { int n = 5, r = 2; cout << "Value of C(" << n << ", " << r << ") is " << nCr(n, r) << "" ; return 0; } // This code is contributed by rajsanghavi9. |
JAVA
import java.util.*; class GFG { // pow(base,exp,mod) is used to find // (base^exp)%mod fast -> O(log(exp)) static long pow( long b, long exp, long mod) { long ret = 1 ; while (exp > 0 ) { if ((exp & 1 ) > 0 ) ret = (ret * b) % mod; b = (b * b) % mod; exp >>= 1 ; } return ret; } static int nCr( int n, int r) { if (r > n) // base case return 0 ; // C(n,r) = C(n,n-r) Complexity for // this code is lesser for lower n-r if (n - r > r) r = n - r; // list to smallest prime factor // of each number from 1 to n int [] SPF = new int [n + 1 ]; // set smallest prime factor of each // number as itself for ( int i = 1 ; i <= n; i++) SPF[i] = i; // set smallest prime factor of all // even numbers as 2 for ( int i = 4 ; i <= n; i += 2 ) SPF[i] = 2 ; for ( int i = 3 ; i * i < n + 1 ; i += 2 ) { // Check if i is prime if (SPF[i] == i) { // All multiples of i are // composite (and divisible by // i) so add i to their prime // factorization getpow(j,i) // times for ( int j = i * i; j < n + 1 ; j += i) if (SPF[j] == j) { SPF[j] = i; } } } // Hash Map to store power of // each prime in C(n,r) Map<Integer, Integer> prime_pow = new HashMap<>(); // For numerator count frequency of each prime factor for ( int i = r + 1 ; i < n + 1 ; i++) { int t = i; // Recursive division to find // prime factorization of i while (t > 1 ) { prime_pow.put(SPF[t], prime_pow.getOrDefault(SPF[t], 0 ) + 1 ); t /= SPF[t]; } } // For denominator subtract the power of // each prime factor for ( int i = 1 ; i < n - r + 1 ; i++) { int t = i; // Recursive division to find // prime factorization of i while (t > 1 ) { prime_pow.put(SPF[t], prime_pow.get(SPF[t]) - 1 ); t /= SPF[t]; } } // long because mod is large and a%mod // * b%mod can overflow int long ans = 1 , mod = 1000000007 ; // use (a*b)%mod = (a%mod * b%mod)%mod for ( int i : prime_pow.keySet()) // pow(base,exp,mod) is used to // find (base^exp)%mod fast ans = (ans * pow(i, prime_pow.get(i), mod)) % mod; return ( int )ans; } // Driver code public static void main(String[] args) { int n = 5 , r = 2 ; System.out.print( "Value of C(" + n + ", " + r + ") is " + nCr(n, r) + "" ); } } // This code is contributed by Gautam Wadhwani |
Python3
# Python code for the above approach import math class GFG: def nCr( self , n, r): # Base case if r > n: return 0 # C(n,r) = C(n,n-r) Complexity for this # code is lesser for lower n-r if n - r > r: r = n - r # List to store smallest prime factor # of every number from 1 to n SPF = [i for i in range (n + 1 )] for i in range ( 4 , n + 1 , 2 ): # set smallest prime factor of # all even numbers as 2 SPF[i] = 2 for i in range ( 3 , n + 1 , 2 ): if i * i > n: break # Check if i is prime if SPF[i] = = i: # All multiples of i are composite # (and divisible by i) so add i to # their prime factorization getpow(j,i) times for j in range (i * i, n + 1 , i): if SPF[j] = = j: # set smallest prime factor # of j to i only if it is # not previously set SPF[j] = i # dictionary to store power of each prime in C(n,r) prime_pow = {} # For numerator count frequency # of each prime factor for i in range (r + 1 , n + 1 ): t = i # Recursive division to # find prime factorization of i while t > 1 : if not SPF[t] in prime_pow: prime_pow[SPF[t]] = 1 else : prime_pow[SPF[t]] + = 1 t / / = SPF[t] # For denominator subtract the # power of each prime factor for i in range ( 1 , n - r + 1 ): t = i # Recursive division to # find prime factorization of i while t > 1 : prime_pow[SPF[t]] - = 1 t / / = SPF[t] ans = 1 mod = 10 * * 9 + 7 # Use (a*b)%mod = (a%mod * b%mod)%mod for i in prime_pow: # pow(base,exp,mod) is used to # find (base^exp)%mod fast ans = (ans * pow (i, prime_pow[i], mod)) % mod return ans # Driver code n = 5 k = 2 ob = GFG() print ( "Value of C(" + str (n) + ", " + str (k) + ") is" , ob.nCr(n, k)) # This is code is contributed by Gautam Wadhwani |
C#
using System; using System.Collections.Generic; public class GFG { // pow(base,exp,mod) is used to find // (base^exp)%mod fast -> O(log(exp)) static long pow( long b, long exp, long mod) { long ret = 1; while (exp > 0) { if ((exp & 1) > 0) ret = (ret * b) % mod; b = (b * b) % mod; exp >>= 1; } return ret; } static int nCr( int n, int r) { if (r > n) // base case return 0; // C(n,r) = C(n,n-r) Complexity for // this code is lesser for lower n-r if (n - r > r) r = n - r; // list to smallest prime factor // of each number from 1 to n int [] SPF = new int [n + 1]; // set smallest prime factor of each // number as itself for ( int i = 1; i <= n; i++) SPF[i] = i; // set smallest prime factor of all // even numbers as 2 for ( int i = 4; i <= n; i += 2) SPF[i] = 2; for ( int i = 3; i * i < n + 1; i += 2) { // Check if i is prime if (SPF[i] == i) { // All multiples of i are // composite (and divisible by // i) so add i to their prime // factorization getpow(j,i) // times for ( int j = i * i; j < n + 1; j += i) if (SPF[j] == j) { SPF[j] = i; } } } // Hash Map to store power of // each prime in C(n,r) Dictionary< int , int > prime_pow = new Dictionary< int , int >(); // For numerator count frequency of each prime // factor for ( int i = r + 1; i < n + 1; i++) { int t = i; // Recursive division to find // prime factorization of i while (t > 1) { if (prime_pow.ContainsKey(SPF[t])) { prime_pow[SPF[t]] = prime_pow[SPF[t]] + 1; } else { prime_pow.Add(SPF[t], 1); } t /= SPF[t]; } } // For denominator subtract the power of // each prime factor for ( int i = 1; i < n - r + 1; i++) { int t = i; // Recursive division to find // prime factorization of i while (t > 1) { if (prime_pow.ContainsKey(SPF[t])) { prime_pow[SPF[t]] = prime_pow[SPF[t]] - 1; } t /= SPF[t]; } } // long because mod is large and a%mod // * b%mod can overflow int long ans = 1, mod = 1000000007; // use (a*b)%mod = (a%mod * b%mod)%mod foreach ( int i in prime_pow.Keys) // pow(base,exp,mod) is used to // find (base^exp)%mod fast ans = (ans * pow(i, prime_pow[i], mod)) % mod; return ( int )ans; } // Driver code public static void Main(String[] args) { int n = 5, r = 2; Console.Write( "Value of C(" + n + ", " + r + ") is " + nCr(n, r) + "" ); } } // This code contributed by gauravrajput1 |
Javascript
<script> // Javascript program to find gcd of // two numbers in O(log(min(a,b))) function gcd(a, b) { if (b == 0) return a; return gcd(b, a % b); } function nCr(n, r) { // base case if (r > n) return 0; // C(n,r) = C(n,n-r) if (r > n - r) r = n - r; var mod = 1000000007; // array of elements from n-r+1 to n var arr = new Array(r); for ( var i = n - r + 1; i <= n; i++) { arr[i + r - n - 1] = i; } var ans = 1; // for numbers from 1 to r find arr[j], // such that gcd(i,arr[j])>1 for ( var k = 1; k < r + 1; k++) { var j = 0; var i = k; do { var x = gcd(i, arr[j]); if (x > 1) { // if gcd>1, divide both by gcd arr[j] /= x; i /= x; } // if i becomes 1, no need to search arr if (i == 1) break ; j += 1; } while (j < r); } // single pass to multiply the numerator arr.forEach( function (i, index) { ans = (ans * i) % mod; }); return ans; } var n = 5; var r = 2; document.write( "Value of C(" + n + ", " + r + ") is " + nCr(n, r) + "<br>" ); // This code is contributed by shivani. </script> |
Value of C(5, 2) is 10
时间复杂性: O(n*log(n)), 当r->n/2时非常有用
辅助空间: O(n)
看看这个 O(log(n))中的素因子分解
另一种方法:(模逆技术)
1.nCr的一般公式为(n*(n-1)*(n-2)*……*(n-r+1))/(r!)。我们可以直接用这个公式来计算nCr。但这将超出范围。我们需要找到nCr mod m,这样它就不会溢出。我们可以很容易地用模运算公式来做。
for the n*(n-1)*(n-2)* ... *(n-r+1) part we can use the formula,(a*b) mod m = ((a % m) * (b % m)) % m
2.还有1/r!第二部分,我们需要找到从1到r的每个数的模逆。然后使用上面的公式,用1到r的模逆。我们可以用这个公式在O(r)时间内找到模逆,
inv[1] = 1inv[i] = − ⌊m/i⌋ * inv[m mod i] mod mTo use this formula, m has to be a prime.
在实际问题中,我们需要用模100000007表示答案,这是一个素数。
所以,这项技术会奏效。
C++
// C++ program for the above approach #include<bits/stdc++.h> using namespace std; // Function to find binomial // coefficient int binomialCoeff( int n, int r) { if (r > n) return 0; long long int m = 1000000007; long long int inv[r + 1] = { 0 }; inv[0] = 1; if (r+1>=2) inv[1] = 1; // Getting the modular inversion // for all the numbers // from 2 to r with respect to m // here m = 1000000007 for ( int i = 2; i <= r; i++) { inv[i] = m - (m / i) * inv[m % i] % m; } int ans = 1; // for 1/(r!) part for ( int i = 2; i <= r; i++) { ans = ((ans % m) * (inv[i] % m)) % m; } // for (n)*(n-1)*(n-2)*...*(n-r+1) part for ( int i = n; i >= (n - r + 1); i--) { ans = ((ans % m) * (i % m)) % m; } return ans; } /* Driver code*/ int main() { int n = 5, r = 2; cout << "Value of C(" << n << ", " << r << ") is " << binomialCoeff(n, r) << endl; return 0; } |
JAVA
// JAVA program for the above approach import java.util.*; class GFG { // Function to find binomial // coefficient static int binomialCoeff( int n, int r) { if (r > n) return 0 ; long m = 1000000007 ; long inv[] = new long [r + 1 ]; inv[ 0 ] = 1 ; if (r+ 1 >= 2 ) inv[ 1 ] = 1 ; // Getting the modular inversion // for all the numbers // from 2 to r with respect to m // here m = 1000000007 for ( int i = 2 ; i <= r; i++) { inv[i] = m - (m / i) * inv[( int ) (m % i)] % m; } int ans = 1 ; // for 1/(r!) part for ( int i = 2 ; i <= r; i++) { ans = ( int ) (((ans % m) * (inv[i] % m)) % m); } // for (n)*(n-1)*(n-2)*...*(n-r+1) part for ( int i = n; i >= (n - r + 1 ); i--) { ans = ( int ) (((ans % m) * (i % m)) % m); } return ans; } /* Driver code*/ public static void main(String[] args) { int n = 5 , r = 2 ; System.out.print( "Value of C(" + n+ ", " + r+ ") is " +binomialCoeff(n, r) + "" ); } } // This code contributed by Rajput-Ji |
Python3
# Python3 program for the above approach # Function to find binomial # coefficient def binomialCoeff(n, r): if (r > n): return 0 m = 1000000007 inv = [ 0 for i in range (r + 1 )] inv[ 0 ] = 1 ; if (r + 1 > = 2 ) inv[ 1 ] = 1 ; # Getting the modular inversion # for all the numbers # from 2 to r with respect to m # here m = 1000000007 for i in range ( 2 , r + 1 ): inv[i] = m - (m / / i) * inv[m % i] % m ans = 1 # for 1/(r!) part for i in range ( 2 , r + 1 ): ans = ((ans % m) * (inv[i] % m)) % m # for (n)*(n-1)*(n-2)*...*(n-r+1) part for i in range (n, n - r, - 1 ): ans = ((ans % m) * (i % m)) % m return ans # Driver code n = 5 r = 2 print ( "Value of C(" ,n , ", " , r , ") is " ,binomialCoeff(n, r)) # This code is contributed by rohan07 |
C#
// C# program for the above approach using System; public class GFG { // Function to find binomial // coefficient static int binomialCoeff( int n, int r) { if (r > n) return 0; long m = 1000000007; long []inv = new long [r + 1]; inv[0] = 1; if (r+1>=2) inv[1] = 1; // Getting the modular inversion // for all the numbers // from 2 to r with respect to m // here m = 1000000007 for ( int i = 2; i <= r; i++) { inv[i] = m - (m / i) * inv[( int ) (m % i)] % m; } int ans = 1; // for 1/(r!) part for ( int i = 2; i <= r; i++) { ans = ( int ) (((ans % m) * (inv[i] % m)) % m); } // for (n)*(n-1)*(n-2)*...*(n-r+1) part for ( int i = n; i >= (n - r + 1); i--) { ans = ( int ) (((ans % m) * (i % m)) % m); } return ans; } /* Driver code*/ public static void Main(String[] args) { int n = 5, r = 2; Console.Write( "Value of C(" + n+ ", " + r+ ") is " +binomialCoeff(n, r) + "" ); } } // This code is contributed by 29AjayKumar |
Javascript
<script> // JavaScript Program for the above approach // Function to find binomial // coefficient function binomialCoeff(n, r) { if (r > n) return 0; let m = 1000000007; let inv = new Array(r + 1).fill(0); inv[0] = 1; if (r + 1 >= 2) inv[1] = 1; // Getting the modular inversion // for all the numbers // from 2 to r with respect to m // here m = 1000000007 for (let i = 2; i <= r; i++) { inv[i] = m - Math.floor(m / i) * inv[m % i] % m; } let ans = 1; // for 1/(r!) part for (let i = 2; i <= r; i++) { ans = ((ans % m) * (inv[i] % m)) % m; } // for (n)*(n-1)*(n-2)*...*(n-r+1) part for (let i = n; i >= (n - r + 1); i--) { ans = ((ans % m) * (i % m)) % m; } return ans; } /* Driver code*/ let n = 5, r = 2; document.write( "Value of C(" + n + ", " + r + ") is " + binomialCoeff(n, r) + "<br>" ); // This code is contributed by Potta Lokesh </script> |
Value of C(5, 2) is 10
时间复杂性: O(n+k)
辅助空间: O(k)
看看这个 时空效率二项式系数
参考资料: http://www.csl.mtu.edu/cs4321/www/Lectures/Lecture%2015%20-%20动态%20编程%20二项式%20系数。htm
https://cp-algorithms.com/algebra/module-inverse.html
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



