给定两个字符串X和Y,打印包含X和Y作为子序列的最短字符串。如果存在多个最短超序列,请打印其中任何一个。 例如:
null
Input: X = "AGGTAB", Y = "GXTXAYB"Output: "AGXGTXAYB" OR "AGGXTXAYB" OR Any string that represents shortestsupersequence of X and YInput: X = "HELLO", Y = "GEEK"Output: "GEHEKLLO" OR "GHEEKLLO"OR Any string that represents shortest supersequence of X and Y
我们已经讨论了如何打印两个给定字符串的最短可能超序列的长度 在这里 .在本文中,我们将打印最短的超序列。 我们已经在前面的文章中讨论了寻找最短超序列长度的算法-
Let X[0..m-1] and Y[0..n-1] be two strings and m and be respective lengths.if (m == 0) return n;if (n == 0) return m;// If last characters are same, then add 1 to result and// recur for X[]if (X[m-1] == Y[n-1]) return 1 + SCS(X, Y, m-1, n-1);// Else find shortest of following two// a) Remove last character from X and recur// b) Remove last character from Y and recurelse return 1 + min( SCS(X, Y, m-1, n), SCS(X, Y, m, n-1) );
下表显示了上述算法遵循的步骤,如果我们使用动态规划以自下而上的方式对其进行求解 字符串X=“AGGTAB”和Y=“GXTXAYB” ,
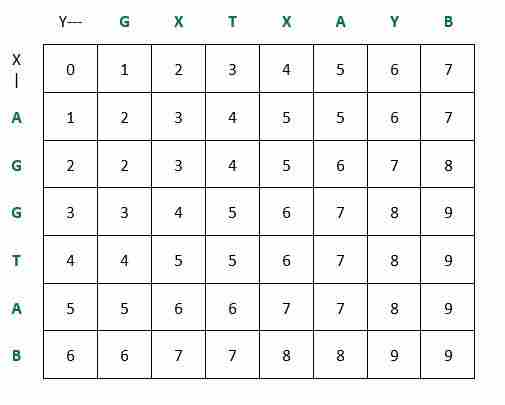
使用DP解矩阵,我们可以通过以下步骤轻松打印两个字符串的最短超序列——
We start from the bottom-right most cell of the matrix and push characters in output string based on below rules- 1. If the characters corresponding to current cell (i, j) in X and Y are same, then the character is part of shortest supersequence. We append it in output string and move diagonally to next cell (i.e. (i - 1, j - 1)). 2. If the characters corresponding to current cell (i, j) in X and Y are different, we have two choices - If matrix[i - 1][j] > matrix[i][j - 1], we add character corresponding to current cell (i, j) in string Y in output string and move to the left cell i.e. (i, j - 1) else we add character corresponding to current cell (i, j) in string X in output string and move to the top cell i.e. (i - 1, j) 3. If string Y reaches its end i.e. j = 0, we add remaining characters of string X in the output string else if string X reaches its end i.e. i = 0, we add remaining characters of string Y in the output string.
以下是上述想法的实施情况——
C++
/* A dynamic programming based C++ program print shortest supersequence of two strings */ #include <bits/stdc++.h> using namespace std; // returns shortest supersequence of X and Y string printShortestSuperSeq(string X, string Y) { int m = X.length(); int n = Y.length(); // dp[i][j] contains length of shortest supersequence // for X[0..i-1] and Y[0..j-1] int dp[m + 1][n + 1]; // Fill table in bottom up manner for ( int i = 0; i <= m; i++) { for ( int j = 0; j <= n; j++) { // Below steps follow recurrence relation if (i == 0) dp[i][j] = j; else if (j == 0) dp[i][j] = i; else if (X[i - 1] == Y[j - 1]) dp[i][j] = 1 + dp[i - 1][j - 1]; else dp[i][j] = 1 + min(dp[i - 1][j], dp[i][j - 1]); } } // Following code is used to print shortest supersequence // dp[m][n] stores the length of the shortest supersequence // of X and Y // string to store the shortest supersequence string str; // Start from the bottom right corner and one by one // push characters in output string int i = m, j = n; while (i > 0 && j > 0) { // If current character in X and Y are same, then // current character is part of shortest supersequence if (X[i - 1] == Y[j - 1]) { // Put current character in result str.push_back(X[i - 1]); // reduce values of i, j and index i--, j--; } // If current character in X and Y are different else if (dp[i - 1][j] > dp[i][j - 1]) { // Put current character of Y in result str.push_back(Y[j - 1]); // reduce values of j and index j--; } else { // Put current character of X in result str.push_back(X[i - 1]); // reduce values of i and index i--; } } // If Y reaches its end, put remaining characters // of X in the result string while (i > 0) { str.push_back(X[i - 1]); i--; } // If X reaches its end, put remaining characters // of Y in the result string while (j > 0) { str.push_back(Y[j - 1]); j--; } // reverse the string and return it reverse(str.begin(), str.end()); return str; } // Driver program to test above function int main() { string X = "AGGTAB" ; string Y = "GXTXAYB" ; cout << printShortestSuperSeq(X, Y); return 0; } |
JAVA
/* A dynamic programming based Java program print shortest supersequence of two strings */ class GFG { // returns shortest supersequence of X and Y static String printShortestSuperSeq(String X, String Y) { int m = X.length(); int n = Y.length(); // dp[i][j] contains length of // shortest supersequence // for X[0..i-1] and Y[0..j-1] int dp[][] = new int [m + 1 ][n + 1 ]; // Fill table in bottom up manner for ( int i = 0 ; i <= m; i++) { for ( int j = 0 ; j <= n; j++) { // Below steps follow recurrence relation if (i == 0 ) { dp[i][j] = j; } else if (j == 0 ) { dp[i][j] = i; } else if (X.charAt(i - 1 ) == Y.charAt(j - 1 )) { dp[i][j] = 1 + dp[i - 1 ][j - 1 ]; } else { dp[i][j] = 1 + Math.min(dp[i - 1 ][j], dp[i][j - 1 ]); } } } // Following code is used to print // shortest supersequence dp[m][n] s // tores the length of the shortest // supersequence of X and Y // string to store the shortest supersequence String str = "" ; // Start from the bottom right corner and one by one // push characters in output string int i = m, j = n; while (i > 0 && j > 0 ) { // If current character in X and Y are same, then // current character is part of shortest supersequence if (X.charAt(i - 1 ) == Y.charAt(j - 1 )) { // Put current character in result str += (X.charAt(i - 1 )); // reduce values of i, j and index i--; j--; } // If current character in X and Y are different else if (dp[i - 1 ][j] > dp[i][j - 1 ]) { // Put current character of Y in result str += (Y.charAt(j - 1 )); // reduce values of j and index j--; } else { // Put current character of X in result str += (X.charAt(i - 1 )); // reduce values of i and index i--; } } // If Y reaches its end, put remaining characters // of X in the result string while (i > 0 ) { str += (X.charAt(i - 1 )); i--; } // If X reaches its end, put remaining characters // of Y in the result string while (j > 0 ) { str += (Y.charAt(j - 1 )); j--; } // reverse the string and return it str = reverse(str); return str; } static String reverse(String input) { char [] temparray = input.toCharArray(); int left, right = 0 ; right = temparray.length - 1 ; for (left = 0 ; left < right; left++, right--) { // Swap values of left and right char temp = temparray[left]; temparray[left] = temparray[right]; temparray[right] = temp; } return String.valueOf(temparray); } // Driver code public static void main(String[] args) { String X = "AGGTAB" ; String Y = "GXTXAYB" ; System.out.println(printShortestSuperSeq(X, Y)); } } // This code is contributed by 29AjayKumar |
Python3
# A dynamic programming based Python3 program print # shortest supersequence of two strings # returns shortest supersequence of X and Y def printShortestSuperSeq(x, y): m = len (x) n = len (y) # dp[i][j] contains length of shortest # supersequence for X[0..i-1] and Y[0..j-1] dp = [[ 0 for i in range (n + 1 )] for j in range (n + 1 )] # Fill table in bottom up manner for i in range (m + 1 ): for j in range (n + 1 ): # Below steps follow recurrence relation if i = = 0 : dp[i][j] = j else if j = = 0 : dp[i][j] = i else if x[i - 1 ] = = y[j - 1 ]: dp[i][j] = 1 + dp[i - 1 ][j - 1 ] else : dp[i][j] = 1 + min (dp[i - 1 ][j], dp[i][j - 1 ]) # Following code is used to print # shortest supersequence # dp[m][n] stores the length of the # shortest supersequence of X and Y # string to store the shortest supersequence string = "" # Start from the bottom right corner and # one by one push characters in output string i = m j = n while i > 0 and j > 0 : # If current character in X and Y are same, # then current character is part of # shortest supersequence if x[i - 1 ] = = y[j - 1 ]: # Put current character in result string + = x[i - 1 ] # reduce values of i, j and index i - = 1 j - = 1 # If current character in X and Y are different elif dp[i - 1 ][j] > dp[i][j - 1 ]: # Put current character of Y in result string + = y[j - 1 ] # reduce values of j and index j - = 1 else : # Put current character of X in result string + = x[i - 1 ] # reduce values of i and index i - = 1 # If Y reaches its end, put remaining characters # of X in the result string while i > 0 : string + = x[i - 1 ] i - = 1 # If X reaches its end, put remaining characters # of Y in the result string while j > 0 : string + = y[j - 1 ] j - = 1 string = list (string) # reverse the string and return it string.reverse() return ''.join(string) # Driver Code if __name__ = = "__main__" : x = "AGGTAB" y = "GXTXAYB" print (printShortestSuperSeq(x, y)) # This code is contributed by # sanjeev2552 |
C#
/* A dynamic programming based C# program print shortest supersequence of two strings */ using System; class GFG { // returns shortest supersequence of X and Y static String printShortestSuperSeq(String X, String Y) { int m = X.Length; int n = Y.Length; // dp[i,j] contains length of // shortest supersequence // for X[0..i-1] and Y[0..j-1] int [,]dp = new int [m + 1, n + 1]; int i, j; // Fill table in bottom up manner for (i = 0; i <= m; i++) { for (j = 0; j <= n; j++) { // Below steps follow recurrence relation if (i == 0) { dp[i, j] = j; } else if (j == 0) { dp[i, j] = i; } else if (X[i - 1] == Y[j - 1]) { dp[i, j] = 1 + dp[i - 1, j - 1]; } else { dp[i, j] = 1 + Math.Min(dp[i - 1, j], dp[i, j - 1]); } } } // Following code is used to print // shortest supersequence dp[m,n] s // tores the length of the shortest // supersequence of X and Y // string to store the shortest supersequence String str = "" ; // Start from the bottom right corner and one by one // push characters in output string i = m; j = n; while (i > 0 && j > 0) { // If current character in X and Y are same, then // current character is part of shortest supersequence if (X[i - 1] == Y[j - 1]) { // Put current character in result str += (X[i - 1]); // reduce values of i, j and index i--; j--; } // If current character in X and Y are different else if (dp[i - 1, j] > dp[i, j - 1]) { // Put current character of Y in result str += (Y[j - 1]); // reduce values of j and index j--; } else { // Put current character of X in result str += (X[i - 1]); // reduce values of i and index i--; } } // If Y reaches its end, put remaining characters // of X in the result string while (i > 0) { str += (X[i - 1]); i--; } // If X reaches its end, put remaining characters // of Y in the result string while (j > 0) { str += (Y[j - 1]); j--; } // reverse the string and return it str = reverse(str); return str; } static String reverse(String input) { char [] temparray = input.ToCharArray(); int left, right = 0; right = temparray.Length - 1; for (left = 0; left < right; left++, right--) { // Swap values of left and right char temp = temparray[left]; temparray[left] = temparray[right]; temparray[right] = temp; } return String.Join( "" ,temparray); } // Driver code public static void Main(String[] args) { String X = "AGGTAB" ; String Y = "GXTXAYB" ; Console.WriteLine(printShortestSuperSeq(X, Y)); } } /* This code has been contributed by PrinciRaj1992*/ |
Javascript
<script> /* A dynamic programming based Javascript program print shortest supersequence of two strings */ // returns shortest supersequence of X and Y function printShortestSuperSeq(X,Y) { let m = X.length; let n = Y.length; // dp[i][j] contains length of // shortest supersequence // for X[0..i-1] and Y[0..j-1] let dp = new Array(m + 1); for (let i=0;i<(m+1);i++) { dp[i]= new Array(n+1); for (let j=0;j<(n+1);j++) dp[i][j]=0; } // Fill table in bottom up manner for (let i = 0; i <= m; i++) { for (let j = 0; j <= n; j++) { // Below steps follow recurrence relation if (i == 0) { dp[i][j] = j; } else if (j == 0) { dp[i][j] = i; } else if (X[i-1] == Y[j-1]) { dp[i][j] = 1 + dp[i - 1][j - 1]; } else { dp[i][j] = 1 + Math.min(dp[i - 1][j], dp[i][j - 1]); } } } // Following code is used to print // shortest supersequence dp[m][n] s // tores the length of the shortest // supersequence of X and Y // string to store the shortest supersequence let str = "" ; // Start from the bottom right corner and one by one // push characters in output string let i = m, j = n; while (i > 0 && j > 0) { // If current character in X and Y are same, then // current character is part of shortest supersequence if (X[i-1] == Y[j-1]) { // Put current character in result str += (X[i-1]); // reduce values of i, j and index i--; j--; } // If current character in X and Y are different else if (dp[i - 1][j] > dp[i][j - 1]) { // Put current character of Y in result str += (Y[j-1]); // reduce values of j and index j--; } else { // Put current character of X in result str += (X[i-1]); // reduce values of i and index i--; } } // If Y reaches its end, put remaining characters // of X in the result string while (i > 0) { str += (X[i-1]); i--; } // If X reaches its end, put remaining characters // of Y in the result string while (j > 0) { str += (Y[j-1]); j--; } // reverse the string and return it str = reverse(str); return str; } function reverse(input) { let temparray = input.split( "" ); let left, right = 0; right = temparray.length - 1; for (left = 0; left < right; left++, right--) { // Swap values of left and right let temp = temparray[left]; temparray[left] = temparray[right]; temparray[right] = temp; } return (temparray).join( "" ); } // Driver code let X = "AGGTAB" ; let Y = "GXTXAYB" ; document.write(printShortestSuperSeq(X, Y)); // This code is contributed by rag2127 </script> |
输出
AGXGTXAYB
时间复杂性 上述溶液的浓度为O(n) 2. ). 辅助空间 程序使用的是O(n) 2. ). 本文由 阿迪蒂亚·戈尔 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



