给定一个文本和一个通配符模式,实现通配符模式匹配算法,查找通配符模式是否与文本匹配。匹配应该覆盖整个文本(而不是部分文本)。 通配符模式可以包含字符“?”还有“*” ‘?’ – 匹配任何单个字符 “*”–匹配任何字符序列(包括空序列)
例如
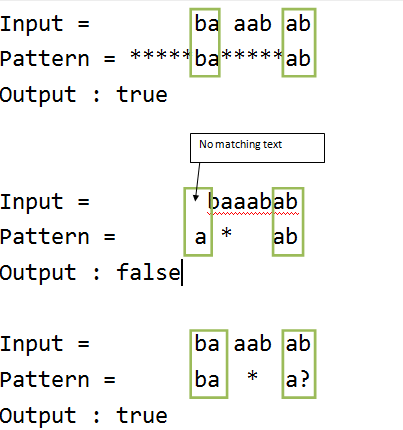
Text = "baaabab",Pattern = “*****ba*****ab", output : truePattern = "baaa?ab", output : truePattern = "ba*a?", output : truePattern = "a*ab", output : false
每次出现“?”通配符模式中的字符可以替换为任何其他字符,而“*”的每次出现都可以替换为一系列字符,这样,替换后的通配符模式就与输入字符串相同。
让我们考虑模式中的任何字符。
案例1:字符为“*” 这里出现了两种情况
- 我们可以忽略“*”字符并移动到模式中的下一个字符。
- “*”字符与文本中的一个或多个字符匹配。这里我们将移动到字符串中的下一个字符。
案例2:角色是“?” 我们可以忽略文本中的当前字符,并移动到模式和文本中的下一个字符。
案例3:该字符不是通配符 如果文本中的当前字符与模式中的当前字符匹配,我们将移动到模式和文本中的下一个字符。如果它们不匹配,则通配符模式和文本不匹配。 我们可以用动态规划来解决这个问题—— 允许 T[i][j] 如果给定字符串中的前i个字符与模式的前j个字符匹配,则为true。
DP初始化:
// both text and pattern are nullT[0][0] = true; // pattern is nullT[i][0] = false; // text is nullT[0][j] = T[0][j - 1] if pattern[j – 1] is '*'
DP关系:
// If current characters match, result is same as // result for lengths minus one. Characters match// in two cases:// a) If pattern character is '?' then it matches // with any character of text. // b) If current characters in both matchif ( pattern[j – 1] == ‘?’) || (pattern[j – 1] == text[i - 1]) T[i][j] = T[i-1][j-1] // If we encounter ‘*’, two choices are possible-// a) We ignore ‘*’ character and move to next // character in the pattern, i.e., ‘*’ // indicates an empty sequence.// b) '*' character matches with ith character in// input else if (pattern[j – 1] == ‘*’) T[i][j] = T[i][j-1] || T[i-1][j] else // if (pattern[j – 1] != text[i - 1]) T[i][j] = false
下面是上述动态规划方法的实现。
C++
// C++ program to implement wildcard // pattern matching algorithm #include <bits/stdc++.h> using namespace std; // Function that matches input str with // given wildcard pattern bool strmatch( char str[], char pattern[], int n, int m) { // empty pattern can only match with // empty string if (m == 0) return (n == 0); // lookup table for storing results of // subproblems bool lookup[n + 1][m + 1]; // initialize lookup table to false memset (lookup, false , sizeof (lookup)); // empty pattern can match with empty string lookup[0][0] = true ; // Only '*' can match with empty string for ( int j = 1; j <= m; j++) if (pattern[j - 1] == '*' ) lookup[0][j] = lookup[0][j - 1]; // fill the table in bottom-up fashion for ( int i = 1; i <= n; i++) { for ( int j = 1; j <= m; j++) { // Two cases if we see a '*' // a) We ignore ‘*’ character and move // to next character in the pattern, // i.e., ‘*’ indicates an empty sequence. // b) '*' character matches with ith // character in input if (pattern[j - 1] == '*' ) lookup[i][j] = lookup[i][j - 1] || lookup[i - 1][j]; // Current characters are considered as // matching in two cases // (a) current character of pattern is '?' // (b) characters actually match else if (pattern[j - 1] == '?' || str[i - 1] == pattern[j - 1]) lookup[i][j] = lookup[i - 1][j - 1]; // If characters don't match else lookup[i][j] = false ; } } return lookup[n][m]; } int main() { char str[] = "baaabab" ; char pattern[] = "*****ba*****ab" ; // char pattern[] = "ba*****ab"; // char pattern[] = "ba*ab"; // char pattern[] = "a*ab"; // char pattern[] = "a*****ab"; // char pattern[] = "*a*****ab"; // char pattern[] = "ba*ab****"; // char pattern[] = "****"; // char pattern[] = "*"; // char pattern[] = "aa?ab"; // char pattern[] = "b*b"; // char pattern[] = "a*a"; // char pattern[] = "baaabab"; // char pattern[] = "?baaabab"; // char pattern[] = "*baaaba*"; if (strmatch(str, pattern, strlen (str), strlen (pattern))) cout << "Yes" << endl; else cout << "No" << endl; return 0; } |
JAVA
// Java program to implement wildcard // pattern matching algorithm import java.util.Arrays; public class GFG { // Function that matches input str with // given wildcard pattern static boolean strmatch(String str, String pattern, int n, int m) { // empty pattern can only match with // empty string if (m == 0 ) return (n == 0 ); // lookup table for storing results of // subproblems boolean [][] lookup = new boolean [n + 1 ][m + 1 ]; // initialize lookup table to false for ( int i = 0 ; i < n + 1 ; i++) Arrays.fill(lookup[i], false ); // empty pattern can match with empty string lookup[ 0 ][ 0 ] = true ; // Only '*' can match with empty string for ( int j = 1 ; j <= m; j++) if (pattern.charAt(j - 1 ) == '*' ) lookup[ 0 ][j] = lookup[ 0 ][j - 1 ]; // fill the table in bottom-up fashion for ( int i = 1 ; i <= n; i++) { for ( int j = 1 ; j <= m; j++) { // Two cases if we see a '*' // a) We ignore '*'' character and move // to next character in the pattern, // i.e., '*' indicates an empty // sequence. // b) '*' character matches with ith // character in input if (pattern.charAt(j - 1 ) == '*' ) lookup[i][j] = lookup[i][j - 1 ] || lookup[i - 1 ][j]; // Current characters are considered as // matching in two cases // (a) current character of pattern is '?' // (b) characters actually match else if (pattern.charAt(j - 1 ) == '?' || str.charAt(i - 1 ) == pattern.charAt(j - 1 )) lookup[i][j] = lookup[i - 1 ][j - 1 ]; // If characters don't match else lookup[i][j] = false ; } } return lookup[n][m]; } // Driver code public static void main(String args[]) { String str = "baaabab" ; String pattern = "*****ba*****ab" ; // String pattern = "ba*****ab"; // String pattern = "ba*ab"; // String pattern = "a*ab"; // String pattern = "a*****ab"; // String pattern = "*a*****ab"; // String pattern = "ba*ab****"; // String pattern = "****"; // String pattern = "*"; // String pattern = "aa?ab"; // String pattern = "b*b"; // String pattern = "a*a"; // String pattern = "baaabab"; // String pattern = "?baaabab"; // String pattern = "*baaaba*"; if (strmatch(str, pattern, str.length(), pattern.length())) System.out.println( "Yes" ); else System.out.println( "No" ); } } // This code is contributed by Sumit Ghosh |
Python3
# Python program to implement wildcard # pattern matching algorithm # Function that matches input strr with # given wildcard pattern def strrmatch(strr, pattern, n, m): # empty pattern can only match with # empty string if (m = = 0 ): return (n = = 0 ) # lookup table for storing results of # subproblems lookup = [[ False for i in range (m + 1 )] for j in range (n + 1 )] # empty pattern can match with empty string lookup[ 0 ][ 0 ] = True # Only '*' can match with empty string for j in range ( 1 , m + 1 ): if (pattern[j - 1 ] = = '*' ): lookup[ 0 ][j] = lookup[ 0 ][j - 1 ] # fill the table in bottom-up fashion for i in range ( 1 , n + 1 ): for j in range ( 1 , m + 1 ): # Two cases if we see a '*' # a) We ignore ‘*’ character and move # to next character in the pattern, # i.e., ‘*’ indicates an empty sequence. # b) '*' character matches with ith # character in input if (pattern[j - 1 ] = = '*' ): lookup[i][j] = lookup[i][j - 1 ] or lookup[i - 1 ][j] # Current characters are considered as # matching in two cases # (a) current character of pattern is '?' # (b) characters actually match else if (pattern[j - 1 ] = = '?' or strr[i - 1 ] = = pattern[j - 1 ]): lookup[i][j] = lookup[i - 1 ][j - 1 ] # If characters don't match else : lookup[i][j] = False return lookup[n][m] # Driver code strr = "baaabab" pattern = "*****ba*****ab" # char pattern[] = "ba*****ab" # char pattern[] = "ba*ab" # char pattern[] = "a*ab" # char pattern[] = "a*****ab" # char pattern[] = "*a*****ab" # char pattern[] = "ba*ab****" # char pattern[] = "****" # char pattern[] = "*" # char pattern[] = "aa?ab" # char pattern[] = "b*b" # char pattern[] = "a*a" # char pattern[] = "baaabab" # char pattern[] = "?baaabab" # char pattern[] = "*baaaba*" if (strrmatch(strr, pattern, len (strr), len (pattern))): print ( "Yes" ) else : print ( "No" ) # This code is contributed by shubhamsingh10 |
C#
// C# program to implement wildcard // pattern matching algorithm using System; class GFG { // Function that matches input str with // given wildcard pattern static Boolean strmatch(String str, String pattern, int n, int m) { // empty pattern can only match with // empty string if (m == 0) return (n == 0); // lookup table for storing results of // subproblems Boolean[, ] lookup = new Boolean[n + 1, m + 1]; // initialize lookup table to false for ( int i = 0; i < n + 1; i++) for ( int j = 0; j < m + 1; j++) lookup[i, j] = false ; // empty pattern can match with // empty string lookup[0, 0] = true ; // Only '*' can match with empty string for ( int j = 1; j <= m; j++) if (pattern[j - 1] == '*' ) lookup[0, j] = lookup[0, j - 1]; // fill the table in bottom-up fashion for ( int i = 1; i <= n; i++) { for ( int j = 1; j <= m; j++) { // Two cases if we see a '*' // a) We ignore '*'' character and move // to next character in the pattern, // i.e., '*' indicates an empty // sequence. // b) '*' character matches with ith // character in input if (pattern[j - 1] == '*' ) lookup[i, j] = lookup[i, j - 1] || lookup[i - 1, j]; // Current characters are considered as // matching in two cases // (a) current character of pattern is '?' // (b) characters actually match else if (pattern[j - 1] == '?' || str[i - 1] == pattern[j - 1]) lookup[i, j] = lookup[i - 1, j - 1]; // If characters don't match else lookup[i, j] = false ; } } return lookup[n, m]; } // Driver Code public static void Main(String[] args) { String str = "baaabab" ; String pattern = "*****ba*****ab" ; // String pattern = "ba*****ab"; // String pattern = "ba*ab"; // String pattern = "a*ab"; // String pattern = "a*****ab"; // String pattern = "*a*****ab"; // String pattern = "ba*ab****"; // String pattern = "****"; // String pattern = "*"; // String pattern = "aa?ab"; // String pattern = "b*b"; // String pattern = "a*a"; // String pattern = "baaabab"; // String pattern = "?baaabab"; // String pattern = "*baaaba*"; if (strmatch(str, pattern, str.Length, pattern.Length)) Console.WriteLine( "Yes" ); else Console.WriteLine( "No" ); } } // This code is contributed by Rajput-Ji |
Yes
时间复杂性: O(m x n) 辅助空间: O(m x n)
DP回忆录解决方案:-
C++
// C++ program to implement wildcard // pattern matching algorithm #include <bits/stdc++.h> using namespace std; // Function that matches input str with // given wildcard pattern vector<vector< int > > dp; int finding(string& s, string& p, int n, int m) { // return 1 if n and m are negative if (n < 0 && m < 0) return 1; // return 0 if m is negative if (m < 0) return 0; // return n if n is negative if (n < 0) { // while m is positive while (m >= 0) { if (p[m] != '*' ) return 0; m--; } return 1; } // if dp state is not visited if (dp[n][m] == -1) { if (p[m] == '*' ) { return dp[n][m] = finding(s, p, n - 1, m) || finding(s, p, n, m - 1); } else { if (p[m] != s[n] && p[m] != '?' ) return dp[n][m] = 0; else return dp[n][m] = finding(s, p, n - 1, m - 1); } } // return dp[n][m] if dp state is previsited return dp[n][m]; } bool isMatch(string s, string p) { dp.clear(); // resize the dp array dp.resize(s.size() + 1, vector< int >(p.size() + 1, -1)); return dp[s.size()][p.size()] = finding(s, p, s.size() - 1, p.size() - 1); } // Driver code int main() { string str = "baaabab" ; string pattern = "*****ba*****ab" ; // char pattern[] = "ba*****ab"; // char pattern[] = "ba*ab"; // char pattern[] = "a*ab"; // char pattern[] = "a*****ab"; // char pattern[] = "*a*****ab"; // char pattern[] = "ba*ab****"; // char pattern[] = "****"; // char pattern[] = "*"; // char pattern[] = "aa?ab"; // char pattern[] = "b*b"; // char pattern[] = "a*a"; // char pattern[] = "baaabab"; // char pattern[] = "?baaabab"; // char pattern[] = "*baaaba*"; if (isMatch(str, pattern)) cout << "Yes" << endl; else cout << "No" << endl; return 0; } |
Yes
时间复杂性 :O(m×n)。 辅助空间: O(m×n)。
进一步改进: 我们可以利用只使用最后一行的结果这一事实来提高空间复杂度。 还有一个改进是,可以将模式中连续的“*”合并为单个“*”,因为它们的意思相同。例如,对于模式“****ba****ab”,如果我们合并连续的星星,结果字符串将是“*ba*ab”。所以,m的值从14减少到6。 本文由 阿迪蒂亚·戈尔 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以写一篇文章,然后将文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



