先决条件: 生命周期评价基础 , 基于秩和路径压缩的不相交集并 我们得到一棵树(可以扩展为DAG),我们有许多形式为LCA(u,v)的查询,即查找节点“u”和“v”的LCA。 我们可以在中执行这些查询 O(N+QlogN)时间 使用RMQ ,其中O(N)时间用于预处理,O(logn)时间用于回答查询,其中 N=节点数和 Q=需要回答的问题数量。 我们能做得更好吗?我们能在线性(几乎)时间内完成吗?对 本文介绍了一种离线算法,该算法以大约10分钟的时间执行这些查询 O(N+Q)时间 尽管如此,这并不完全是线性的,因为时间复杂度分析中涉及到一个逆阿克曼函数。有关逆阿克曼函数的更多详细信息,请参阅 这 .作为总结,我们可以说,对于可以写入物理逆的任何输入大小值,逆阿克曼函数仍然小于4。因此,我们认为这几乎是线性的。 我们考虑输入树如下所示。我们将 预处理 树和填充两个数组- 孩子和兄弟姐妹 根据下面的解释-
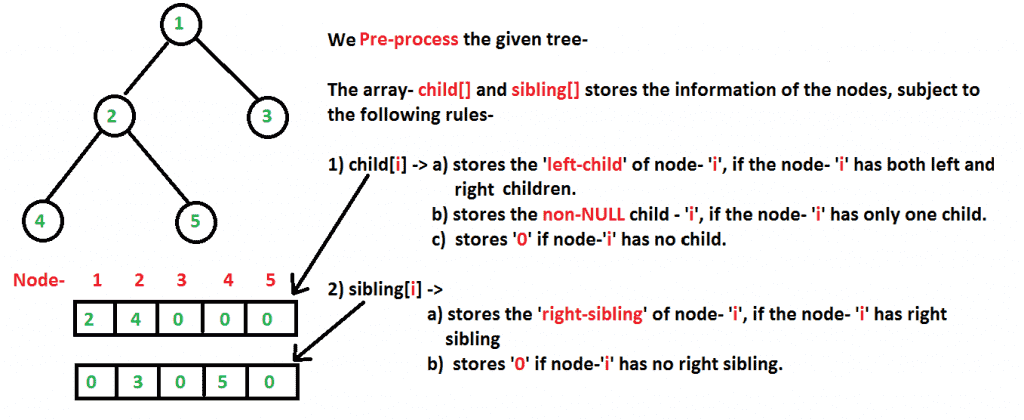
让我们来处理这些查询- 生命周期评价(5,4),生命周期评价(1,3),生命周期评价(2,3) 现在,在预处理之后,我们执行 LCA步行 从树的根开始(这里是节点“1”)。但在LCA步行之前,我们用 白色 .在整个LCA过程中,我们使用了三个不相交的集合并集函数——makeSet()、findSet()、unionSet()。 这些函数使用按秩合并和路径压缩技术来提高运行时间。在生命周期评估过程中,我们的查询会得到处理和输出(以随机顺序)。在对整棵树进行LCA遍历后,所有节点都会着色 黑色 . Tarjan离线LCA算法步骤摘自CLRS,第21-3节,第584页,第2/3版。

注意:查询可能不会按原始顺序处理。我们可以很容易地修改流程,并根据输入顺序对其进行排序。 下面的图片清楚地描述了发生的所有步骤。红色箭头表示我们的旅行方向 递归函数LCA() .
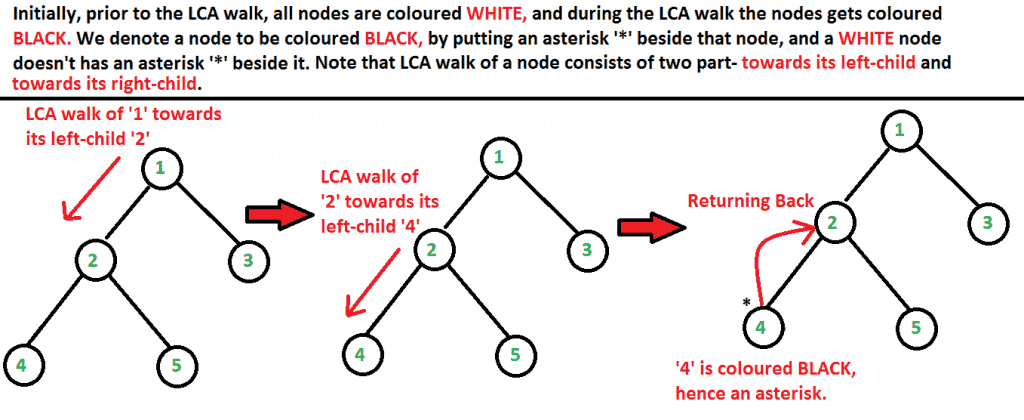
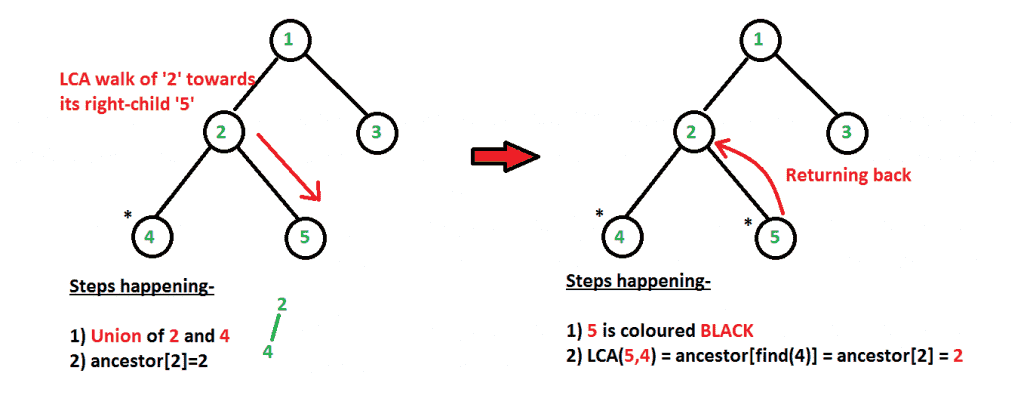

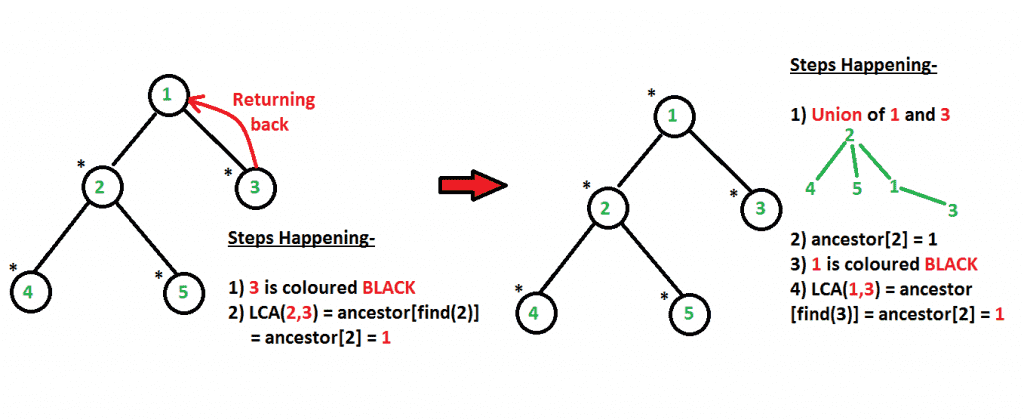
从上面的图片中,我们可以清楚地看到,查询是按照以下顺序处理的:LCA(5,4)、LCA(2,3)、LCA(1,3),它们与输入的顺序不同(LCA(5,4)、LCA(1,3)、LCA(2,3))。
以下是上述方法的实施情况:
C++
// A C++ Program to implement Tarjan Offline LCA Algorithm #include <bits/stdc++.h> #define V 5 // number of nodes in input tree #define WHITE 1 // COLOUR 'WHITE' is assigned value 1 #define BLACK 2 // COLOUR 'BLACK' is assigned value 2 /* A binary tree node has data, pointer to left child and a pointer to right child */ struct Node { int data; Node* left, *right; }; /* subset[i].parent-->Holds the parent of node-'i' subset[i].rank-->Holds the rank of node-'i' subset[i].ancestor-->Holds the LCA queries answers subset[i].child-->Holds one of the child of node-'i' if present, else -'0' subset[i].sibling-->Holds the right-sibling of node-'i' if present, else -'0' subset[i].color-->Holds the colour of node-'i' */ struct subset { int parent, rank, ancestor, child, sibling, color; }; // Structure to represent a query // A query consists of (L,R) and we will process the // queries offline a/c to Tarjan's offline LCA algorithm struct Query { int L, R; }; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ Node* newNode( int data) { Node* node = new Node; node->data = data; node->left = node->right = NULL; return (node); } //A utility function to make set void makeSet( struct subset subsets[], int i) { if (i < 1 || i > V) return ; subsets[i].color = WHITE; subsets[i].parent = i; subsets[i].rank = 0; return ; } // A utility function to find set of an element i // (uses path compression technique) int findSet( struct subset subsets[], int i) { // find root and make root as parent of i (path compression) if (subsets[i].parent != i) subsets[i].parent = findSet (subsets, subsets[i].parent); return subsets[i].parent; } // A function that does union of two sets of x and y // (uses union by rank) void unionSet( struct subset subsets[], int x, int y) { int xroot = findSet (subsets, x); int yroot = findSet (subsets, y); // Attach smaller rank tree under root of high rank tree // (Union by Rank) if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot; // If ranks are same, then make one as root and increment // its rank by one else { subsets[yroot].parent = xroot; (subsets[xroot].rank)++; } } // The main function that prints LCAs. u is root's data. // m is size of q[] void lcaWalk( int u, struct Query q[], int m, struct subset subsets[]) { // Make Sets makeSet(subsets, u); // Initially, each node's ancestor is the node // itself. subsets[findSet(subsets, u)].ancestor = u; int child = subsets[u].child; // This while loop doesn't run for more than 2 times // as there can be at max. two children of a node while (child != 0) { lcaWalk(child, q, m, subsets); unionSet (subsets, u, child); subsets[findSet(subsets, u)].ancestor = u; child = subsets[child].sibling; } subsets[u].color = BLACK; for ( int i = 0; i < m; i++) { if (q[i].L == u) { if (subsets[q[i].R].color == BLACK) { printf ( "LCA(%d %d) -> %d" , q[i].L, q[i].R, subsets[findSet(subsets,q[i].R)].ancestor); } } else if (q[i].R == u) { if (subsets[q[i].L].color == BLACK) { printf ( "LCA(%d %d) -> %d" , q[i].L, q[i].R, subsets[findSet(subsets,q[i].L)].ancestor); } } } return ; } // This is basically an inorder traversal and // we preprocess the arrays-> child[] // and sibling[] in "struct subset" with // the tree structure using this function. void preprocess(Node * node, struct subset subsets[]) { if (node == NULL) return ; // Recur on left child preprocess(node->left, subsets); if (node->left != NULL&&node->right != NULL) { /* Note that the below two lines can also be this- subsets[node->data].child = node->right->data; subsets[node->right->data].sibling = node->left->data; This is because if both left and right children of node-'i' are present then we can store any of them in subsets[i].child and correspondingly its sibling*/ subsets[node->data].child = node->left->data; subsets[node->left->data].sibling = node->right->data; } else if ((node->left != NULL && node->right == NULL) || (node->left == NULL && node->right != NULL)) { if (node->left != NULL && node->right == NULL) subsets[node->data].child = node->left->data; else subsets[node->data].child = node->right->data; } //Recur on right child preprocess (node->right, subsets); } // A function to initialise prior to pre-processing and // LCA walk void initialise( struct subset subsets[]) { // Initialising the structure with 0's memset (subsets, 0, (V+1) * sizeof ( struct subset)); // We colour all nodes WHITE before LCA Walk. for ( int i=1; i<=V; i++) subsets[i].color=WHITE; return ; } // Prints LCAs for given queries q[0..m-1] in a tree // with given root void printLCAs(Node *root, Query q[], int m) { // Allocate memory for V subsets and nodes struct subset * subsets = new subset[V+1]; // Creates subsets and colors them WHITE initialise(subsets); // Preprocess the tree preprocess(root, subsets); // Perform a tree walk to process the LCA queries // offline lcaWalk(root->data , q, m, subsets); } // Driver program to test above functions int main() { /* We construct a binary tree :- 1 / 2 3 / 4 5 */ Node *root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); // LCA Queries to answer Query q[] = {{5, 4}, {1, 3}, {2, 3}}; int m = sizeof (q)/ sizeof (q[0]); printLCAs(root, q, m); return 0; } |
JAVA
// A Java Program to implement Tarjan Offline LCA Algorithm import java.util.Arrays; class GFG { static final int V = 5 ; // number of nodes in input tree static final int WHITE = 1 ; // COLOUR 'WHITE' is assigned value 1 static final int BLACK = 2 ; // COLOUR 'BLACK' is assigned value 2 /* A binary tree node has data, pointer to left child and a pointer to right child */ static class Node { int data; Node left, right; }; /* subset[i].parent-.Holds the parent of node-'i' subset[i].rank-.Holds the rank of node-'i' subset[i].ancestor-.Holds the LCA queries answers subset[i].child-.Holds one of the child of node-'i' if present, else -'0' subset[i].sibling-.Holds the right-sibling of node-'i' if present, else -'0' subset[i].color-.Holds the colour of node-'i' */ static class subset { int parent; int rank; int ancestor; int child; int sibling; int color; }; // Structure to represent a query // A query consists of (L,R) and we will process the // queries offline a/c to Tarjan's offline LCA algorithm static class Query { int L, R; Query( int L, int R) { this .L = L; this .R = R; } }; /* Helper function that allocates a new node with the given data and null left and right pointers. */ static Node newNode( int data) { Node node = new Node(); node.data = data; node.left = node.right = null ; return (node); } // A utility function to make set static void makeSet(subset subsets[], int i) { if (i < 1 || i > V) return ; subsets[i].color = WHITE; subsets[i].parent = i; subsets[i].rank = 0 ; return ; } // A utility function to find set of an element i // (uses path compression technique) static int findSet(subset subsets[], int i) { // find root and make root as parent of i (path compression) if (subsets[i].parent != i) subsets[i].parent = findSet (subsets, subsets[i].parent); return subsets[i].parent; } // A function that does union of two sets of x and y // (uses union by rank) static void unionSet(subset subsets[], int x, int y) { int xroot = findSet (subsets, x); int yroot = findSet (subsets, y); // Attach smaller rank tree under root of high rank tree // (Union by Rank) if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot; // If ranks are same, then make one as root and increment // its rank by one else { subsets[yroot].parent = xroot; (subsets[xroot].rank)++; } } // The main function that prints LCAs. u is root's data. // m is size of q[] static void lcaWalk( int u, Query q[], int m, subset subsets[]) { // Make Sets makeSet(subsets, u); // Initially, each node's ancestor is the node // itself. subsets[findSet(subsets, u)].ancestor = u; int child = subsets[u].child; // This while loop doesn't run for more than 2 times // as there can be at max. two children of a node while (child != 0 ) { lcaWalk(child, q, m, subsets); unionSet (subsets, u, child); subsets[findSet(subsets, u)].ancestor = u; child = subsets[child].sibling; } subsets[u].color = BLACK; for ( int i = 0 ; i < m; i++) { if (q[i].L == u) { if (subsets[q[i].R].color == BLACK) { System.out.printf( "LCA(%d %d)->%d" , q[i].L, q[i].R, subsets[findSet(subsets,q[i].R)].ancestor); } } else if (q[i].R == u) { if (subsets[q[i].L].color == BLACK) { System.out.printf( "LCA(%d %d)->%d" , q[i].L, q[i].R, subsets[findSet(subsets,q[i].L)].ancestor); } } } return ; } // This is basically an inorder traversal and // we preprocess the arrays. child[] // and sibling[] in "subset" with // the tree structure using this function. static void preprocess(Node node, subset subsets[]) { if (node == null ) return ; // Recur on left child preprocess(node.left, subsets); if (node.left != null && node.right != null ) { /* Note that the below two lines can also be this- subsets[node.data].child = node.right.data; subsets[node.right.data].sibling = node.left.data; This is because if both left and right children of node-'i' are present then we can store any of them in subsets[i].child and correspondingly its sibling*/ subsets[node.data].child = node.left.data; subsets[node.left.data].sibling = node.right.data; } else if ((node.left != null && node.right == null ) || (node.left == null && node.right != null )) { if (node.left != null && node.right == null ) subsets[node.data].child = node.left.data; else subsets[node.data].child = node.right.data; } // Recur on right child preprocess (node.right, subsets); } // A function to initialise prior to pre-processing and // LCA walk static void initialise(subset subsets[]) { // We colour all nodes WHITE before LCA Walk. for ( int i = 1 ; i < subsets.length; i++) { subsets[i] = new subset(); subsets[i].color = WHITE; } return ; } // Prints LCAs for given queries q[0..m-1] in a tree // with given root static void printLCAs(Node root, Query q[], int m) { // Allocate memory for V subsets and nodes subset []subsets = new subset[V + 1 ]; // Creates subsets and colors them WHITE initialise(subsets); // Preprocess the tree preprocess(root, subsets); // Perform a tree walk to process the LCA queries // offline lcaWalk(root.data , q, m, subsets); } // Driver code public static void main(String[] args) { /* We construct a binary tree :- 1 / 2 3 / 4 5 */ Node root = newNode( 1 ); root.left = newNode( 2 ); root.right = newNode( 3 ); root.left.left = newNode( 4 ); root.left.right = newNode( 5 ); // LCA Queries to answer Query q[] = new Query[ 3 ]; q[ 0 ] = new Query( 5 , 4 ); q[ 1 ] = new Query( 1 , 3 ); q[ 2 ] = new Query( 2 , 3 ); int m = q.length; printLCAs(root, q, m); } } // This code is contributed by gauravrajput1 |
Python3
# A Python3 program to implement Tarjan # Offline LCA Algorithm # Number of nodes in input tree V = 5 # COLOUR 'WHITE' is assigned value 1 WHITE = 1 # COLOUR 'BLACK' is assigned value 2 BLACK = 2 # A binary tree node has data, pointer # to left child and a pointer to right child class Node: def __init__( self ): self .data = 0 self .left = None self .right = None ''' subset[i].parent-.Holds the parent of node-'i' subset[i].rank-.Holds the rank of node-'i' subset[i].ancestor-.Holds the LCA queries answers subset[i].child-.Holds one of the child of node-'i' if present, else -'0' subset[i].sibling-.Holds the right-sibling of node-'i' if present, else -'0' subset[i].color-.Holds the colour of node-'i' ''' class subset: def __init__( self ): self .parent = 0 self .rank = 0 self .ancestor = 0 self .child = 0 self .sibling = 0 self .color = 0 # Structure to represent a query # A query consists of (L,R) and we # will process the queries offline # a/c to Tarjan's offline LCA algorithm class Query: def __init__( self , L, R): self .L = L self .R = R # Helper function that allocates a new node # with the given data and None left and # right pointers. def newNode(data): node = Node() node.data = data node.left = node.right = None return (node) # A utility function to make set def makeSet(subsets, i): if (i < 1 or i > V): return subsets[i].color = WHITE subsets[i].parent = i subsets[i].rank = 0 return # A utility function to find set of an element i # (uses path compression technique) def findSet(subsets, i): # Find root and make root as parent # of i (path compression) if (subsets[i].parent ! = i): subsets[i].parent = findSet(subsets, subsets[i].parent) return subsets[i].parent # A function that does union of two sets # of x and y (uses union by rank) def unionSet(subsets, x, y): xroot = findSet(subsets, x) yroot = findSet(subsets, y) # Attach smaller rank tree under root of # high rank tree (Union by Rank) if (subsets[xroot].rank < subsets[yroot].rank): subsets[xroot].parent = yroot else if (subsets[xroot].rank > subsets[yroot].rank): subsets[yroot].parent = xroot # If ranks are same, then make one as root # and increment its rank by one else : subsets[yroot].parent = xroot (subsets[xroot].rank) + = 1 # The main function that prints LCAs. u is # root's data. m is size of q[] def lcaWalk(u, q, m, subsets): # Make Sets makeSet(subsets, u) # Initially, each node's ancestor is the node # itself. subsets[findSet(subsets, u)].ancestor = u child = subsets[u].child # This while loop doesn't run for more than 2 times # as there can be at max. two children of a node while (child ! = 0 ): lcaWalk(child, q, m, subsets) unionSet(subsets, u, child) subsets[findSet(subsets, u)].ancestor = u child = subsets[child].sibling subsets[u].color = BLACK for i in range (m): if (q[i].L = = u): if (subsets[q[i].R].color = = BLACK): print ( "LCA(%d %d) -> %d" % (q[i].L, q[i].R, subsets[findSet(subsets, q[i].R)].ancestor)) else if (q[i].R = = u): if (subsets[q[i].L].color = = BLACK): print ( "LCA(%d %d) -> %d" % (q[i].L, q[i].R, subsets[findSet(subsets, q[i].L)].ancestor)) return # This is basically an inorder traversal and # we preprocess the arrays. child[] # and sibling[] in "struct subset" with # the tree structure using this function. def preprocess(node, subsets): if (node = = None ): return # Recur on left child preprocess(node.left, subsets) if (node.left ! = None and node.right ! = None ): ''' Note that the below two lines can also be this- subsets[node.data].child = node.right.data; subsets[node.right.data].sibling = node.left.data; This is because if both left and right children of node-'i' are present then we can store any of them in subsets[i].child and correspondingly its sibling''' subsets[node.data].child = node.left.data subsets[node.left.data].sibling = node.right.data else if ((node.left ! = None and node.right = = None ) or (node.left = = None and node.right ! = None )): if (node.left ! = None and node.right = = None ): subsets[node.data].child = node.left.data else : subsets[node.data].child = node.right.data # Recur on right child preprocess(node.right, subsets) # A function to initialise prior to pre-processing and # LCA walk def initialise(subsets): # Initialising the structure with 0's # memset(subsets, 0, (V+1) * sizeof(struct subset)); # We colour all nodes WHITE before LCA Walk. for i in range ( 1 , V + 1 ): subsets[i].color = WHITE return # Prints LCAs for given queries q[0..m-1] in a tree # with given root def printLCAs(root, q, m): # Allocate memory for V subsets and nodes subsets = [subset() for _ in range (V + 1 )] # Creates subsets and colors them WHITE initialise(subsets) # Preprocess the tree preprocess(root, subsets) # Perform a tree walk to process the LCA queries # offline lcaWalk(root.data, q, m, subsets) # Driver code if __name__ = = "__main__" : ''' We construct a binary tree :- 1 / 2 3 / 4 5 ''' root = newNode( 1 ) root.left = newNode( 2 ) root.right = newNode( 3 ) root.left.left = newNode( 4 ) root.left.right = newNode( 5 ) # LCA Queries to answer q = [Query( 5 , 4 ), Query( 1 , 3 ), Query( 2 , 3 )] m = len (q) printLCAs(root, q, m) # This code is contributed by sanjeev2552 |
C#
// A C# Program to implement Tarjan Offline LCA Algorithm using System; public class GFG { static readonly int V = 5; // number of nodes in input tree static readonly int WHITE = 1; // COLOUR 'WHITE' is assigned value 1 static readonly int BLACK = 2; // COLOUR 'BLACK' is assigned value 2 /* A binary tree node has data, pointer to left child and a pointer to right child */ public class Node { public int data; public Node left, right; }; /* subset[i].parent-.Holds the parent of node-'i' subset[i].rank-.Holds the rank of node-'i' subset[i].ancestor-.Holds the LCA queries answers subset[i].child-.Holds one of the child of node-'i' if present, else -'0' subset[i].sibling-.Holds the right-sibling of node-'i' if present, else -'0' subset[i].color-.Holds the colour of node-'i' */ public class subset { public int parent; public int rank; public int ancestor; public int child; public int sibling; public int color; }; // Structure to represent a query // A query consists of (L,R) and we will process the // queries offline a/c to Tarjan's offline LCA algorithm public class Query { public int L, R; public Query( int L, int R) { this .L = L; this .R = R; } }; /* Helper function that allocates a new node with the given data and null left and right pointers. */ static Node newNode( int data) { Node node = new Node(); node.data = data; node.left = node.right = null ; return (node); } // A utility function to make set static void makeSet(subset []subsets, int i) { if (i < 1 || i > V) return ; subsets[i].color = WHITE; subsets[i].parent = i; subsets[i].rank = 0; return ; } // A utility function to find set of an element i // (uses path compression technique) static int findSet(subset []subsets, int i) { // find root and make root as parent of i (path compression) if (subsets[i].parent != i) subsets[i].parent = findSet (subsets, subsets[i].parent); return subsets[i].parent; } // A function that does union of two sets of x and y // (uses union by rank) static void unionSet(subset []subsets, int x, int y) { int xroot = findSet (subsets, x); int yroot = findSet (subsets, y); // Attach smaller rank tree under root of high rank tree // (Union by Rank) if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot; // If ranks are same, then make one as root and increment // its rank by one else { subsets[yroot].parent = xroot; (subsets[xroot].rank)++; } } // The main function that prints LCAs. u is root's data. // m is size of q[] static void lcaWalk( int u, Query []q, int m, subset []subsets) { // Make Sets makeSet(subsets, u); // Initially, each node's ancestor is the node // itself. subsets[findSet(subsets, u)].ancestor = u; int child = subsets[u].child; // This while loop doesn't run for more than 2 times // as there can be at max. two children of a node while (child != 0) { lcaWalk(child, q, m, subsets); unionSet (subsets, u, child); subsets[findSet(subsets, u)].ancestor = u; child = subsets[child].sibling; } subsets[u].color = BLACK; for ( int i = 0; i < m; i++) { if (q[i].L == u) { if (subsets[q[i].R].color == BLACK) { Console.WriteLine( "LCA(" + q[i].L + " " + q[i].R+ ") -> " + subsets[findSet(subsets, q[i].R)].ancestor); } } else if (q[i].R == u) { if (subsets[q[i].L].color == BLACK) { Console.WriteLine( "LCA(" + q[i].L + " " + q[i].R + ") -> " + subsets[findSet(subsets, q[i].L)].ancestor); } } } return ; } // This is basically an inorder traversal and // we preprocess the arrays. child[] // and sibling[] in "subset" with // the tree structure using this function. static void preprocess(Node node, subset []subsets) { if (node == null ) return ; // Recur on left child preprocess(node.left, subsets); if (node.left != null && node.right != null ) { /* Note that the below two lines can also be this- subsets[node.data].child = node.right.data; subsets[node.right.data].sibling = node.left.data; This is because if both left and right children of node-'i' are present then we can store any of them in subsets[i].child and correspondingly its sibling*/ subsets[node.data].child = node.left.data; subsets[node.left.data].sibling = node.right.data; } else if ((node.left != null && node.right == null ) || (node.left == null && node.right != null )) { if (node.left != null && node.right == null ) subsets[node.data].child = node.left.data; else subsets[node.data].child = node.right.data; } // Recur on right child preprocess (node.right, subsets); } // A function to initialise prior to pre-processing and // LCA walk static void initialise(subset []subsets) { // We colour all nodes WHITE before LCA Walk. for ( int i = 1; i < subsets.Length; i++) { subsets[i] = new subset(); subsets[i].color = WHITE; } return ; } // Prints LCAs for given queries q[0..m-1] in a tree // with given root static void printLCAs(Node root, Query []q, int m) { // Allocate memory for V subsets and nodes subset []subsets = new subset[V + 1]; // Creates subsets and colors them WHITE initialise(subsets); // Preprocess the tree preprocess(root, subsets); // Perform a tree walk to process the LCA queries // offline lcaWalk(root.data, q, m, subsets); } // Driver code public static void Main(String[] args) { /* We construct a binary tree :- 1 / 2 3 / 4 5 */ Node root = newNode(1); root.left = newNode(2); root.right = newNode(3); root.left.left = newNode(4); root.left.right = newNode(5); // LCA Queries to answer Query []q = new Query[3]; q[0] = new Query(5, 4); q[1] = new Query(1, 3); q[2] = new Query(2, 3); int m = q.Length; printLCAs(root, q, m); } } // This code is contributed by Rajput-Ji |
Javascript
<script> // A Javascript Program to implement Tarjan Offline LCA Algorithm let V = 5; // number of nodes in input tree let WHITE = 1; // COLOUR 'WHITE' is assigned value 1 let BLACK = 2; // COLOUR 'BLACK' is assigned value 2 /* A binary tree node has data, pointer to left child and a pointer to right child */ class Node { constructor(data) { this .data = data; this .left = this .right = null ; } } /* subset[i].parent-.Holds the parent of node-'i' subset[i].rank-.Holds the rank of node-'i' subset[i].ancestor-.Holds the LCA queries answers subset[i].child-.Holds one of the child of node-'i' if present, else -'0' subset[i].sibling-.Holds the right-sibling of node-'i' if present, else -'0' subset[i].color-.Holds the colour of node-'i' */ class subset { constructor() { this .parent = 0; this .rank = 0; this .ancestor = 0; this .child = 0; this .sibling = 0; this .color = 0; } } // Structure to represent a query // A query consists of (L,R) and we will process the // queries offline a/c to Tarjan's offline LCA algorithm class Query { constructor(L, R) { this .L = L; this .R = R; } } /* Helper function that allocates a new node with the given data and null left and right pointers. */ function newNode(data) { let node = new Node(); node.data = data; node.left = node.right = null ; return (node); } // A utility function to make set function makeSet(subsets,i) { if (i < 1 || i > V) return ; subsets[i].color = WHITE; subsets[i].parent = i; subsets[i].rank = 0; return ; } // A utility function to find set of an element i // (uses path compression technique) function findSet(subsets, i) { // find root and make root as parent of i (path compression) if (subsets[i].parent != i) subsets[i].parent = findSet (subsets, subsets[i].parent); return subsets[i].parent; } // A function that does union of two sets of x and y // (uses union by rank) function unionSet(subsets, x, y) { let xroot = findSet (subsets, x); let yroot = findSet (subsets, y); // Attach smaller rank tree under root of high rank tree // (Union by Rank) if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot; // If ranks are same, then make one as root and increment // its rank by one else { subsets[yroot].parent = xroot; (subsets[xroot].rank)++; } } // The main function that prints LCAs. u is root's data. // m is size of q[] function lcaWalk(u,q,m,subsets) { // Make Sets makeSet(subsets, u); // Initially, each node's ancestor is the node // itself. subsets[findSet(subsets, u)].ancestor = u; let child = subsets[u].child; // This while loop doesn't run for more than 2 times // as there can be at max. two children of a node while (child != 0) { lcaWalk(child, q, m, subsets); unionSet (subsets, u, child); subsets[findSet(subsets, u)].ancestor = u; child = subsets[child].sibling; } subsets[u].color = BLACK; for (let i = 0; i < m; i++) { if (q[i].L == u) { if (subsets[q[i].R].color == BLACK) { document.write( "LCA(" + q[i].L+ " " +q[i].R+ ") -> " ,subsets[findSet(subsets,q[i].R)].ancestor+ "<br>" ); } } else if (q[i].R == u) { if (subsets[q[i].L].color == BLACK) { document.write( "LCA(" + q[i].L+ " " +q[i].R+ ") -> " ,subsets[findSet(subsets,q[i].L)].ancestor+ "<br>" ); } } } return ; } // This is basically an inorder traversal and // we preprocess the arrays. child[] // and sibling[] in "subset" with // the tree structure using this function. function preprocess(node,subsets) { if (node == null ) return ; // Recur on left child preprocess(node.left, subsets); if (node.left != null && node.right != null ) { /* Note that the below two lines can also be this- subsets[node.data].child = node.right.data; subsets[node.right.data].sibling = node.left.data; This is because if both left and right children of node-'i' are present then we can store any of them in subsets[i].child and correspondingly its sibling*/ subsets[node.data].child = node.left.data; subsets[node.left.data].sibling = node.right.data; } else if ((node.left != null && node.right == null ) || (node.left == null && node.right != null )) { if (node.left != null && node.right == null ) subsets[node.data].child = node.left.data; else subsets[node.data].child = node.right.data; } // Recur on right child preprocess (node.right, subsets); } // A function to initialise prior to pre-processing and // LCA walk function initialise(subsets) { // We colour all nodes WHITE before LCA Walk. for (let i = 1; i < subsets.length; i++) { subsets[i] = new subset(); subsets[i].color = WHITE; } return ; } // Prints LCAs for given queries q[0..m-1] in a tree // with given root function printLCAs(root, q, m) { // Allocate memory for V subsets and nodes let subsets = new Array(V + 1); // Creates subsets and colors them WHITE initialise(subsets); // Preprocess the tree preprocess(root, subsets); // Perform a tree walk to process the LCA queries // offline lcaWalk(root.data , q, m, subsets); } // Driver code /* We construct a binary tree :- 1 / 2 3 / 4 5 */ let root = newNode(1); root.left = newNode(2); root.right = newNode(3); root.left.left = newNode(4); root.left.right = newNode(5); // LCA Queries to answer let q = new Array(3); q[0] = new Query(5, 4); q[1] = new Query(1, 3); q[2] = new Query(2, 3); let m = q.length; printLCAs(root, q, m); // This code is contributed by patel2127 </script> |
输出:
LCA(5 4) -> 2LCA(2 3) -> 1LCA(1 3) -> 1
时间复杂性: 超线性,也就是说,几乎不比线性慢。O(N+Q)时间,其中O(N)时间用于预处理,几乎O(1)时间用于回答查询。
辅助空间: 我们使用许多数组——父数组[]、秩数组[]、祖先数组[],这些数组用于不相交的集并运算,每个数组的大小等于节点数。我们还使用了数组-child[]、sibling[]、color[],它们在这个离线算法中很有用。因此,我们使用O(N)。 为了方便起见,所有这些数组都放在一个structure-struct子集中以保存这些数组。
工具书类 https://en.wikipedia.org/wiki/Tarjan%27s_off-行\最低\公共\祖先\算法 CLRS,第21-3节,第584页,第二版/第三版 http://wcipeg.com/wiki/Lowest_common_ancestor#Offline 本文由 拉希特·贝尔瓦里亚 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以写一篇文章,然后将文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



