给定一个数字网格,找到最大长度的蛇序列并打印出来。如果存在多个长度最大的蛇序列,请打印其中任何一个。 snake序列由网格中的相邻数字组成,因此对于每个数字,右边的数字或下面的数字都是其值的+1或-1。例如,如果您位于网格中的位置(x,y),如果该数字为±1,则可以向右移动,即(x,y+1),如果该数字为±1,则可以向下移动,即(x+1,y)。 例如 9 , 6, 5, 2 8, 7, 6, 5 7, 3, 1, 6. 1, 1, 1, 7. 在上面的网格中,最长的蛇序列是:(9,8,7,6,5,6,7) 下图显示了所有可能的路径——
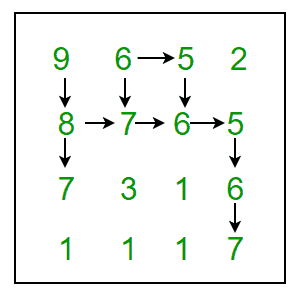
我们强烈建议您尽量减少浏览器,并先自己尝试。 其思想是使用动态规划。对于矩阵的每个单元,我们保持蛇在当前单元中的最大长度。最大长度蛇序列将具有最大值。最大值单元格将对应于蛇的尾巴。为了打印蛇,我们需要从尾巴一直回溯到蛇头。 允许 T[i][i] 表示以单元(i,j)结尾的蛇的最大长度,那么对于给定的矩阵M,DP关系定义为—— T[0][0]=0 T[i][j]=max(T[i][j],T[i][j-1]+1)如果M[i][j]=M[i][j-1]±1 T[i][j]=max(T[i][j],T[i-1][j]+1)如果M[i][j]=M[i-1][j]±1 以下是该想法的实施情况——
C++
// C++ program to find maximum length // Snake sequence and print it #include <bits/stdc++.h> using namespace std; #define M 4 #define N 4 struct Point { int x, y; }; // Function to find maximum length Snake sequence path // (i, j) corresponds to tail of the snake list<Point> findPath( int grid[M][N], int mat[M][N], int i, int j) { list<Point> path; Point pt = {i, j}; path.push_front(pt); while (grid[i][j] != 0) { if (i > 0 && grid[i][j] - 1 == grid[i - 1][j]) { pt = {i - 1, j}; path.push_front(pt); i--; } else if (j > 0 && grid[i][j] - 1 == grid[i][j - 1]) { pt = {i, j - 1}; path.push_front(pt); j--; } } return path; } // Function to find maximum length Snake sequence void findSnakeSequence( int mat[M][N]) { // table to store results of subproblems int lookup[M][N]; // initialize by 0 memset (lookup, 0, sizeof lookup); // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for ( int i = 0; i < M; i++) { for ( int j = 0; j < N; j++) { // do except for (0, 0) cell if (i || j) { // look above if (i > 0 && abs (mat[i - 1][j] - mat[i][j]) == 1) { lookup[i][j] = max(lookup[i][j], lookup[i - 1][j] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i, max_col = j; } } // look left if (j > 0 && abs (mat[i][j - 1] - mat[i][j]) == 1) { lookup[i][j] = max(lookup[i][j], lookup[i][j - 1] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i, max_col = j; } } } } } cout << "Maximum length of Snake sequence is: " << max_len << endl; // find maximum length Snake sequence path list<Point> path = findPath(lookup, mat, max_row, max_col); cout << "Snake sequence is:" ; for ( auto it = path.begin(); it != path.end(); it++) cout << endl << mat[it->x][it->y] << " (" << it->x << ", " << it->y << ")" ; } // Driver code int main() { int mat[M][N] = { {9, 6, 5, 2}, {8, 7, 6, 5}, {7, 3, 1, 6}, {1, 1, 1, 7}, }; findSnakeSequence(mat); return 0; } |
JAVA
// Java program to find maximum length // Snake sequence and print it import java.util.*; class GFG { static int M = 4 ; static int N = 4 ; static class Point { int x, y; public Point( int x, int y) { this .x = x; this .y = y; } }; // Function to find maximum length Snake sequence path // (i, j) corresponds to tail of the snake static List<Point> findPath( int grid[][], int mat[][], int i, int j) { List<Point> path = new LinkedList<>(); Point pt = new Point(i, j); path.add( 0 , pt); while (grid[i][j] != 0 ) { if (i > 0 && grid[i][j] - 1 == grid[i - 1 ][j]) { pt = new Point(i - 1 , j); path.add( 0 , pt); i--; } else if (j > 0 && grid[i][j] - 1 == grid[i][j - 1 ]) { pt = new Point(i, j - 1 ); path.add( 0 , pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence( int mat[][]) { // table to store results of subproblems int [][]lookup = new int [M][N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M; i++) { for ( int j = 0 ; j < N; j++) { // do except for (0, 0) cell if (i != 0 || j != 0 ) { // look above if (i > 0 && Math.abs(mat[i - 1 ][j] - mat[i][j]) == 1 ) { lookup[i][j] = Math.max(lookup[i][j], lookup[i - 1 ][j] + 1 ); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.abs(mat[i][j - 1 ] - mat[i][j]) == 1 ) { lookup[i][j] = Math.max(lookup[i][j], lookup[i][j - 1 ] + 1 ); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } } } } System.out.print( "Maximum length of Snake " + "sequence is: " + max_len + "" ); // find maximum length Snake sequence path List<Point> path = findPath(lookup, mat, max_row, max_col); System.out.print( "Snake sequence is:" ); for (Point it : path) System.out.print( "" + mat[it.x][it.y] + " (" + it.x + ", " + it.y + ")" ); } // Driver code public static void main(String[] args) { int mat[][] = {{ 9 , 6 , 5 , 2 }, { 8 , 7 , 6 , 5 }, { 7 , 3 , 1 , 6 }, { 1 , 1 , 1 , 7 }}; findSnakeSequence(mat); } } // This code is contributed by 29AjayKumar |
Python3]
// C# program to find maximum length// Snake sequence and print itusing System;using System.Collections.Generic; class GFG {static int M = 4;static int N = 4;public class Point{ public int x, y; public Point(int x, int y) { this.x = x; this.y = y; }};// Function to find maximum length Snake sequence path// (i, j) corresponds to tail of the snakestatic List<Point> findPath(int [,]grid, int [,]mat, int i, int j){ List<Point> path = new List<Point>(); Point pt = new Point(i, j); path.Insert(0, pt); while (grid[i, j] != 0) { if (i > 0 && grid[i, j] - 1 == grid[i - 1, j]) { pt = new Point(i - 1, j); path.Insert(0, pt); i--; } else if (j > 0 && grid[i, j] - 1 == grid[i, j - 1]) { pt = new Point(i, j - 1); path.Insert(0, pt); j--; } } return path;}// Function to find maximum length Snake sequencestatic void findSnakeSequence(int [,]mat){ // table to store results of subproblems int [,]lookup = new int[M, N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0, 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.Abs(mat[i - 1, j] - mat[i, j]) == 1) { lookup[i, j] = Math.Max(lookup[i, j], lookup[i - 1, j] + 1); if (max_len < lookup[i,j]) { max_len = lookup[i, j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.Abs(mat[i, j - 1] - mat[i, j]) == 1) { lookup[i, j] = Math.Max(lookup[i, j], lookup[i, j - 1] + 1); if (max_len < lookup[i, j]) { max_len = lookup[i, j]; max_row = i; max_col = j; } } } } } Console.Write("Maximum length of Snake " + "sequence is: " + max_len + ""); // find maximum length Snake sequence path List<Point> path = findPath(lookup, mat, max_row, max_col); Console.Write("Snake sequence is:"); foreach (Point it in path) Console.Write("" + mat[it.x,it.y] + " (" + it.x + ", " + it.y + ")");}// Driver codepublic static void Main(String[] args){ int [,]mat = {{9, 6, 5, 2}, {8, 7, 6, 5}, {7, 3, 1, 6}, {1, 1, 1, 7}}; findSnakeSequence(mat);}}// This code is contributed by Princi Singh输出:
Maximum length of Snake sequence is: 6Snake sequence is:9 (0, 0)8 (1, 0)7 (1, 1)6 (1, 2)5 (1, 3)6 (2, 3)7 (3, 3)
上述解的时间复杂度为O(M*N)。上述解决方案使用的辅助空间是O(M*N)。如果我们不需要打印snake,空间可以进一步减少到O(N),因为我们只使用最后一行的结果。 参考: 堆栈溢出 本文由 阿迪蒂亚·戈尔 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以写一篇文章,然后将文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



