网络拓扑排序 D 定向的 A. 循环的 G raph(DAG)是顶点的线性排序,因此对于每个有向边uv,顶点u在排序中位于v之前。如果图形不是DAG,则无法对其进行拓扑排序。 给定一个DAG,打印所有拓扑类型的图形。
null
For example, consider the below graph.
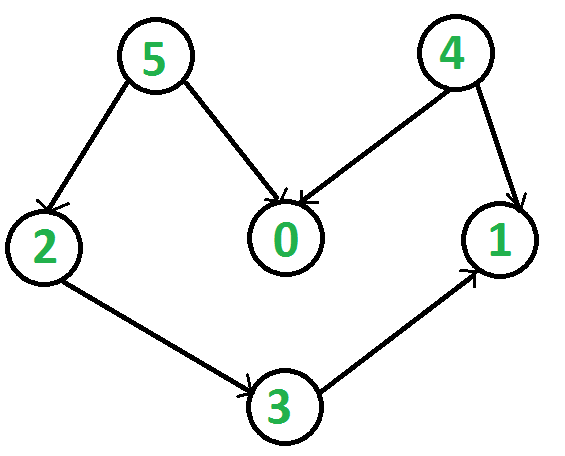
给定图形的所有拓扑类型如下: 4 5 0 2 3 1 4 5 2 0 3 1 4 5 2 3 0 1 4 5 2 3 1 0 5 2 3 4 0 1 5 2 3 4 1 0 5 2 4 0 3 1 5 2 4 3 0 1 5 2 4 3 1 0 5 4 0 2 3 1 5 4 2 0 3 1 5 4 2 3 0 1 5 4 2 3 1 0
在一个有向无环图中,很多时候我们可以有彼此无关的顶点,因为我们可以用很多方式对它们排序。这些不同的拓扑排序在很多情况下都很重要,例如,如果顶点之间也有一些相对权重,这是为了最小化,那么我们需要考虑相对排序以及它们的相对权重,这就需要检查所有可能的拓扑排序。 我们可以通过回溯完成所有可能的排序,算法步骤如下:
- 将所有顶点初始化为未访问。
- 现在选择未访问且索引为零的顶点,并将所有这些顶点的索引减少1(对应于删除边),现在将该顶点添加到结果中,再次调用递归函数并回溯。
- 从函数重置值返回访问后,返回其他可能性枚举的结果和indegree。
以下是上述步骤的实施。
C++
// C++ program to print all topological sorts of a graph #include <bits/stdc++.h> using namespace std; class Graph { int V; // No. of vertices // Pointer to an array containing adjacency list list< int > *adj; // Vector to store indegree of vertices vector< int > indegree; // A function used by alltopologicalSort void alltopologicalSortUtil(vector< int >& res, bool visited[]); public : Graph( int V); // Constructor // function to add an edge to graph void addEdge( int v, int w); // Prints all Topological Sorts void alltopologicalSort(); }; // Constructor of graph Graph::Graph( int V) { this ->V = V; adj = new list< int >[V]; // Initialising all indegree with 0 for ( int i = 0; i < V; i++) indegree.push_back(0); } // Utility function to add edge void Graph::addEdge( int v, int w) { adj[v].push_back(w); // Add w to v's list. // increasing inner degree of w by 1 indegree[w]++; } // Main recursive function to print all possible // topological sorts void Graph::alltopologicalSortUtil(vector< int >& res, bool visited[]) { // To indicate whether all topological are found // or not bool flag = false ; for ( int i = 0; i < V; i++) { // If indegree is 0 and not yet visited then // only choose that vertex if (indegree[i] == 0 && !visited[i]) { // reducing indegree of adjacent vertices list< int >:: iterator j; for (j = adj[i].begin(); j != adj[i].end(); j++) indegree[*j]--; // including in result res.push_back(i); visited[i] = true ; alltopologicalSortUtil(res, visited); // resetting visited, res and indegree for // backtracking visited[i] = false ; res.erase(res.end() - 1); for (j = adj[i].begin(); j != adj[i].end(); j++) indegree[*j]++; flag = true ; } } // We reach here if all vertices are visited. // So we print the solution here if (!flag) { for ( int i = 0; i < res.size(); i++) cout << res[i] << " " ; cout << endl; } } // The function does all Topological Sort. // It uses recursive alltopologicalSortUtil() void Graph::alltopologicalSort() { // Mark all the vertices as not visited bool *visited = new bool [V]; for ( int i = 0; i < V; i++) visited[i] = false ; vector< int > res; alltopologicalSortUtil(res, visited); } // Driver program to test above functions int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << "All Topological sorts" ; g.alltopologicalSort(); return 0; } |
JAVA
//Java program to print all topological sorts of a graph import java.util.*; class Graph { int V; // No. of vertices List<Integer> adjListArray[]; public Graph( int V) { this .V = V; @SuppressWarnings ( "unchecked" ) List<Integer> adjListArray[] = new LinkedList[V]; this .adjListArray = adjListArray; for ( int i = 0 ; i < V; i++) { adjListArray[i] = new LinkedList<>(); } } // Utility function to add edge public void addEdge( int src, int dest) { this .adjListArray[src].add(dest); } // Main recursive function to print all possible // topological sorts private void allTopologicalSortsUtil( boolean [] visited, int [] indegree, ArrayList<Integer> stack) { // To indicate whether all topological are found // or not boolean flag = false ; for ( int i = 0 ; i < this .V; i++) { // If indegree is 0 and not yet visited then // only choose that vertex if (!visited[i] && indegree[i] == 0 ) { // including in result visited[i] = true ; stack.add(i); for ( int adjacent : this .adjListArray[i]) { indegree[adjacent]--; } allTopologicalSortsUtil(visited, indegree, stack); // resetting visited, res and indegree for // backtracking visited[i] = false ; stack.remove(stack.size() - 1 ); for ( int adjacent : this .adjListArray[i]) { indegree[adjacent]++; } flag = true ; } } // We reach here if all vertices are visited. // So we print the solution here if (!flag) { stack.forEach(i -> System.out.print(i + " " )); System.out.println(); } } // The function does all Topological Sort. // It uses recursive alltopologicalSortUtil() public void allTopologicalSorts() { // Mark all the vertices as not visited boolean [] visited = new boolean [ this .V]; int [] indegree = new int [ this .V]; for ( int i = 0 ; i < this .V; i++) { for ( int var : this .adjListArray[i]) { indegree[var]++; } } ArrayList<Integer> stack = new ArrayList<>(); allTopologicalSortsUtil(visited, indegree, stack); } // Driver code public static void main(String[] args) { // Create a graph given in the above diagram Graph graph = new Graph( 6 ); graph.addEdge( 5 , 2 ); graph.addEdge( 5 , 0 ); graph.addEdge( 4 , 0 ); graph.addEdge( 4 , 1 ); graph.addEdge( 2 , 3 ); graph.addEdge( 3 , 1 ); System.out.println( "All Topological sorts" ); graph.allTopologicalSorts(); } } |
Python3
# class to represent a graph object class Graph: # Constructor def __init__( self , edges, N): # A List of Lists to represent an adjacency list self .adjList = [[] for _ in range (N)] # stores in-degree of a vertex # initialize in-degree of each vertex by 0 self .indegree = [ 0 ] * N # add edges to the undirected graph for (src, dest) in edges: # add an edge from source to destination self .adjList[src].append(dest) # increment in-degree of destination vertex by 1 self .indegree[dest] = self .indegree[dest] + 1 # Recursive function to find # all topological orderings of a given DAG def findAllTopologicalOrders(graph, path, discovered, N): # do for every vertex for v in range (N): # proceed only if in-degree of current node is 0 and # current node is not processed yet if graph.indegree[v] = = 0 and not discovered[v]: # for every adjacent vertex u of v, # reduce in-degree of u by 1 for u in graph.adjList[v]: graph.indegree[u] = graph.indegree[u] - 1 # include current node in the path # and mark it as discovered path.append(v) discovered[v] = True # recur findAllTopologicalOrders(graph, path, discovered, N) # backtrack: reset in-degree # information for the current node for u in graph.adjList[v]: graph.indegree[u] = graph.indegree[u] + 1 # backtrack: remove current node from the path and # mark it as undiscovered path.pop() discovered[v] = False # print the topological order if # all vertices are included in the path if len (path) = = N: print (path) # Print all topological orderings of a given DAG def printAllTopologicalOrders(graph): # get number of nodes in the graph N = len (graph.adjList) # create an auxiliary space to keep track of whether vertex is discovered discovered = [ False ] * N # list to store the topological order path = [] # find all topological ordering and print them findAllTopologicalOrders(graph, path, discovered, N) # Driver code if __name__ = = '__main__' : # List of graph edges as per above diagram edges = [( 5 , 2 ), ( 5 , 0 ), ( 4 , 0 ), ( 4 , 1 ), ( 2 , 3 ), ( 3 , 1 )] print ( "All Topological sorts" ) # Number of nodes in the graph N = 6 # create a graph from edges graph = Graph(edges, N) # print all topological ordering of the graph printAllTopologicalOrders(graph) # This code is contributed by Priyadarshini Kumari |
输出:
All Topological sorts4 5 0 2 3 1 4 5 2 0 3 1 4 5 2 3 0 1 4 5 2 3 1 0 5 2 3 4 0 1 5 2 3 4 1 0 5 2 4 0 3 1 5 2 4 3 0 1 5 2 4 3 1 0 5 4 0 2 3 1 5 4 2 0 3 1 5 4 2 3 0 1 5 4 2 3 1 0
本文由乌特卡什·特里维迪撰稿。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



