本文描述了一种通过将树中两个节点的LCA简化为RMQ问题来解决该问题的方法。
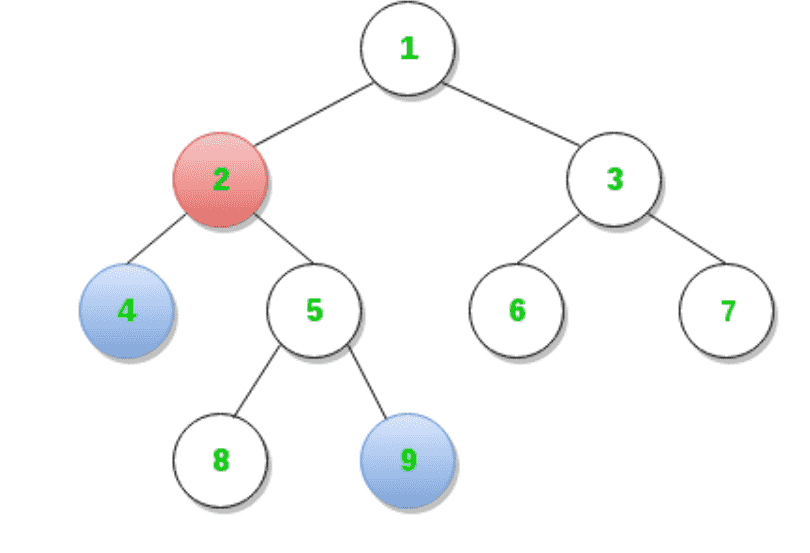
最低共同祖先(LCA) 在有根树的两个节点u和v中,T被定义为距离根最远的节点,其u和v都是子节点。 例如,在下图中,节点4和节点9的LCA是节点2。
有很多方法可以解决生命周期评价问题。这些方法的时间和空间复杂性各不相同。 在这里 是其中几个的链接(这些不涉及降低RMQ)。
范围最小查询(RMQ) 在数组上使用,以查找两个指定索引之间具有最小值的元素的位置。讨论了解决RMQ的不同方法 在这里 和 在这里 本文讨论了基于分段树的方法。对于段树,预处理时间为O(n),最小查询范围的时间为O(Logn)。存储段树所需的额外空间为O(n)。
将LCA降低至RMQ: 其思想是通过一个Euler遍历(不使用提升铅笔的遍历)从根开始遍历树,这是一种DFS类型的遍历,具有前序遍历特性。
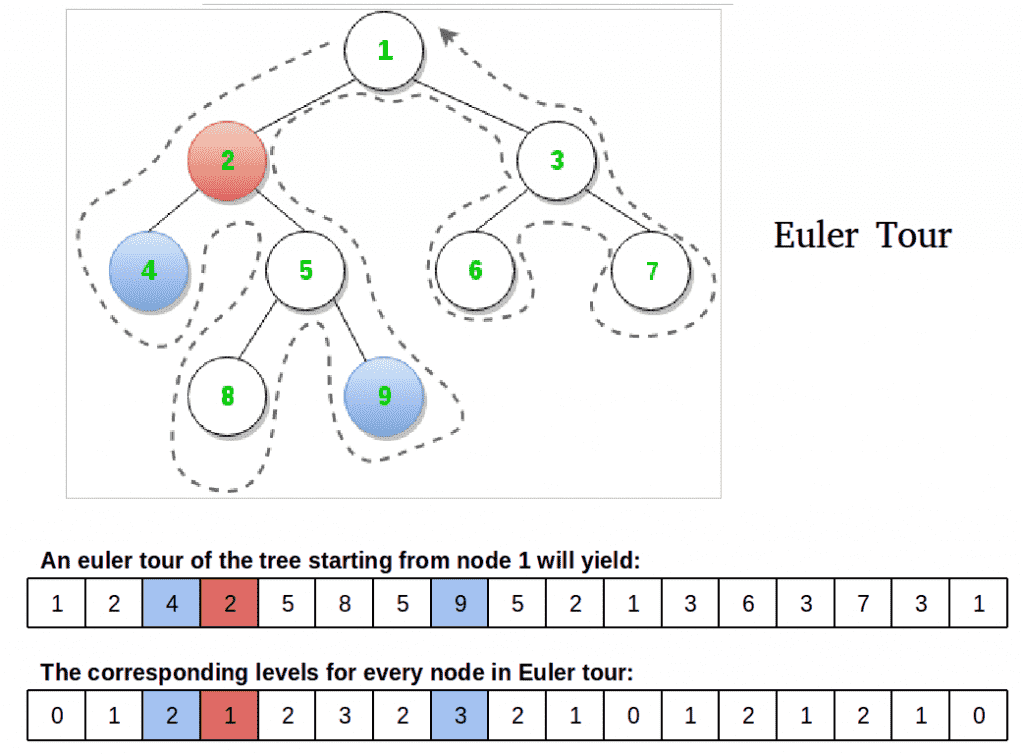
观察 :节点4和9的LCA是节点2,在T的DFS期间,在4和9的访问之间遇到的所有节点中,节点2恰好是最靠近根的节点。该观察是减少的关键。让我们换一种说法:我们的节点是最小级别的节点,也是T的Euler tour中u和v连续出现(任意)之间的所有节点中该级别的唯一节点。 我们需要三个阵列来实现:
- 按T的Euler巡回顺序访问的节点
- 在T的Euler tour中访问的每个节点的级别
- 索引 第一 在T的Euler旅行中出现一个节点(因为任何出现都是好的,所以让我们跟踪第一个)

算法:
- 在树上执行Euler漫游,并填充Euler、level和first Occession数组。
- 使用第一次出现的数组,获得与两个节点对应的索引,这两个节点将是水平数组中的范围角,该数组被馈送到RMQ算法以获得最小值。
- 一旦算法返回范围内最小级别的索引,我们使用它来确定使用Euler tour数组的LCA。
下面是上述算法的实现。
C++
/* C++ Program to find LCA of u and v by reducing the problem to RMQ */ #include<bits/stdc++.h> #define V 9 // number of nodes in input tree int euler[2*V - 1]; // For Euler tour sequence int level[2*V - 1]; // Level of nodes in tour sequence int firstOccurrence[V+1]; // First occurrences of nodes in tour int ind; // Variable to fill-in euler and level arrays // A Binary Tree node struct Node { int key; struct Node *left, *right; }; // Utility function creates a new binary tree node with given key Node * newNode( int k) { Node *temp = new Node; temp->key = k; temp->left = temp->right = NULL; return temp; } // log base 2 of x int Log2( int x) { int ans = 0 ; while (x>>=1) ans++; return ans ; } /* A recursive function to get the minimum value in a given range of array indexes. The following are parameters for this function. st --> Pointer to segment tree index --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0 ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[index] qs & qe --> Starting and ending indexes of query range */ int RMQUtil( int index, int ss, int se, int qs, int qe, int *st) { // If segment of this node is a part of given range, then return // the min of the segment if (qs <= ss && qe >= se) return st[index]; // If segment of this node is outside the given range else if (se < qs || ss > qe) return -1; // If a part of this segment overlaps with the given range int mid = (ss + se)/2; int q1 = RMQUtil(2*index+1, ss, mid, qs, qe, st); int q2 = RMQUtil(2*index+2, mid+1, se, qs, qe, st); if (q1==-1) return q2; else if (q2==-1) return q1; return (level[q1] < level[q2]) ? q1 : q2; } // Return minimum of elements in range from index qs (query start) to // qe (query end). It mainly uses RMQUtil() int RMQ( int *st, int n, int qs, int qe) { // Check for erroneous input values if (qs < 0 || qe > n-1 || qs > qe) { printf ( "Invalid Input" ); return -1; } return RMQUtil(0, 0, n-1, qs, qe, st); } // A recursive function that constructs Segment Tree for array[ss..se]. // si is index of current node in segment tree st void constructSTUtil( int si, int ss, int se, int arr[], int *st) { // If there is one element in array, store it in current node of // segment tree and return if (ss == se)st[si] = ss; else { // If there are more than one elements, then recur for left and // right subtrees and store the minimum of two values in this node int mid = (ss + se)/2; constructSTUtil(si*2+1, ss, mid, arr, st); constructSTUtil(si*2+2, mid+1, se, arr, st); if (arr[st[2*si+1]] < arr[st[2*si+2]]) st[si] = st[2*si+1]; else st[si] = st[2*si+2]; } } /* Function to construct segment tree from given array. This function allocates memory for segment tree and calls constructSTUtil() to fill the allocated memory */ int *constructST( int arr[], int n) { // Allocate memory for segment tree // Height of segment tree int x = Log2(n)+1; // Maximum size of segment tree int max_size = 2*(1<<x) - 1; // 2*pow(2,x) -1 int *st = new int [max_size]; // Fill the allocated memory st constructSTUtil(0, 0, n-1, arr, st); // Return the constructed segment tree return st; } // Recursive version of the Euler tour of T void eulerTour(Node *root, int l) { /* if the passed node exists */ if (root) { euler[ind] = root->key; // insert in euler array level[ind] = l; // insert l in level array ind++; // increment index /* if unvisited, mark first occurrence */ if (firstOccurrence[root->key] == -1) firstOccurrence[root->key] = ind-1; /* tour left subtree if exists, and remark euler and level arrays for parent on return */ if (root->left) { eulerTour(root->left, l+1); euler[ind]=root->key; level[ind] = l; ind++; } /* tour right subtree if exists, and remark euler and level arrays for parent on return */ if (root->right) { eulerTour(root->right, l+1); euler[ind]=root->key; level[ind] = l; ind++; } } } // Returns LCA of nodes n1, n2 (assuming they are // present in the tree) int findLCA(Node *root, int u, int v) { /* Mark all nodes unvisited. Note that the size of firstOccurrence is 1 as node values which vary from 1 to 9 are used as indexes */ memset (firstOccurrence, -1, sizeof ( int )*(V+1)); /* To start filling euler and level arrays from index 0 */ ind = 0; /* Start Euler tour with root node on level 0 */ eulerTour(root, 0); /* construct segment tree on level array */ int *st = constructST(level, 2*V-1); /* If v before u in Euler tour. For RMQ to work, first parameter 'u' must be smaller than second 'v' */ if (firstOccurrence[u]>firstOccurrence[v]) std::swap(u, v); // Starting and ending indexes of query range int qs = firstOccurrence[u]; int qe = firstOccurrence[v]; // query for index of LCA in tour int index = RMQ(st, 2*V-1, qs, qe); /* return LCA node */ return euler[index]; } // Driver program to test above functions int main() { // Let us create the Binary Tree as shown in the diagram. Node * root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); root->right->left = newNode(6); root->right->right = newNode(7); root->left->right->left = newNode(8); root->left->right->right = newNode(9); int u = 4, v = 9; printf ( "The LCA of node %d and node %d is node %d." , u, v, findLCA(root, u, v)); return 0; } |
JAVA
// Java program to find LCA of u and v by reducing problem to RMQ import java.util.*; // A binary tree node class Node { Node left, right; int data; Node( int item) { data = item; left = right = null ; } } class St_class { int st; int stt[] = new int [ 10000 ]; } class BinaryTree { Node root; int v = 9 ; // v is the highest value of node in our tree int euler[] = new int [ 2 * v - 1 ]; // for euler tour sequence int level[] = new int [ 2 * v - 1 ]; // level of nodes in tour sequence int f_occur[] = new int [ 2 * v - 1 ]; // to store 1st occurrence of nodes int fill; // variable to fill euler and level arrays St_class sc = new St_class(); // log base 2 of x int Log2( int x) { int ans = 0 ; int y = x >>= 1 ; while (y-- != 0 ) ans++; return ans; } int swap( int a, int b) { return a; } /* A recursive function to get the minimum value in a given range of array indexes. The following are parameters for this function. st --> Pointer to segment tree index --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0 ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[index] qs & qe --> Starting and ending indexes of query range */ int RMQUtil( int index, int ss, int se, int qs, int qe, St_class st) { // If segment of this node is a part of given range, then return // the min of the segment if (qs <= ss && qe >= se) return st.stt[index]; // If segment of this node is outside the given range else if (se < qs || ss > qe) return - 1 ; // If a part of this segment overlaps with the given range int mid = (ss + se) / 2 ; int q1 = RMQUtil( 2 * index + 1 , ss, mid, qs, qe, st); int q2 = RMQUtil( 2 * index + 2 , mid + 1 , se, qs, qe, st); if (q1 == - 1 ) return q2; else if (q2 == - 1 ) return q1; return (level[q1] < level[q2]) ? q1 : q2; } // Return minimum of elements in range from index qs (query start) to // qe (query end). It mainly uses RMQUtil() int RMQ(St_class st, int n, int qs, int qe) { // Check for erroneous input values if (qs < 0 || qe > n - 1 || qs > qe) { System.out.println( "Invalid input" ); return - 1 ; } return RMQUtil( 0 , 0 , n - 1 , qs, qe, st); } // A recursive function that constructs Segment Tree for array[ss..se]. // si is index of current node in segment tree st void constructSTUtil( int si, int ss, int se, int arr[], St_class st) { // If there is one element in array, store it in current node of // segment tree and return if (ss == se) st.stt[si] = ss; else { // If there are more than one elements, then recur for left and // right subtrees and store the minimum of two values in this node int mid = (ss + se) / 2 ; constructSTUtil(si * 2 + 1 , ss, mid, arr, st); constructSTUtil(si * 2 + 2 , mid + 1 , se, arr, st); if (arr[st.stt[ 2 * si + 1 ]] < arr[st.stt[ 2 * si + 2 ]]) st.stt[si] = st.stt[ 2 * si + 1 ]; else st.stt[si] = st.stt[ 2 * si + 2 ]; } } /* Function to construct segment tree from given array. This function allocates memory for segment tree and calls constructSTUtil() to fill the allocated memory */ int constructST( int arr[], int n) { // Allocate memory for segment tree // Height of segment tree int x = Log2(n) + 1 ; // Maximum size of segment tree int max_size = 2 * ( 1 << x) - 1 ; // 2*pow(2,x) -1 sc.stt = new int [max_size]; // Fill the allocated memory st constructSTUtil( 0 , 0 , n - 1 , arr, sc); // Return the constructed segment tree return sc.st; } // Recursive version of the Euler tour of T void eulerTour(Node node, int l) { /* if the passed node exists */ if (node != null ) { euler[fill] = node.data; // insert in euler array level[fill] = l; // insert l in level array fill++; // increment index /* if unvisited, mark first occurrence */ if (f_occur[node.data] == - 1 ) f_occur[node.data] = fill - 1 ; /* tour left subtree if exists, and remark euler and level arrays for parent on return */ if (node.left != null ) { eulerTour(node.left, l + 1 ); euler[fill] = node.data; level[fill] = l; fill++; } /* tour right subtree if exists, and remark euler and level arrays for parent on return */ if (node.right != null ) { eulerTour(node.right, l + 1 ); euler[fill] = node.data; level[fill] = l; fill++; } } } // returns LCA of node n1 and n2 assuming they are present in tree int findLCA(Node node, int u, int v) { /* Mark all nodes unvisited. Note that the size of firstOccurrence is 1 as node values which vary from 1 to 9 are used as indexes */ Arrays.fill(f_occur, - 1 ); /* To start filling euler and level arrays from index 0 */ fill = 0 ; /* Start Euler tour with root node on level 0 */ eulerTour(root, 0 ); /* construct segment tree on level array */ sc.st = constructST(level, 2 * v - 1 ); /* If v before u in Euler tour. For RMQ to work, first parameter 'u' must be smaller than second 'v' */ if (f_occur[u] > f_occur[v]) u = swap(u, u = v); // Starting and ending indexes of query range int qs = f_occur[u]; int qe = f_occur[v]; // query for index of LCA in tour int index = RMQ(sc, 2 * v - 1 , qs, qe); /* return LCA node */ return euler[index]; } // Driver program to test above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); // Let us create the Binary Tree as shown in the diagram. tree.root = new Node( 1 ); tree.root.left = new Node( 2 ); tree.root.right = new Node( 3 ); tree.root.left.left = new Node( 4 ); tree.root.left.right = new Node( 5 ); tree.root.right.left = new Node( 6 ); tree.root.right.right = new Node( 7 ); tree.root.left.right.left = new Node( 8 ); tree.root.left.right.right = new Node( 9 ); int u = 4 , v = 9 ; System.out.println( "The LCA of node " + u + " and " + v + " is " + tree.findLCA(tree.root, u, v)); } } // This code has been contributed by Mayank Jaiswal |
Python3
# Python3 program to find LCA of u and v by # reducing the problem to RMQ from math import log2, floor from typing import List class Node: def __init__( self , val: int ): self .val, self .left, self .right = val, None , None class BinaryTree: def __init__( self , root: Node): self .root = root self .val_max = self ._get_max_val() self .euler = [ 0 ] * ( 2 * self .val_max - 1 ) self .level = [ 0 ] * ( 2 * self .val_max - 1 ) self .f_occur = [ - 1 ] * ( self .val_max + 1 ) self .fill = 0 self .segment_tree = [] def _get_max_val( self ): stack = [ self .root] max_val = - 1 while stack: x = stack.pop() if x.val > max_val: max_val = x.val if x.left: stack.append(x.left) if x.right: stack.append(x.right) return max_val ''' A recursive function to get the minimum value in a given range of array indexes. The following are parameters for this function. st --> Pointer to segment tree index --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0 ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[index] qs & qe --> Starting and ending indexes of query range ''' def rmq_util( self , index, ss, se, qs, qe) - > int : # If segment of this node is part of given range # then return the min of the segment if qs < = ss and qe > = se: return self .segment_tree[index] # If segment of this node is outside # the given range elif se < qs or ss > qe: return - 1 # If part of this segment overlaps with # given range mid = (ss + se) / / 2 q1 = self .rmq_util( 2 * index + 1 , ss, mid, qs, qe) q2 = self .rmq_util( 2 * index + 2 , mid + 1 , se, qs, qe) if q1 = = - 1 : return q2 if q2 = = - 1 : return q1 return (q1 if self .level[q1] < self .level[q2] else q2) # Return minimum of elements in range from # index qs (query start) to qe (query end). # It mainly uses rmq_util() def rmq( self , n: int , qs: int , qe: int ) - > int : if qs < 0 or qe > n - 1 or qs > qe: print ( 'invalid input' ) return - 1 return self .rmq_util( 0 , 0 , n - 1 , qs, qe) # A recursive function that constructs Segment # Tree for array[ss..se]. si is index of # current node in segment tree st def construct_segment_tree_util( self , si, ss, se, arr): # If there is one element in array, # store it in current node of segment tree # and return if ss = = se: self .segment_tree[si] = ss else : # If there are more than one elements, # then recur for left and right subtrees and # store the min of two values in this node mid = (ss + se) / / 2 index_left, index_right = si * 2 + 1 , si * 2 + 2 self .construct_segment_tree_util( index_left, ss, mid, arr) self .construct_segment_tree_util( index_right, mid + 1 , se, arr) if (arr[ self .segment_tree[index_left]] < arr[ self .segment_tree[index_right]]): self .segment_tree[si] = self .segment_tree[index_left] else : self .segment_tree[si] = self .segment_tree[index_right] # Function to construct segment tree from given # array. This function allocates memory for segment # tree and calls construct_segment_tree_util() # to fill the allocated memory def construct_segment_tree( self , arr: List , n: int ): # Height of segment tree x = floor(log2(n) + 1 ) # Maximum size of segment tree max_size = 2 * ( 1 << x) - 1 # 2*pow(2,x) -1 self .segment_tree = [ 0 ] * max_size # Fill the allocated memory st self .construct_segment_tree_util( 0 , 0 , n - 1 , arr) # Recursive version of the Euler tour of T def euler_tour( self , node: Node, lev: int ): # If the passed node exists if node is not None : self .euler[ self .fill] = node.val self .level[ self .fill] = lev self .fill + = 1 # If unvisited, mark first occurence if self .f_occur[node.val] = = - 1 : self .f_occur[node.val] = self .fill - 1 # Tour left subtree if exists and remark # euler and level arrays for parent on # return if node.left is not None : self .euler_tour(node.left, lev + 1 ) self .euler[ self .fill] = node.val self .level[ self .fill] = lev self .fill + = 1 # Tour right subtree if exists and # remark euler and level arrays for # parent on return if node.right is not None : self .euler_tour(node.right, lev + 1 ) self .euler[ self .fill] = node.val self .level[ self .fill] = lev self .fill + = 1 # Returns LCA of nodes n1, n2 (assuming they are # present in the tree) def find_lca( self , u: int , v: int ): # Start euler tour with root node on level 0 self .euler_tour( self .root, 0 ) # Construct segment tree on level array self .construct_segment_tree( self .level, 2 * self .val_max - 1 ) # For rmq to work, u must be smaller than v if self .f_occur[u] > self .f_occur[v]: u, v = v, u # Start and end of query range qs = self .f_occur[u] qe = self .f_occur[v] # Query for index of lca in tour index = self .rmq( 2 * self .val_max - 1 , qs, qe) # Return lca node return self .euler[index] # Driver code if __name__ = = "__main__" : root = Node( 1 ) root.left = Node( 2 ) root.right = Node( 3 ) root.left.left = Node( 4 ) root.left.right = Node( 5 ) root.right.left = Node( 6 ) root.right.right = Node( 7 ) root.left.right.left = Node( 8 ) root.left.right.right = Node( 9 ) tree = BinaryTree(root) u, v = 4 , 9 print ( 'The lca of node {} and {} is node {}' . format ( u, v, tree.find_lca(u, v))) # This code is contributed by Rajat Srivastava |
C#
// C# program to find LCA of u and // v by reducing problem to RMQ using System; // A binary tree node class Node { public Node left, right; public int data; public Node( int item) { data = item; left = right = null ; } } class St_class { public int st; public int []stt = new int [10000]; } public class BinaryTree { Node root; static int v = 9; // v is the highest value of node in our tree int []euler = new int [2 * v - 1]; // for euler tour sequence int []level = new int [2 * v - 1]; // level of nodes in tour sequence int []f_occur = new int [2 * v - 1]; // to store 1st occurrence of nodes int fill; // variable to fill euler and level arrays St_class sc = new St_class(); // log base 2 of x int Log2( int x) { int ans = 0; int y = x >>= 1; while (y-- != 0) ans++; return ans; } int swap( int a, int b) { return a; } /* A recursive function to get the minimum value in a given range of array indexes. The following are parameters for this function. st --> Pointer to segment tree index --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0 ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[index] qs & qe --> Starting and ending indexes of query range */ int RMQUtil( int index, int ss, int se, int qs, int qe, St_class st) { // If segment of this node is a part // of given range, then return // the min of the segment if (qs <= ss && qe >= se) return st.stt[index]; // If segment of this node is // outside the given range else if (se < qs || ss > qe) return -1; // If a part of this segment // overlaps with the given range int mid = (ss + se) / 2; int q1 = RMQUtil(2 * index + 1, ss, mid, qs, qe, st); int q2 = RMQUtil(2 * index + 2, mid + 1, se, qs, qe, st); if (q1 == -1) return q2; else if (q2 == -1) return q1; return (level[q1] < level[q2]) ? q1 : q2; } // Return minimum of elements in // range from index qs (query start) to // qe (query end). It mainly uses RMQUtil() int RMQ(St_class st, int n, int qs, int qe) { // Check for erroneous input values if (qs < 0 || qe > n - 1 || qs > qe) { Console.WriteLine( "Invalid input" ); return -1; } return RMQUtil(0, 0, n - 1, qs, qe, st); } // A recursive function that constructs // Segment Tree for array[ss..se]. // si is index of current node in segment tree st void constructSTUtil( int si, int ss, int se, int []arr, St_class st) { // If there is one element in array, // store it in current node of // segment tree and return if (ss == se) st.stt[si] = ss; else { // If there are more than one elements, // then recur for left and right subtrees // and store the minimum of two values in this node int mid = (ss + se) / 2; constructSTUtil(si * 2 + 1, ss, mid, arr, st); constructSTUtil(si * 2 + 2, mid + 1, se, arr, st); if (arr[st.stt[2 * si + 1]] < arr[st.stt[2 * si + 2]]) st.stt[si] = st.stt[2 * si + 1]; else st.stt[si] = st.stt[2 * si + 2]; } } /* Function to construct segment tree from given array. This function allocates memory for segment tree and calls constructSTUtil() to fill the allocated memory */ int constructST( int []arr, int n) { // Allocate memory for segment tree // Height of segment tree int x = Log2(n) + 1; // Maximum size of segment tree int max_size = 2 * (1 << x) - 1; // 2*pow(2,x) -1 sc.stt = new int [max_size]; // Fill the allocated memory st constructSTUtil(0, 0, n - 1, arr, sc); // Return the constructed segment tree return sc.st; } // Recursive version of the Euler tour of T void eulerTour(Node node, int l) { /* if the passed node exists */ if (node != null ) { euler[fill] = node.data; // insert in euler array level[fill] = l; // insert l in level array fill++; // increment index /* if unvisited, mark first occurrence */ if (f_occur[node.data] == -1) f_occur[node.data] = fill - 1; /* tour left subtree if exists, and remark euler and level arrays for parent on return */ if (node.left != null ) { eulerTour(node.left, l + 1); euler[fill] = node.data; level[fill] = l; fill++; } /* tour right subtree if exists, and remark euler and level arrays for parent on return */ if (node.right != null ) { eulerTour(node.right, l + 1); euler[fill] = node.data; level[fill] = l; fill++; } } } // returns LCA of node n1 and n2 // assuming they are present in tree int findLCA(Node node, int u, int v) { /* Mark all nodes unvisited. Note that the size of firstOccurrence is 1 as node values which vary from 1 to 9 are used as indexes */ //Arrays.fill(f_occur, -1); for ( int i = 0; i < f_occur.Length; i++) f_occur[i] = -1; /* To start filling euler and level arrays from index 0 */ fill = 0; /* Start Euler tour with root node on level 0 */ eulerTour(root, 0); /* construct segment tree on level array */ sc.st = constructST(level, 2 * v - 1); /* If v before u in Euler tour. For RMQ to work, first parameter 'u' must be smaller than second 'v' */ if (f_occur[u] > f_occur[v]) u = swap(u, u = v); // Starting and ending indexes of query range int qs = f_occur[u]; int qe = f_occur[v]; // query for index of LCA in tour int index = RMQ(sc, 2 * v - 1, qs, qe); /* return LCA node */ return euler[index]; } // Driver program to test above functions public static void Main(String []args) { BinaryTree tree = new BinaryTree(); // Let us create the Binary Tree // as shown in the diagram. tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); tree.root.right.left = new Node(6); tree.root.right.right = new Node(7); tree.root.left.right.left = new Node(8); tree.root.left.right.right = new Node(9); int u = 4, v = 9; Console.WriteLine( "The LCA of node " + u + " and " + v + " is " + tree.findLCA(tree.root, u, v)); } } // This code is contributed by 29AjayKumar |
Javascript
<script> // JavaScript program to find LCA of u and v // by reducing problem to RMQ // A binary tree node class Node { constructor(item) { this .data=item; this .left = this .right = null ; } } class St_class { st; stt= new Array(10000); } let root; // v is the highest value of node in our tree let v = 9; // for euler tour sequence let euler = new Array(2 * v - 1); // level of nodes in tour sequence let level = new Array(2 * v - 1); // to store 1st occurrence of nodes let f_occur = new Array(2 * v - 1); let fill; // variable to fill euler and level arrays let sc = new St_class(); // log base 2 of x function Log2(x) { let ans = 0; let y = x >>= 1; while (y-- != 0) ans++; return ans; } function swap(a,b) { return a; } /* A recursive function to get the minimum value in a given range of array indexes. The following are parameters for this function. st --> Pointer to segment tree index --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0 ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[index] qs & qe --> Starting and ending indexes of query range */ function RMQUtil(index,ss,se,qs,qe,st) { // If segment of this node is a part // of given range, then return // the min of the segment if (qs <= ss && qe >= se) return st.stt[index]; // If segment of this node is // outside the given range else if (se < qs || ss > qe) return -1; // If a part of this segment overlaps // with the given range let mid = Math.floor((ss + se) / 2); let q1 = RMQUtil(2 * index + 1, ss, mid, qs, qe, st); let q2 = RMQUtil(2 * index + 2, mid + 1, se, qs, qe, st); if (q1 == -1) return q2; else if (q2 == -1) return q1; return (level[q1] < level[q2]) ? q1 : q2; } // Return minimum of elements in range // from index qs (query start) to // qe (query end). It mainly uses RMQUtil() function RMQ(st,n,qs,qe) { // Check for erroneous input values if (qs < 0 || qe > n - 1 || qs > qe) { document.write( "Invalid input" ); return -1; } return RMQUtil(0, 0, n - 1, qs, qe, st); } // A recursive function that constructs // Segment Tree for array[ss..se]. // si is index of current node in segment tree st function constructSTUtil(si,ss,se,arr,st) { // If there is one element in array, // store it in current node of // segment tree and return if (ss == se) st.stt[si] = ss; else { // If there are more than one elements, // then recur for left and // right subtrees and store the minimum // of two values in this node let mid = Math.floor((ss + se) / 2); constructSTUtil(si * 2 + 1, ss, mid, arr, st); constructSTUtil(si * 2 + 2, mid + 1, se, arr, st); if (arr[st.stt[2 * si + 1]] < arr[st.stt[2 * si + 2]]) st.stt[si] = st.stt[2 * si + 1]; else st.stt[si] = st.stt[2 * si + 2]; } } /* Function to construct segment tree from given array. This function allocates memory for segment tree and calls constructSTUtil() to fill the allocated memory */ function constructST(arr,n) { // Allocate memory for segment tree // Height of segment tree let x = Log2(n) + 1; // Maximum size of segment tree let max_size = 2 * (1 << x) - 1; // 2*pow(2,x) -1 sc.stt = new Array(max_size); // Fill the allocated memory st constructSTUtil(0, 0, n - 1, arr, sc); // Return the constructed segment tree return sc.st; } // Recursive version of the Euler tour of T function eulerTour(node,l) { /* if the passed node exists */ if (node != null ) { euler[fill] = node.data; // insert in euler array level[fill] = l; // insert l in level array fill++; // increment index /* if unvisited, mark first occurrence */ if (f_occur[node.data] == -1) f_occur[node.data] = fill - 1; /* tour left subtree if exists, and remark euler and level arrays for parent on return */ if (node.left != null ) { eulerTour(node.left, l + 1); euler[fill] = node.data; level[fill] = l; fill++; } /* tour right subtree if exists, and remark euler and level arrays for parent on return */ if (node.right != null ) { eulerTour(node.right, l + 1); euler[fill] = node.data; level[fill] = l; fill++; } } } // returns LCA of node n1 and n2 // assuming they are present in tree function findLCA(node,u,v) { /* Mark all nodes unvisited. Note that the size of firstOccurrence is 1 as node values which vary from 1 to 9 are used as indexes */ for (let i=0;i<f_occur.length;i++) { f_occur[i]=-1; } /* To start filling euler and level arrays from index 0 */ fill = 0; /* Start Euler tour with root node on level 0 */ eulerTour(root, 0); /* construct segment tree on level array */ sc.st = constructST(level, 2 * v - 1); /* If v before u in Euler tour. For RMQ to work, first parameter 'u' must be smaller than second 'v' */ if (f_occur[u] > f_occur[v]) u = swap(u, u = v); // Starting and ending indexes of query range let qs = f_occur[u]; let qe = f_occur[v]; // query for index of LCA in tour let index = RMQ(sc, 2 * v - 1, qs, qe); /* return LCA node */ return euler[index]; } // Driver program to test above functions // Let us create the Binary Tree as shown in the diagram. root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7); root.left.right.left = new Node(8); root.left.right.right = new Node(9); u = 4, v = 9; document.write( "The LCA of node " + u + " and node " + v + " is node " + findLCA(root, u, v)); // This code is contributed by rag2127 </script> |
输出:
The LCA of node 4 and node 9 is node 2.
注:
- 我们假设查询的节点存在于树中。
- 我们还假设,若树中有V个节点,那个么这些节点的键(或数据)在1到V的范围内。
时间复杂性:
- Euler tour:节点数为V。对于树,E=V-1。欧拉之旅(DFS)将采用O(V+E),也就是O(2*V),可以写成O(V)。
- 分段树构造:O(n),其中n=V+E=2*V–1。
- 范围最小查询:O(日志(n))
总的来说,这种方法需要O(n)时间进行预处理,但需要O(logn)时间进行查询。因此,当我们想要在一棵树上执行大量LCA查询时,它可能很有用(请注意,LCA有助于在二叉树的两个节点之间找到最短路径)
辅助空间:
- 欧拉巡更阵列:O(n),其中n=2*V–1
- 节点级别数组:O(n)
- 首次出现数组:O(V)
- 段树:O(n)
总体:O(n) 另一个观察结果是,水平阵列中的相邻元素相差1。这可用于将RMQ问题转换为LCA问题。 本文由 亚什·瓦里亚尼 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



