斐波那契编码 使用数字的斐波那契表示法将整数编码为二进制数。这个想法是基于 泽肯多夫定理 它表示每个正整数可以唯一地写为不同的非相邻斐波那契数(0,1,1,2,3,5,8,13,21,34,55,89,144,…)之和。
特定整数的斐波那契码字正是该整数的 泽肯多夫表象 其数字顺序颠倒,并在末尾附加一个“1”。附加1表示代码结束(请注意,根据 泽肯多夫定理 表示法使用从1开始的斐波那契数(第二斐波那契数)。所以使用的斐波那契数是1,2,3,5,8,13,21,34,55,89,141……。
给定一个数字n,打印它的斐波那契码。
例如:
Input: n = 1Output: 111 is first Fibonacci number in this representationand an extra 1 is appended at the end.Input: n = 11Output: 00101111 is sum of 8 and 3. The last 1 represents extra 1that is always added. A 1 before it represents 8. Thethird 1 (from beginning) represents 3.
我们强烈建议您尽量减少浏览器,并先自己尝试。 以下算法将整数作为输入,并生成存储斐波那契编码的字符串。 找出小于或等于n的最大斐波那契数f。假设它是斐波那契数列中的第i个数。n的码字长度将为i+3个字符(一个用于结尾追加的额外1,一个用于索引,一个用于“”)。假设存储了斐波那契级数:
- 设f是小于或等于n的最大斐波那契数,在二进制字符串中加上“1”。这表示在表示n时使用f。从n中减去f:n=n–f
- 否则,如果f大于n,则在二进制字符串前加上“0”。
- 移到比f小的斐波那契数。
- 重复,直到余数为零(n=0)
- 在二进制字符串中附加一个“1”。我们得到一种编码,使得两个连续的1表示一个数字的结束(和下一个数字的开始)。
下面是上述算法的实现。
C++
/* C++ program for Fibonacci Encoding of a positive integer n */ #include <bits/stdc++.h> using namespace std; // To limit on the largest Fibonacci number to be used #define N 30 /* Array to store fibonacci numbers. fib[i] is going to store (i+2)'th Fibonacci number*/ int fib[N]; // Stores values in fib and returns index of the largest // fibonacci number smaller than n. int largestFiboLessOrEqual( int n) { fib[0] = 1; // Fib[0] stores 2nd Fibonacci No. fib[1] = 2; // Fib[1] stores 3rd Fibonacci No. // Keep Generating remaining numbers while previously // generated number is smaller int i; for (i=2; fib[i-1]<=n; i++) fib[i] = fib[i-1] + fib[i-2]; // Return index of the largest fibonacci number // smaller than or equal to n. Note that the above // loop stopped when fib[i-1] became larger. return (i-2); } /* Returns pointer to the char string which corresponds to code for n */ char * fibonacciEncoding( int n) { int index = largestFiboLessOrEqual(n); //allocate memory for codeword char *codeword = ( char *) malloc ( sizeof ( char )*(index+3)); // index of the largest Fibonacci f <= n int i = index; while (n) { // Mark usage of Fibonacci f (1 bit) codeword[i] = '1' ; // Subtract f from n n = n - fib[i]; // Move to Fibonacci just smaller than f i = i - 1; // Mark all Fibonacci > n as not used (0 bit), // progress backwards while (i>=0 && fib[i]>n) { codeword[i] = '0' ; i = i - 1; } } //additional '1' bit codeword[index+1] = '1' ; codeword[index+2] = ' ' ; //return pointer to codeword return codeword; } /* driver function */ int main() { int n = 143; cout << "Fibonacci code word for " <<n << " is " << fibonacciEncoding(n); return 0; } // This code is contributed by shivanisinghss2110 |
C
/* C program for Fibonacci Encoding of a positive integer n */ #include<stdio.h> #include<stdlib.h> // To limit on the largest Fibonacci number to be used #define N 30 /* Array to store fibonacci numbers. fib[i] is going to store (i+2)'th Fibonacci number*/ int fib[N]; // Stores values in fib and returns index of the largest // fibonacci number smaller than n. int largestFiboLessOrEqual( int n) { fib[0] = 1; // Fib[0] stores 2nd Fibonacci No. fib[1] = 2; // Fib[1] stores 3rd Fibonacci No. // Keep Generating remaining numbers while previously // generated number is smaller int i; for (i=2; fib[i-1]<=n; i++) fib[i] = fib[i-1] + fib[i-2]; // Return index of the largest fibonacci number // smaller than or equal to n. Note that the above // loop stopped when fib[i-1] became larger. return (i-2); } /* Returns pointer to the char string which corresponds to code for n */ char * fibonacciEncoding( int n) { int index = largestFiboLessOrEqual(n); //allocate memory for codeword char *codeword = ( char *) malloc ( sizeof ( char )*(index+3)); // index of the largest Fibonacci f <= n int i = index; while (n) { // Mark usage of Fibonacci f (1 bit) codeword[i] = '1' ; // Subtract f from n n = n - fib[i]; // Move to Fibonacci just smaller than f i = i - 1; // Mark all Fibonacci > n as not used (0 bit), // progress backwards while (i>=0 && fib[i]>n) { codeword[i] = '0' ; i = i - 1; } } //additional '1' bit codeword[index+1] = '1' ; codeword[index+2] = ' ' ; //return pointer to codeword return codeword; } /* driver function */ int main() { int n = 143; printf ( "Fibonacci code word for %d is %s" , n, fibonacciEncoding(n)); return 0; } |
JAVA
// Java program for Fibonacci Encoding // of a positive integer n import java.io.*; class GFG{ // To limit on the largest Fibonacci // number to be used public static int N = 30 ; // Array to store fibonacci numbers. // fib[i] is going to store (i+2)'th // Fibonacci number public static int [] fib = new int [N]; // Stores values in fib and returns index of // the largest fibonacci number smaller than n. public static int largestFiboLessOrEqual( int n) { // Fib[0] stores 2nd Fibonacci No. fib[ 0 ] = 1 ; // Fib[1] stores 3rd Fibonacci No. fib[ 1 ] = 2 ; // Keep Generating remaining numbers while // previously generated number is smaller int i; for (i = 2 ; fib[i - 1 ] <= n; i++) { fib[i] = fib[i - 1 ] + fib[i - 2 ]; } // Return index of the largest fibonacci // number smaller than or equal to n. // Note that the above loop stopped when // fib[i-1] became larger. return (i - 2 ); } // Returns pointer to the char string which // corresponds to code for n public static String fibonacciEncoding( int n) { int index = largestFiboLessOrEqual(n); // Allocate memory for codeword char [] codeword = new char [index + 3 ]; // Index of the largest Fibonacci f <= n int i = index; while (n > 0 ) { // Mark usage of Fibonacci f(1 bit) codeword[i] = '1' ; // Subtract f from n n = n - fib[i]; // Move to Fibonacci just smaller than f i = i - 1 ; // Mark all Fibonacci > n as not used // (0 bit), progress backwards while (i >= 0 && fib[i] > n) { codeword[i] = '0' ; i = i - 1 ; } } // Additional '1' bit codeword[index + 1 ] = '1' ; codeword[index + 2 ] = ' ' ; String string = new String(codeword); // Return pointer to codeword return string; } // Driver code public static void main(String[] args) { int n = 143 ; System.out.println( "Fibonacci code word for " + n + " is " + fibonacciEncoding(n)); } } // This code is contributed by avanitrachhadiya2155 |
Python3
# Python3 program for Fibonacci Encoding # of a positive integer n # To limit on the largest # Fibonacci number to be used N = 30 # Array to store fibonacci numbers. # fib[i] is going to store # (i+2)'th Fibonacci number fib = [ 0 for i in range (N)] # Stores values in fib and returns index of # the largest fibonacci number smaller than n. def largestFiboLessOrEqual(n): fib[ 0 ] = 1 # Fib[0] stores 2nd Fibonacci No. fib[ 1 ] = 2 # Fib[1] stores 3rd Fibonacci No. # Keep Generating remaining numbers while # previously generated number is smaller i = 2 while fib[i - 1 ] < = n: fib[i] = fib[i - 1 ] + fib[i - 2 ] i + = 1 # Return index of the largest fibonacci number # smaller than or equal to n. Note that the above # loop stopped when fib[i-1] became larger. return (i - 2 ) # Returns pointer to the char string which # corresponds to code for n def fibonacciEncoding(n): index = largestFiboLessOrEqual(n) # allocate memory for codeword codeword = [ 'a' for i in range (index + 2 )] # index of the largest Fibonacci f <= n i = index while (n): # Mark usage of Fibonacci f (1 bit) codeword[i] = '1' # Subtract f from n n = n - fib[i] # Move to Fibonacci just smaller than f i = i - 1 # Mark all Fibonacci > n as not used (0 bit), # progress backwards while (i > = 0 and fib[i] > n): codeword[i] = '0' i = i - 1 # additional '1' bit codeword[index + 1 ] = '1' # return pointer to codeword return "".join(codeword) # Driver Code n = 143 print ( "Fibonacci code word for" , n, "is" , fibonacciEncoding(n)) # This code is contributed by Mohit Kumar |
C#
// C# program for Fibonacci Encoding // of a positive integer n using System; class GFG{ // To limit on the largest Fibonacci // number to be used public static int N = 30; // Array to store fibonacci numbers. // fib[i] is going to store (i+2)'th // Fibonacci number public static int [] fib = new int [N]; // Stores values in fib and returns index of // the largest fibonacci number smaller than n. public static int largestFiboLessOrEqual( int n) { // Fib[0] stores 2nd Fibonacci No. fib[0] = 1; // Fib[1] stores 3rd Fibonacci No. fib[1] = 2; // Keep Generating remaining numbers while // previously generated number is smaller int i; for (i = 2; fib[i - 1] <= n; i++) { fib[i] = fib[i - 1] + fib[i - 2]; } // Return index of the largest fibonacci // number smaller than or equal to n. // Note that the above loop stopped when // fib[i-1] became larger. return (i - 2); } // Returns pointer to the char string which // corresponds to code for n public static String fibonacciEncoding( int n) { int index = largestFiboLessOrEqual(n); // Allocate memory for codeword char [] codeword = new char [index + 3]; // Index of the largest Fibonacci f <= n int i = index; while (n > 0) { // Mark usage of Fibonacci f(1 bit) codeword[i] = '1' ; // Subtract f from n n = n - fib[i]; // Move to Fibonacci just smaller than f i = i - 1; // Mark all Fibonacci > n as not used // (0 bit), progress backwards while (i >= 0 && fib[i] > n) { codeword[i] = '0' ; i = i - 1; } } // Additional '1' bit codeword[index + 1] = '1' ; codeword[index + 2] = ' ' ; string str = new string (codeword); // Return pointer to codeword return str; } // Driver code static public void Main() { int n = 143; Console.WriteLine( "Fibonacci code word for " + n + " is " + fibonacciEncoding(n)); } } // This code is contributed by rag2127 |
Javascript
<script> // Javascript program for Fibonacci Encoding // of a positive integer n // To limit on the largest Fibonacci // number to be used let N = 30; // Array to store fibonacci numbers. // fib[i] is going to store (i+2)'th // Fibonacci number let fib = new Array(N); // Stores values in fib and returns index of // the largest fibonacci number smaller than n. function largestFiboLessOrEqual(n) { // Fib[0] stores 2nd Fibonacci No. fib[0] = 1; // Fib[1] stores 3rd Fibonacci No. fib[1] = 2; // Keep Generating remaining numbers while // previously generated number is smaller let i; for (i = 2; fib[i - 1] <= n; i++) { fib[i] = fib[i - 1] + fib[i - 2]; } // Return index of the largest fibonacci // number smaller than or equal to n. // Note that the above loop stopped when // fib[i-1] became larger. return (i - 2); } // Returns pointer to the char string which // corresponds to code for n function fibonacciEncoding(n) { let index = largestFiboLessOrEqual(n); // Allocate memory for codeword let codeword = new Array(index + 3); // Index of the largest Fibonacci f <= n let i = index; while (n > 0) { // Mark usage of Fibonacci f(1 bit) codeword[i] = '1 '; // Subtract f from n n = n - fib[i]; // Move to Fibonacci just smaller than f i = i - 1; // Mark all Fibonacci > n as not used // (0 bit), progress backwards while (i >= 0 && fib[i] > n) { codeword[i] = ' 0 '; i = i - 1; } } // Additional ' 1 ' bit codeword[index + 1] = ' 1 '; codeword[index + 2] = ' '; let string =(codeword).join( "" ); // Return pointer to codeword return string; } // Driver code let n = 143; document.write( "Fibonacci code word for " + n + " is " + fibonacciEncoding(n)); // This code is contributed by unknown2108 </script> |
输出:
Fibonacci code word for 143 is 01010101011
插图
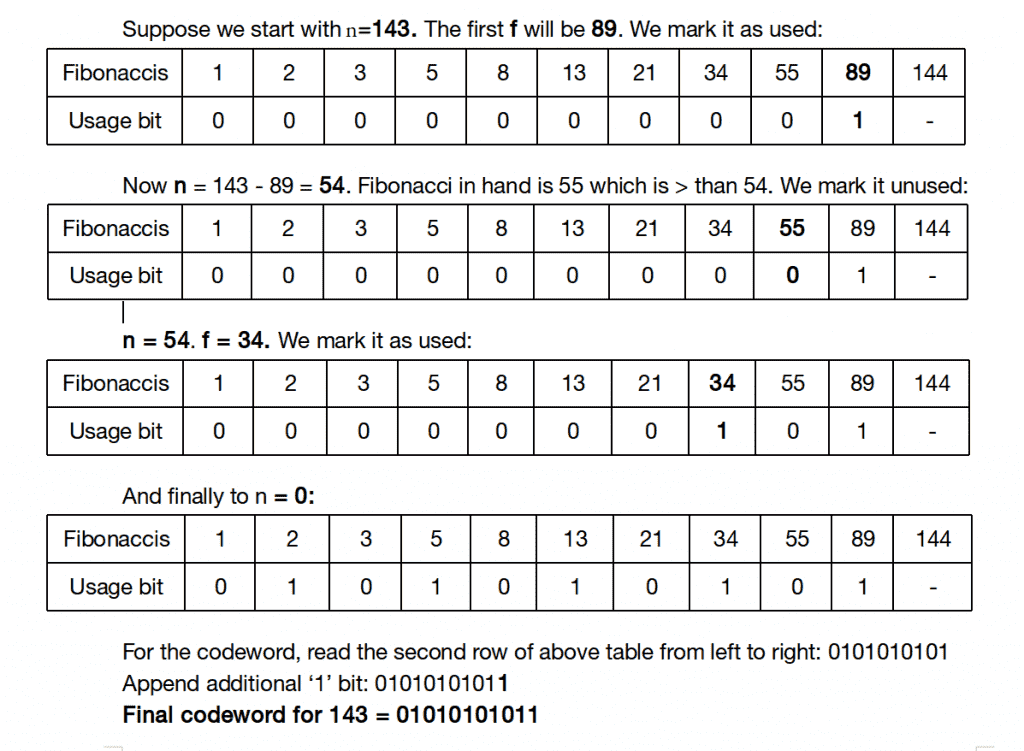
应用领域: 数据处理和压缩——以存储或传输数据所需的空间小于输入数据大小的方式表示数据(可以是文本、图像、视频等)。统计方法使用可变长度代码,将较短的代码分配给发生概率较高的符号或符号组。如果这些代码要在嘈杂的通信信道上使用,那么它们对位插入、删除和位翻转的恢复能力非常重要。 了解更多有关应用程序的信息 在这里 .
本文由 亚什·瓦里亚尼 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



