我们强烈建议将以下帖子作为这项工作的先决条件。 K维树|集1(搜索和插入) K维树|集2(求最小值) 本文讨论了删除。操作是从KD树中删除给定的点。
喜欢 二叉搜索树删除, 我们递归地向下遍历并搜索要删除的点。以下是访问的每个节点的步骤。
1) 如果当前节点包含要删除的点
- 如果要删除的节点是叶节点,只需删除它(与 BST删除 )
- 如果要删除的节点的右子节点为NOTNULL(不同于BST)
- 在右子树中查找当前节点维度的最小值。
- 用上面找到的最小值替换节点,并递归删除右子树中的最小值。
- 否则,如果要删除的节点将子节点保留为not NULL(不同于BST)
- 在左子树中查找当前节点维度的最小值。
- 用上面找到的最小值替换节点,并递归删除左子树中的最小值。
- 将新的左子树设为当前节点的右子树。
2) 如果当前不包含要删除的点
- 如果要删除的节点小于当前维度上的当前节点,则对左子树重复。
- 否则,右子树将重复出现。
为什么1。b和1。c和BST有什么不同? 在BST delete中,如果节点的左子节点为空,而右子节点不为空,我们将用右子节点替换该节点。在KD树中,这样做会违反KD树属性,因为节点的右子节点的维度与节点的维度不同。例如,如果节点将点除以x轴值。然后它的子节点除以y轴,所以我们不能简单地用正确的子节点替换节点。当右边的子项不为空,左边的子项为空时,情况也是如此。
为什么1。c在左子树中找不到最大值,并重复出现最大值,如1。B 这样做违反了所有相等的值都在右子树中的属性。例如,如果我们删除下面子树中的(!0,10),并将if替换为
Wrong Way (Equal key in left subtree after deletion)
(5, 6) (4, 10)
/ Delete(5, 6) /
(4, 10) ------------> (4, 20)
(4, 20)
Right way (Equal key in right subtree after deletion)
(5, 6) (4, 10)
/ Delete(5, 6)
(4, 10) ------------> (4, 20)
(4, 20)
删除示例: Delete(30,40):由于右子节点不为NULL,且节点的维数为x,因此我们在右子节点中找到具有最小x值的节点。节点是(35,45),我们将(30,40)替换为(35,45)并删除(30,40)。

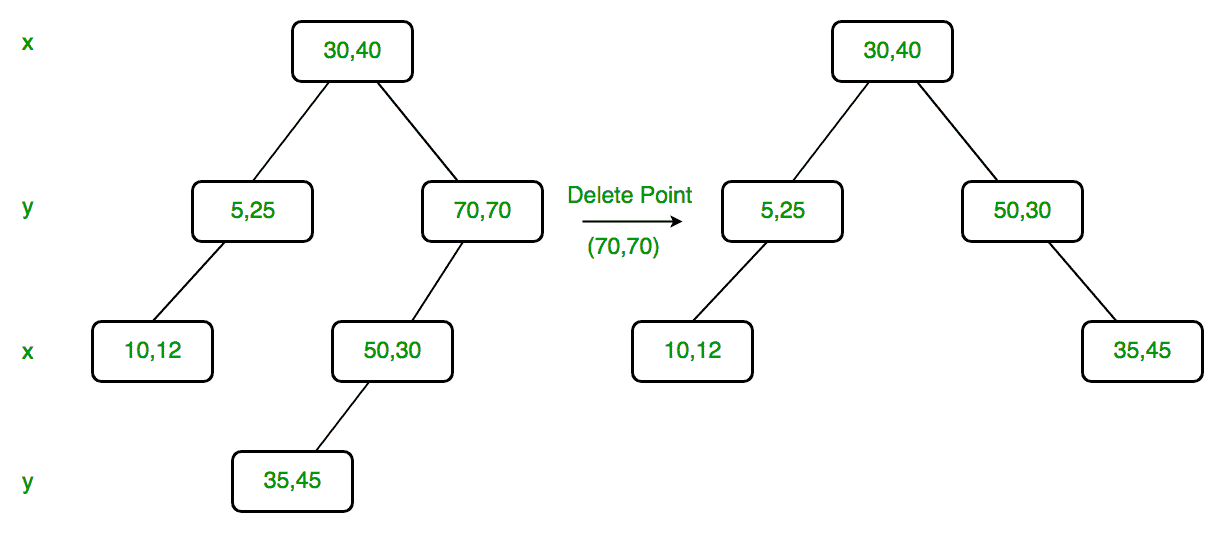
Delete(70,70):节点的维数为y。由于右子节点为空,我们在左子节点中找到y值最小的节点。节点是(50,30),我们用(50,30)替换(70,70),并递归删除左子树中的(50,30)。最后,我们将修改后的左子树作为(50,30)的右子树。
下面是C++实现的K D树的删除。
C++
// A C++ program to demonstrate delete in K D tree #include<bits/stdc++.h> using namespace std; const int k = 2; // A structure to represent node of kd tree struct Node { int point[k]; // To store k dimensional point Node *left, *right; }; // A method to create a node of K D tree struct Node* newNode( int arr[]) { struct Node* temp = new Node; for ( int i=0; i<k; i++) temp->point[i] = arr[i]; temp->left = temp->right = NULL; return temp; } // Inserts a new node and returns root of modified tree // The parameter depth is used to decide axis of comparison Node *insertRec(Node *root, int point[], unsigned depth) { // Tree is empty? if (root == NULL) return newNode(point); // Calculate current dimension (cd) of comparison unsigned cd = depth % k; // Compare the new point with root on current dimension 'cd' // and decide the left or right subtree if (point[cd] < (root->point[cd])) root->left = insertRec(root->left, point, depth + 1); else root->right = insertRec(root->right, point, depth + 1); return root; } // Function to insert a new point with given point in // KD Tree and return new root. It mainly uses above recursive // function "insertRec()" Node* insert(Node *root, int point[]) { return insertRec(root, point, 0); } // A utility function to find minimum of three integers Node *minNode(Node *x, Node *y, Node *z, int d) { Node *res = x; if (y != NULL && y->point[d] < res->point[d]) res = y; if (z != NULL && z->point[d] < res->point[d]) res = z; return res; } // Recursively finds minimum of d'th dimension in KD tree // The parameter depth is used to determine current axis. Node *findMinRec(Node* root, int d, unsigned depth) { // Base cases if (root == NULL) return NULL; // Current dimension is computed using current depth and total // dimensions (k) unsigned cd = depth % k; // Compare point with root with respect to cd (Current dimension) if (cd == d) { if (root->left == NULL) return root; return findMinRec(root->left, d, depth+1); } // If current dimension is different then minimum can be anywhere // in this subtree return minNode(root, findMinRec(root->left, d, depth+1), findMinRec(root->right, d, depth+1), d); } // A wrapper over findMinRec(). Returns minimum of d'th dimension Node *findMin(Node* root, int d) { // Pass current level or depth as 0 return findMinRec(root, d, 0); } // A utility method to determine if two Points are same // in K Dimensional space bool arePointsSame( int point1[], int point2[]) { // Compare individual pointinate values for ( int i = 0; i < k; ++i) if (point1[i] != point2[i]) return false ; return true ; } // Copies point p2 to p1 void copyPoint( int p1[], int p2[]) { for ( int i=0; i<k; i++) p1[i] = p2[i]; } // Function to delete a given point 'point[]' from tree with root // as 'root'. depth is current depth and passed as 0 initially. // Returns root of the modified tree. Node *deleteNodeRec(Node *root, int point[], int depth) { // Given point is not present if (root == NULL) return NULL; // Find dimension of current node int cd = depth % k; // If the point to be deleted is present at root if (arePointsSame(root->point, point)) { // 2.b) If right child is not NULL if (root->right != NULL) { // Find minimum of root's dimension in right subtree Node *min = findMin(root->right, cd); // Copy the minimum to root copyPoint(root->point, min->point); // Recursively delete the minimum root->right = deleteNodeRec(root->right, min->point, depth+1); } else if (root->left != NULL) // same as above { Node *min = findMin(root->left, cd); copyPoint(root->point, min->point); root->right = deleteNodeRec(root->left, min->point, depth+1); } else // If node to be deleted is leaf node { delete root; return NULL; } return root; } // 2) If current node doesn't contain point, search downward if (point[cd] < root->point[cd]) root->left = deleteNodeRec(root->left, point, depth+1); else root->right = deleteNodeRec(root->right, point, depth+1); return root; } // Function to delete a given point from K D Tree with 'root' Node* deleteNode(Node *root, int point[]) { // Pass depth as 0 return deleteNodeRec(root, point, 0); } // Driver program to test above functions int main() { struct Node *root = NULL; int points[][k] = {{30, 40}, {5, 25}, {70, 70}, {10, 12}, {50, 30}, {35, 45}}; int n = sizeof (points)/ sizeof (points[0]); for ( int i=0; i<n; i++) root = insert(root, points[i]); // Delete (30, 40); root = deleteNode(root, points[0]); cout << "Root after deletion of (30, 40)" ; cout << root->point[0] << ", " << root->point[1] << endl; return 0; } |
输出:
Root after deletion of (30, 40) 35, 45
资料来源: https://www.cs.umd.edu/class/spring2008/cmsc420/L19.kd-trees.pdf 本文由 阿什什·古普塔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



