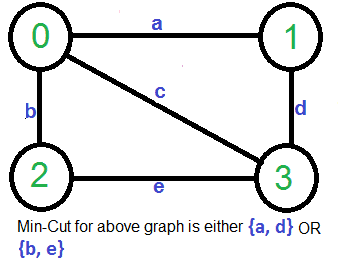
给定一个无向且未加权的图,找到最小割(将图断开为两个分量的边的最小数目)。 输入图形可能有平行边。 例如,考虑下面的例子,最小的切口有2个边。
一个简单的解决方案 基于最大流的 s-t割算法 找到最小切割。考虑每一对顶点作为源S′和S′T,并调用最小S T割算法找到S T割。返回所有s-t切割的最小值。该算法的最佳时间复杂度为O(V) 5. )一张图表。[怎么做?总有可能是V 2. 配对和一对的s-t切割算法需要O(V*E)时间,E=O(V 2. )]. 下面是简单的卡格算法。下面,卡格的算法可以用O(E)=O(V)实现 2. )时间到了。
1) Initialize contracted graph CG as copy of original graph2) While there are more than 2 vertices. a) Pick a random edge (u, v) in the contracted graph. b) Merge (or contract) u and v into a single vertex (update the contracted graph). c) Remove self-loops3) Return cut represented by two vertices.
让我们通过给出的例子来理解上述算法。 让第一个随机拾取的顶点为’ A. ‘连接顶点0和1。我们移除这条边并收缩图(合并顶点0和1)。我们得到下面的图表。
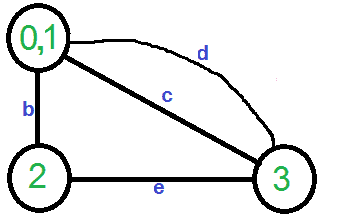
让下一个随机选取的边为“d”。我们移除这条边并合并顶点(0,1)和3。
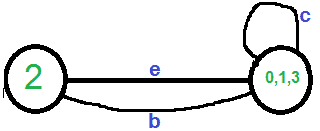
我们需要删除图中的自循环。所以我们去掉边“c”
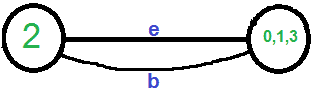
现在图形有两个顶点,所以我们停止。结果图中的边数是由Karger算法生成的割。 卡格算法是一种 蒙特卡罗算法 它产生的切割可能不是最小的。 例如,下图显示了拾取随机边的不同顺序会产生大小为3的最小切割。

下面是C++实现上述算法。输入图形表示为边和边的集合 联合查找数据结构 用于跟踪组件。
C
// Karger's algorithm to find Minimum Cut in an // undirected, unweighted and connected graph. #include <stdio.h> #include <stdlib.h> #include <time.h> // a structure to represent a unweighted edge in graph struct Edge { int src, dest; }; // a structure to represent a connected, undirected // and unweighted graph as a collection of edges. struct Graph { // V-> Number of vertices, E-> Number of edges int V, E; // graph is represented as an array of edges. // Since the graph is undirected, the edge // from src to dest is also edge from dest // to src. Both are counted as 1 edge here. Edge* edge; }; // A structure to represent a subset for union-find struct subset { int parent; int rank; }; // Function prototypes for union-find (These functions are defined // after kargerMinCut() ) int find( struct subset subsets[], int i); void Union( struct subset subsets[], int x, int y); // A very basic implementation of Karger's randomized // algorithm for finding the minimum cut. Please note // that Karger's algorithm is a Monte Carlo Randomized algo // and the cut returned by the algorithm may not be // minimum always int kargerMinCut( struct Graph* graph) { // Get data of given graph int V = graph->V, E = graph->E; Edge *edge = graph->edge; // Allocate memory for creating V subsets. struct subset *subsets = new subset[V]; // Create V subsets with single elements for ( int v = 0; v < V; ++v) { subsets[v].parent = v; subsets[v].rank = 0; } // Initially there are V vertices in // contracted graph int vertices = V; // Keep contracting vertices until there are // 2 vertices. while (vertices > 2) { // Pick a random edge int i = rand () % E; // Find vertices (or sets) of two corners // of current edge int subset1 = find(subsets, edge[i].src); int subset2 = find(subsets, edge[i].dest); // If two corners belong to same subset, // then no point considering this edge if (subset1 == subset2) continue ; // Else contract the edge (or combine the // corners of edge into one vertex) else { printf ( "Contracting edge %d-%d" , edge[i].src, edge[i].dest); vertices--; Union(subsets, subset1, subset2); } } // Now we have two vertices (or subsets) left in // the contracted graph, so count the edges between // two components and return the count. int cutedges = 0; for ( int i=0; i<E; i++) { int subset1 = find(subsets, edge[i].src); int subset2 = find(subsets, edge[i].dest); if (subset1 != subset2) cutedges++; } return cutedges; } // A utility function to find set of an element i // (uses path compression technique) int find( struct subset subsets[], int i) { // find root and make root as parent of i // (path compression) if (subsets[i].parent != i) subsets[i].parent = find(subsets, subsets[i].parent); return subsets[i].parent; } // A function that does union of two sets of x and y // (uses union by rank) void Union( struct subset subsets[], int x, int y) { int xroot = find(subsets, x); int yroot = find(subsets, y); // Attach smaller rank tree under root of high // rank tree (Union by Rank) if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot; // If ranks are same, then make one as root and // increment its rank by one else { subsets[yroot].parent = xroot; subsets[xroot].rank++; } } // Creates a graph with V vertices and E edges struct Graph* createGraph( int V, int E) { Graph* graph = new Graph; graph->V = V; graph->E = E; graph->edge = new Edge[E]; return graph; } // Driver program to test above functions int main() { /* Let us create following unweighted graph 0------1 | | | | | | 2------3 */ int V = 4; // Number of vertices in graph int E = 5; // Number of edges in graph struct Graph* graph = createGraph(V, E); // add edge 0-1 graph->edge[0].src = 0; graph->edge[0].dest = 1; // add edge 0-2 graph->edge[1].src = 0; graph->edge[1].dest = 2; // add edge 0-3 graph->edge[2].src = 0; graph->edge[2].dest = 3; // add edge 1-3 graph->edge[3].src = 1; graph->edge[3].dest = 3; // add edge 2-3 graph->edge[4].src = 2; graph->edge[4].dest = 3; // Use a different seed value for every run. srand ( time (NULL)); printf ( "Cut found by Karger's randomized algo is %d" , kargerMinCut(graph)); return 0; } |
输出:
Contracting edge 0-2Contracting edge 0-3Cut found by Karger's randomized algo is 2
请注意,上述程序基于随机函数的结果,可能会产生不同的输出。 在这篇文章中,我们讨论了简单的卡格算法,并发现该算法并不总是产生最小割。上述算法产生的最小割概率大于或等于1/(n) 2. ).见下一篇文章 Karger算法的分析与应用 文中还讨论了这一概率的应用、证明和改进。 参考资料: http://en.wikipedia.org/wiki/Karger%27s_algorithm https://www.youtube.com/watch?v=P0l8jMDQTEQ https://www.cs.princeton.edu/courses/archive/fall13/cos521/lecnotes/lec2final.pdf http://web.stanford.edu/class/archive/cs/cs161/cs161.1138/lectures/11/Small11.pdf 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



