让我们考虑下面的问题来理解二叉索引树。 我们有一个数组arr[0…n-1]。我们想 1. 计算前i个元素的和。 2. 修改数组arr[i]=x的指定元素的值,其中0<=i<=n-1。 A. 简单解决方案 就是运行一个从0到i-1的循环,并计算元素之和。要更新一个值,只需执行arr[i]=x。第一个操作需要O(n)时间,第二个操作需要O(1)时间。另一个简单的解决方案是创建一个额外的数组,并在这个新数组的第i个索引处存储第一个第i个元素的总和。给定范围的总和现在可以在O(1)时间内计算,但更新操作现在需要O(n)时间。如果有大量的查询操作,但只有很少的更新操作,那么这种方法很有效。 我们能在O(logn)时间内执行查询和更新操作吗? 一个有效的解决方案是使用 分段树 在O(Logn)时间内执行这两个操作。 另一种解决方案是二叉索引树,这两种操作的时间复杂度都达到了O(Logn)。与分段树相比,二叉索引树需要更少的空间,更容易实现。 . 代表 二叉索引树表示为一个数组。让数组为BITree[]。二叉索引树的每个节点都存储输入数组中某些元素的总和。二叉索引树的大小等于输入数组的大小,表示为n。在下面的代码中,为了便于实现,我们使用了n+1的大小。 建设 我们将BITree[]中的所有值初始化为0。然后我们为所有索引调用update(),下面讨论update()操作。 操作
getSum(x):返回子数组arr[0,…,x]的和 //返回使用比特树[0..n]的子数组arr[0,…,x]的和,该比特树是由arr[0..n-1]构造的 1) 将输出和初始化为0,当前索引初始化为x+1。 2) 当当前索引大于0时执行以下操作。 …a)将BITree[索引]添加到总和 …b)转到BITree[index]的父级。可以通过删除 当前索引的最后一个设置位,即索引=索引–(索引和(-index)) 3) 返回总数。

上图提供了getSum()如何工作的示例。以下是一些重要的观察结果。 BITree[0]是一个虚拟节点。 BITree[y]是BITree[x]的父元素,当且仅当y可以通过从x的二进制表示中移除最后一个设置位来获得,即y=x–(x&-x)。 节点BITree[y]的子节点BITree[x]存储y(包含)和x(排除)之间的元素之和:arr[y,…,x)。
更新(x,val):通过执行arr[index]+=val更新二叉索引树(BIT) //请注意,更新(x,val)操作不会更改arr[]。它只对BITree[]进行更改 1) 将当前索引初始化为x+1。 2) 当当前索引小于或等于n时,执行以下操作。 …a)将val添加到BITree[索引] …b)转到BITree[索引]的下一个元素。下一个元素可以通过增加当前索引的最后一个设置位来获得,即index=index+(index&(-index))
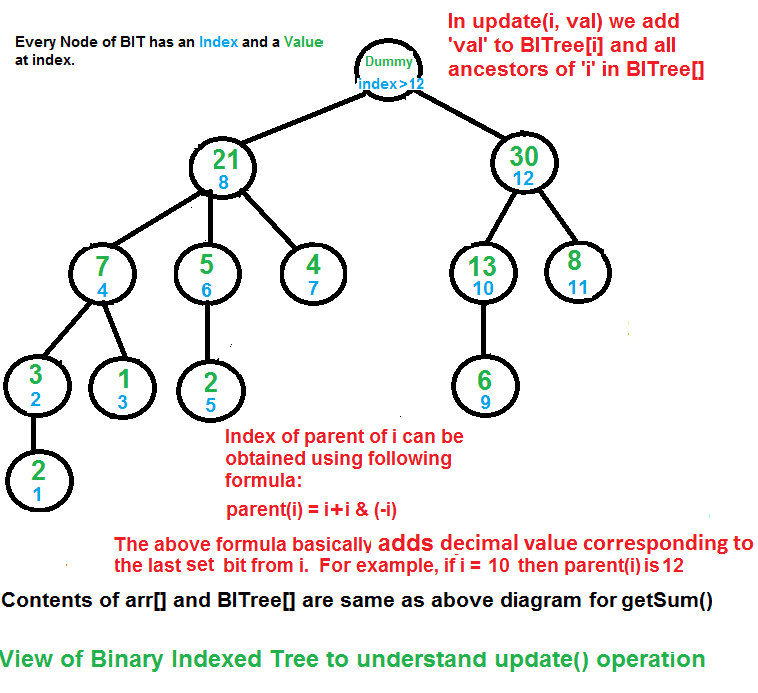
update函数需要确保更新其范围内包含arr[i]的所有比特树节点。我们通过重复添加与当前索引的最后一个设置位对应的十进制数,在比特树中循环这些节点。 二叉索引树是如何工作的? 这个想法基于这样一个事实:所有正整数都可以表示为2的幂和。例如,19可以表示为16+2+1。比特树的每个节点存储n个元素的总和,其中n是2的幂。例如,在上面的第一个图表(getSum()的图表)中,前12个元素的总和可以通过最后4个元素(从9到12)的总和加上8个元素(从1到8)的总和来获得。一个数n的二进制表示中的设置位数是O(Logn)。因此,我们在getSum()和update()操作中最多遍历O(Logn)个节点。构造的时间复杂度是O(nLogn),因为它对所有n个元素调用update()。 实施: 以下是二叉索引树的实现。
C++
// C++ code to demonstrate operations of Binary Index Tree #include <iostream> using namespace std; /* n --> No. of elements present in input array. BITree[0..n] --> Array that represents Binary Indexed Tree. arr[0..n-1] --> Input array for which prefix sum is evaluated. */ // Returns sum of arr[0..index]. This function assumes // that the array is preprocessed and partial sums of // array elements are stored in BITree[]. int getSum( int BITree[], int index) { int sum = 0; // Initialize result // index in BITree[] is 1 more than the index in arr[] index = index + 1; // Traverse ancestors of BITree[index] while (index>0) { // Add current element of BITree to sum sum += BITree[index]; // Move index to parent node in getSum View index -= index & (-index); } return sum; } // Updates a node in Binary Index Tree (BITree) at given index // in BITree. The given value 'val' is added to BITree[i] and // all of its ancestors in tree. void updateBIT( int BITree[], int n, int index, int val) { // index in BITree[] is 1 more than the index in arr[] index = index + 1; // Traverse all ancestors and add 'val' while (index <= n) { // Add 'val' to current node of BI Tree BITree[index] += val; // Update index to that of parent in update View index += index & (-index); } } // Constructs and returns a Binary Indexed Tree for given // array of size n. int *constructBITree( int arr[], int n) { // Create and initialize BITree[] as 0 int *BITree = new int [n+1]; for ( int i=1; i<=n; i++) BITree[i] = 0; // Store the actual values in BITree[] using update() for ( int i=0; i<n; i++) updateBIT(BITree, n, i, arr[i]); // Uncomment below lines to see contents of BITree[] //for (int i=1; i<=n; i++) // cout << BITree[i] << " "; return BITree; } // Driver program to test above functions int main() { int freq[] = {2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9}; int n = sizeof (freq)/ sizeof (freq[0]); int *BITree = constructBITree(freq, n); cout << "Sum of elements in arr[0..5] is " << getSum(BITree, 5); // Let use test the update operation freq[3] += 6; updateBIT(BITree, n, 3, 6); //Update BIT for above change in arr[] cout << "Sum of elements in arr[0..5] after update is " << getSum(BITree, 5); return 0; } |
JAVA
// Java program to demonstrate lazy // propagation in segment tree import java.util.*; import java.lang.*; import java.io.*; class BinaryIndexedTree { // Max tree size final static int MAX = 1000 ; static int BITree[] = new int [MAX]; /* n --> No. of elements present in input array. BITree[0..n] --> Array that represents Binary Indexed Tree. arr[0..n-1] --> Input array for which prefix sum is evaluated. */ // Returns sum of arr[0..index]. This function // assumes that the array is preprocessed and // partial sums of array elements are stored // in BITree[]. int getSum( int index) { int sum = 0 ; // Initialize result // index in BITree[] is 1 more than // the index in arr[] index = index + 1 ; // Traverse ancestors of BITree[index] while (index> 0 ) { // Add current element of BITree // to sum sum += BITree[index]; // Move index to parent node in // getSum View index -= index & (-index); } return sum; } // Updates a node in Binary Index Tree (BITree) // at given index in BITree. The given value // 'val' is added to BITree[i] and all of // its ancestors in tree. public static void updateBIT( int n, int index, int val) { // index in BITree[] is 1 more than // the index in arr[] index = index + 1 ; // Traverse all ancestors and add 'val' while (index <= n) { // Add 'val' to current node of BIT Tree BITree[index] += val; // Update index to that of parent // in update View index += index & (-index); } } /* Function to construct fenwick tree from given array.*/ void constructBITree( int arr[], int n) { // Initialize BITree[] as 0 for ( int i= 1 ; i<=n; i++) BITree[i] = 0 ; // Store the actual values in BITree[] // using update() for ( int i = 0 ; i < n; i++) updateBIT(n, i, arr[i]); } // Main function public static void main(String args[]) { int freq[] = { 2 , 1 , 1 , 3 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }; int n = freq.length; BinaryIndexedTree tree = new BinaryIndexedTree(); // Build fenwick tree from given array tree.constructBITree(freq, n); System.out.println( "Sum of elements in arr[0..5]" + " is " + tree.getSum( 5 )); // Let use test the update operation freq[ 3 ] += 6 ; // Update BIT for above change in arr[] updateBIT(n, 3 , 6 ); // Find sum after the value is updated System.out.println( "Sum of elements in arr[0..5]" + " after update is " + tree.getSum( 5 )); } } // This code is contributed by Ranjan Binwani |
Python3
# Python implementation of Binary Indexed Tree # Returns sum of arr[0..index]. This function assumes # that the array is preprocessed and partial sums of # array elements are stored in BITree[]. def getsum(BITTree,i): s = 0 #initialize result # index in BITree[] is 1 more than the index in arr[] i = i + 1 # Traverse ancestors of BITree[index] while i > 0 : # Add current element of BITree to sum s + = BITTree[i] # Move index to parent node in getSum View i - = i & ( - i) return s # Updates a node in Binary Index Tree (BITree) at given index # in BITree. The given value 'val' is added to BITree[i] and # all of its ancestors in tree. def updatebit(BITTree , n , i ,v): # index in BITree[] is 1 more than the index in arr[] i + = 1 # Traverse all ancestors and add 'val' while i < = n: # Add 'val' to current node of BI Tree BITTree[i] + = v # Update index to that of parent in update View i + = i & ( - i) # Constructs and returns a Binary Indexed Tree for given # array of size n. def construct(arr, n): # Create and initialize BITree[] as 0 BITTree = [ 0 ] * (n + 1 ) # Store the actual values in BITree[] using update() for i in range (n): updatebit(BITTree, n, i, arr[i]) # Uncomment below lines to see contents of BITree[] #for i in range(1,n+1): # print BITTree[i], return BITTree # Driver code to test above methods freq = [ 2 , 1 , 1 , 3 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ] BITTree = construct(freq, len (freq)) print ( "Sum of elements in arr[0..5] is " + str (getsum(BITTree, 5 ))) freq[ 3 ] + = 6 updatebit(BITTree, len (freq), 3 , 6 ) print ( "Sum of elements in arr[0..5]" + " after update is " + str (getsum(BITTree, 5 ))) # This code is contributed by Raju Varshney |
C#
// C# program to demonstrate lazy // propagation in segment tree using System; public class BinaryIndexedTree { // Max tree size readonly static int MAX = 1000; static int []BITree = new int [MAX]; /* n --> No. of elements present in input array. BITree[0..n] --> Array that represents Binary Indexed Tree. arr[0..n-1] --> Input array for which prefix sum is evaluated. */ // Returns sum of arr[0..index]. This function // assumes that the array is preprocessed and // partial sums of array elements are stored // in BITree[]. int getSum( int index) { int sum = 0; // Initialize result // index in BITree[] is 1 more than // the index in arr[] index = index + 1; // Traverse ancestors of BITree[index] while (index>0) { // Add current element of BITree // to sum sum += BITree[index]; // Move index to parent node in // getSum View index -= index & (-index); } return sum; } // Updates a node in Binary Index Tree (BITree) // at given index in BITree. The given value // 'val' is added to BITree[i] and all of // its ancestors in tree. public static void updateBIT( int n, int index, int val) { // index in BITree[] is 1 more than // the index in arr[] index = index + 1; // Traverse all ancestors and add 'val' while (index <= n) { // Add 'val' to current node of BIT Tree BITree[index] += val; // Update index to that of parent // in update View index += index & (-index); } } /* Function to construct fenwick tree from given array.*/ void constructBITree( int []arr, int n) { // Initialize BITree[] as 0 for ( int i = 1; i <= n; i++) BITree[i] = 0; // Store the actual values in BITree[] // using update() for ( int i = 0; i < n; i++) updateBIT(n, i, arr[i]); } // Driver code public static void Main(String []args) { int []freq = {2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9}; int n = freq.Length; BinaryIndexedTree tree = new BinaryIndexedTree(); // Build fenwick tree from given array tree.constructBITree(freq, n); Console.WriteLine( "Sum of elements in arr[0..5]" + " is " + tree.getSum(5)); // Let use test the update operation freq[3] += 6; // Update BIT for above change in arr[] updateBIT(n, 3, 6); // Find sum after the value is updated Console.WriteLine( "Sum of elements in arr[0..5]" + " after update is " + tree.getSum(5)); } } // This code is contributed by PrinciRaj1992 |
Javascript
<script> // Javascript program to demonstrate lazy // propagation in segment tree // Max tree size let MAX = 1000; let BITree= new Array(MAX); /* n --> No. of elements present in input array. BITree[0..n] --> Array that represents Binary Indexed Tree. arr[0..n-1] --> Input array for which prefix sum is evaluated. */ // Returns sum of arr[0..index]. This function // assumes that the array is preprocessed and // partial sums of array elements are stored // in BITree[]. function getSum( index) { let sum = 0; // Initialize result // index in BITree[] is 1 more than // the index in arr[] index = index + 1; // Traverse ancestors of BITree[index] while (index>0) { // Add current element of BITree // to sum sum += BITree[index]; // Move index to parent node in // getSum View index -= index & (-index); } return sum; } // Updates a node in Binary Index Tree (BITree) // at given index in BITree. The given value // 'val' is added to BITree[i] and all of // its ancestors in tree. function updateBIT(n,index,val) { // index in BITree[] is 1 more than // the index in arr[] index = index + 1; // Traverse all ancestors and add 'val' while (index <= n) { // Add 'val' to current node of BIT Tree BITree[index] += val; // Update index to that of parent // in update View index += index & (-index); } } /* Function to construct fenwick tree from given array.*/ function constructBITree(arr,n) { // Initialize BITree[] as 0 for (let i=1; i<=n; i++) BITree[i] = 0; // Store the actual values in BITree[] // using update() for (let i = 0; i < n; i++) updateBIT(n, i, arr[i]); } // Main function let freq=[2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9]; let n = freq.length; // Build fenwick tree from given array constructBITree(freq, n); document.write( "Sum of elements in arr[0..5]" + " is " + getSum(5)+ "<br>" ); // Let use test the update operation freq[3] += 6; // Update BIT for above change in arr[] updateBIT(n, 3, 6); // Find sum after the value is updated document.write( "Sum of elements in arr[0..5]" + " after update is " + getSum(5)); // This code is contributed by patel2127 </script> |
输出:
Sum of elements in arr[0..5] is 12Sum of elements in arr[0..5] after update is 18
我们能把二叉索引树扩展到计算O(Logn)时间范围的和吗? 对rangeSum(l,r)=getSum(r)–getSum(l-1)。 应用: 算术编码算法的实现。二叉索引树的发展主要是因为它在本例中的应用。看见 这 更多细节。 示例问题: 在数组|集合3中计数反转(使用位) 二维二叉索引树或Fenwick树 用BIT计算矩形空间中的三角形
参考资料: http://en.wikipedia.org/wiki/Fenwick_tree http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=binaryIndexedTrees 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



