给定二叉树、二叉树中的目标节点和整数值k,打印距离给定目标节点k的所有节点。没有可用的父指针。
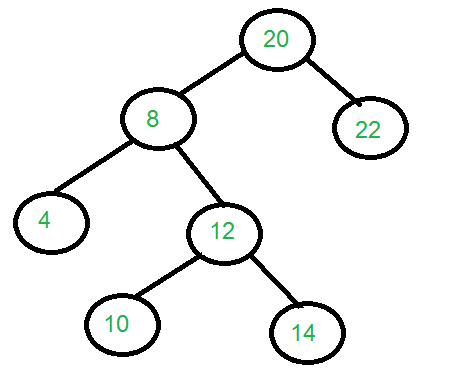
考虑图中所示的树 输入:target=指向包含数据8的节点的指针。 root=指向包含数据20的节点的指针。 k=2。 产出:101422 如果目标为14,k为3,则输出 应该是“420”
需要考虑两种类型的节点。 1) 子树中以目标节点为根的节点。例如,如果目标节点是8,k是2,那么这样的节点是10和14。 2) 其他节点,可能是目标的祖先,或其他子树中的节点。对于目标节点8和k为2,节点22属于该类别。 找到第一类节点很容易实现。只需遍历以目标节点为根的子树,并在递归调用中递减k。当k变为0时,打印当前正在遍历的节点(请参见 这 更多细节)。这里我们把函数称为 printkdistanceNodeDown() . 如何找到第二种类型的节点?对于不在以目标节点为根的子树中的输出节点,我们必须遍历所有祖先。对于每个祖先,我们找到它与目标节点的距离,让距离为d,现在我们转到祖先的其他子树(如果目标在左子树中找到,那么我们转到右子树,反之亦然),并找到与祖先在k-d距离处的所有节点。
以下是上述方法的实现。
C++
#include <iostream> using namespace std; // A binary Tree node struct node { int data; struct node *left, *right; }; /* Recursive function to print all the nodes at distance k in the tree (or subtree) rooted with given root. See */ void printkdistanceNodeDown(node *root, int k) { // Base Case if (root == NULL || k < 0) return ; // If we reach a k distant node, print it if (k==0) { cout << root->data << endl; return ; } // Recur for left and right subtrees printkdistanceNodeDown(root->left, k-1); printkdistanceNodeDown(root->right, k-1); } // Prints all nodes at distance k from a given target node. // The k distant nodes may be upward or downward. This function // Returns distance of root from target node, it returns -1 if target // node is not present in tree rooted with root. int printkdistanceNode(node* root, node* target , int k) { // Base Case 1: If tree is empty, return -1 if (root == NULL) return -1; // If target is same as root. Use the downward function // to print all nodes at distance k in subtree rooted with // target or root if (root == target) { printkdistanceNodeDown(root, k); return 0; } // Recur for left subtree int dl = printkdistanceNode(root->left, target, k); // Check if target node was found in left subtree if (dl != -1) { // If root is at distance k from target, print root // Note that dl is Distance of root's left child from target if (dl + 1 == k) cout << root->data << endl; // Else go to right subtree and print all k-dl-2 distant nodes // Note that the right child is 2 edges away from left child else printkdistanceNodeDown(root->right, k-dl-2); // Add 1 to the distance and return value for parent calls return 1 + dl; } // MIRROR OF ABOVE CODE FOR RIGHT SUBTREE // Note that we reach here only when node was not found in left subtree int dr = printkdistanceNode(root->right, target, k); if (dr != -1) { if (dr + 1 == k) cout << root->data << endl; else printkdistanceNodeDown(root->left, k-dr-2); return 1 + dr; } // If target was neither present in left nor in right subtree return -1; } // A utility function to create a new binary tree node node *newnode( int data) { node *temp = new node; temp->data = data; temp->left = temp->right = NULL; return temp; } // Driver program to test above functions int main() { /* Let us construct the tree shown in above diagram */ node * root = newnode(20); root->left = newnode(8); root->right = newnode(22); root->left->left = newnode(4); root->left->right = newnode(12); root->left->right->left = newnode(10); root->left->right->right = newnode(14); node * target = root->left->right; printkdistanceNode(root, target, 2); return 0; } |
JAVA
// Java program to print all nodes at a distance k from given node // A binary tree node class Node { int data; Node left, right; Node( int item) { data = item; left = right = null ; } } class BinaryTree { Node root; /* Recursive function to print all the nodes at distance k in tree (or subtree) rooted with given root. */ void printkdistanceNodeDown(Node node, int k) { // Base Case if (node == null || k < 0 ) return ; // If we reach a k distant node, print it if (k == 0 ) { System.out.print(node.data); System.out.println( "" ); return ; } // Recur for left and right subtrees printkdistanceNodeDown(node.left, k - 1 ); printkdistanceNodeDown(node.right, k - 1 ); } // Prints all nodes at distance k from a given target node. // The k distant nodes may be upward or downward.This function // Returns distance of root from target node, it returns -1 // if target node is not present in tree rooted with root. int printkdistanceNode(Node node, Node target, int k) { // Base Case 1: If tree is empty, return -1 if (node == null ) return - 1 ; // If target is same as root. Use the downward function // to print all nodes at distance k in subtree rooted with // target or root if (node == target) { printkdistanceNodeDown(node, k); return 0 ; } // Recur for left subtree int dl = printkdistanceNode(node.left, target, k); // Check if target node was found in left subtree if (dl != - 1 ) { // If root is at distance k from target, print root // Note that dl is Distance of root's left child from // target if (dl + 1 == k) { System.out.print(node.data); System.out.println( "" ); } // Else go to right subtree and print all k-dl-2 distant nodes // Note that the right child is 2 edges away from left child else printkdistanceNodeDown(node.right, k - dl - 2 ); // Add 1 to the distance and return value for parent calls return 1 + dl; } // MIRROR OF ABOVE CODE FOR RIGHT SUBTREE // Note that we reach here only when node was not found in left // subtree int dr = printkdistanceNode(node.right, target, k); if (dr != - 1 ) { if (dr + 1 == k) { System.out.print(node.data); System.out.println( "" ); } else printkdistanceNodeDown(node.left, k - dr - 2 ); return 1 + dr; } // If target was neither present in left nor in right subtree return - 1 ; } // Driver program to test the above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); /* Let us construct the tree shown in above diagram */ tree.root = new Node( 20 ); tree.root.left = new Node( 8 ); tree.root.right = new Node( 22 ); tree.root.left.left = new Node( 4 ); tree.root.left.right = new Node( 12 ); tree.root.left.right.left = new Node( 10 ); tree.root.left.right.right = new Node( 14 ); Node target = tree.root.left.right; tree.printkdistanceNode(tree.root, target, 2 ); } } // This code has been contributed by Mayank Jaiswal |
Python3
# Python program to print nodes at distance k from a given node # A binary tree node class Node: # A constructor to create a new node def __init__( self , data): self .data = data self .left = None self .right = None # Recursive function to print all the nodes at distance k # int the tree(or subtree) rooted with given root. See def printkDistanceNodeDown(root, k): # Base Case if root is None or k< 0 : return # If we reach a k distant node, print it if k = = 0 : print (root.data) return # Recur for left and right subtree printkDistanceNodeDown(root.left, k - 1 ) printkDistanceNodeDown(root.right, k - 1 ) # Prints all nodes at distance k from a given target node # The k distant nodes may be upward or downward. This function # returns distance of root from target node, it returns -1 # if target node is not present in tree rooted with root def printkDistanceNode(root, target, k): # Base Case 1 : IF tree is empty return -1 if root is None : return - 1 # If target is same as root. Use the downward function # to print all nodes at distance k in subtree rooted with # target or root if root = = target: printkDistanceNodeDown(root, k) return 0 # Recur for left subtree dl = printkDistanceNode(root.left, target, k) # Check if target node was found in left subtree if dl ! = - 1 : # If root is at distance k from target, print root # Note: dl is distance of root's left child # from target if dl + 1 = = k : print (root.data) # Else go to right subtreee and print all k-dl-2 # distant nodes # Note: that the right child is 2 edges away from # left child else : printkDistanceNodeDown(root.right, k - dl - 2 ) # Add 1 to the distance and return value for # for parent calls return 1 + dl # MIRROR OF ABOVE CODE FOR RIGHT SUBTREE # Note that we reach here only when node was not found # in left subtree dr = printkDistanceNode(root.right, target, k) if dr ! = - 1 : if (dr + 1 = = k): print (root.data) else : printkDistanceNodeDown(root.left, k - dr - 2 ) return 1 + dr # If target was neither present in left nor in right subtree return - 1 # Driver program to test above function root = Node( 20 ) root.left = Node( 8 ) root.right = Node( 22 ) root.left.left = Node( 4 ) root.left.right = Node( 12 ) root.left.right.left = Node( 10 ) root.left.right.right = Node( 14 ) target = root.left.right printkDistanceNode(root, target, 2 ) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
using System; // C# program to print all nodes at a distance k from given node // A binary tree node public class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right = null ; } } public class BinaryTree { public Node root; /* Recursive function to print all the nodes at distance k in tree (or subtree) rooted with given root. */ public virtual void printkdistanceNodeDown(Node node, int k) { // Base Case if (node == null || k < 0) { return ; } // If we reach a k distant node, print it if (k == 0) { Console.Write(node.data); Console.WriteLine( "" ); return ; } // Recur for left and right subtrees printkdistanceNodeDown(node.left, k - 1); printkdistanceNodeDown(node.right, k - 1); } // Prints all nodes at distance k from a given target node. // The k distant nodes may be upward or downward.This function // Returns distance of root from target node, it returns -1 // if target node is not present in tree rooted with root. public virtual int printkdistanceNode(Node node, Node target, int k) { // Base Case 1: If tree is empty, return -1 if (node == null ) { return -1; } // If target is same as root. Use the downward function // to print all nodes at distance k in subtree rooted with // target or root if (node == target) { printkdistanceNodeDown(node, k); return 0; } // Recur for left subtree int dl = printkdistanceNode(node.left, target, k); // Check if target node was found in left subtree if (dl != -1) { // If root is at distance k from target, print root // Note that dl is Distance of root's left child from // target if (dl + 1 == k) { Console.Write(node.data); Console.WriteLine( "" ); } // Else go to right subtree and print all k-dl-2 distant nodes // Note that the right child is 2 edges away from left child else { printkdistanceNodeDown(node.right, k - dl - 2); } // Add 1 to the distance and return value for parent calls return 1 + dl; } // MIRROR OF ABOVE CODE FOR RIGHT SUBTREE // Note that we reach here only when node was not found in left // subtree int dr = printkdistanceNode(node.right, target, k); if (dr != -1) { if (dr + 1 == k) { Console.Write(node.data); Console.WriteLine( "" ); } else { printkdistanceNodeDown(node.left, k - dr - 2); } return 1 + dr; } // If target was neither present in left nor in right subtree return -1; } // Driver program to test the above functions public static void Main( string [] args) { BinaryTree tree = new BinaryTree(); /* Let us construct the tree shown in above diagram */ tree.root = new Node(20); tree.root.left = new Node(8); tree.root.right = new Node(22); tree.root.left.left = new Node(4); tree.root.left.right = new Node(12); tree.root.left.right.left = new Node(10); tree.root.left.right.right = new Node(14); Node target = tree.root.left.right; tree.printkdistanceNode(tree.root, target, 2); } } // This code is contributed by Shrikant13 |
Javascript
<script> // Javascript program to print all nodes at a distance k from given node // A binary tree node class Node { constructor(item) { this .data = item; this .left = null ; this .right = null ; } } var root = null ; /* Recursive function to print all the nodes at distance k in tree (or subtree) rooted with given root. */ function printkdistanceNodeDown(node, k) { // Base Case if (node == null || k < 0) { return ; } // If we reach a k distant node, print it if (k == 0) { document.write(node.data); document.write( "<br>" ); return ; } // Recur for left and right subtrees printkdistanceNodeDown(node.left, k - 1); printkdistanceNodeDown(node.right, k - 1); } // Prints all nodes at distance k from a given target node. // The k distant nodes may be upward or downward.This function // Returns distance of root from target node, it returns -1 // if target node is not present in tree rooted with root. function printkdistanceNode(node, target, k) { // Base Case 1: If tree is empty, return -1 if (node == null ) { return -1; } // If target is same as root. Use the downward function // to print all nodes at distance k in subtree rooted with // target or root if (node == target) { printkdistanceNodeDown(node, k); return 0; } // Recur for left subtree var dl = printkdistanceNode(node.left, target, k); // Check if target node was found in left subtree if (dl != -1) { // If root is at distance k from target, print root // Note that dl is Distance of root's left child from // target if (dl + 1 == k) { document.write(node.data); document.write( "<br>" ); } // Else go to right subtree and print all k-dl-2 distant nodes // Note that the right child is 2 edges away from left child else { printkdistanceNodeDown(node.right, k - dl - 2); } // Add 1 to the distance and return value for parent calls return 1 + dl; } // MIRROR OF ABOVE CODE FOR RIGHT SUBTREE // Note that we reach here only when node was not found in left // subtree var dr = printkdistanceNode(node.right, target, k); if (dr != -1) { if (dr + 1 == k) { document.write(node.data); document.write( "<br>" ); } else { printkdistanceNodeDown(node.left, k - dr - 2); } return 1 + dr; } // If target was neither present in left nor in right subtree return -1; } // Driver program to test the above functions /* Let us construct the tree shown in above diagram */ root = new Node(20); root.left = new Node(8); root.right = new Node(22); root.left.left = new Node(4); root.left.right = new Node(12); root.left.right.left = new Node(10); root.left.right.right = new Node(14); var target = root.left.right; printkdistanceNode(root, target, 2); // This code is contributed by importantly. </script> |
输出:
420
时间复杂性: 首先,时间复杂度看起来比O(n)大,但如果我们仔细观察,我们可以发现没有节点被遍历超过两次。因此,时间复杂度为O(n)。 本文由 普拉桑特·库马尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
替代解决方案:
- 从根节点获取路径并添加到列表中
- 对于路径中的每个第i个元素,只需迭代并打印(K-i)个距离节点。
JAVA
import java.io.*; import java.util.*; class TreeNode { public int val; public TreeNode left; public TreeNode right; public TreeNode() {} public TreeNode( int val) { this .val = val; } } class GFG { List<TreeNode> path = null ; //Finding all the nodes at a distance K from target //node. public List<Integer> distanceK(TreeNode root, TreeNode target, int K) { path = new ArrayList<>(); findPath(root, target); List<Integer> result = new ArrayList<>(); for ( int i = 0 ; i < path.size(); i++) { findKDistanceFromNode( path.get(i), K - i, result, i == 0 ? null : path.get(i - 1 )); } //Returning list of all nodes at a distance K return result; } // Blocker is used for ancestors node if target at //left then we have to go in right or if target at // right then we have to go in left. public void findKDistanceFromNode(TreeNode node, int dist, List<Integer> result, TreeNode blocker) { if (dist < 0 || node == null || (blocker != null && node == blocker)) { return ; } if (dist == 0 ) { result.add(node.val); } findKDistanceFromNode(node.left, dist - 1 , result, blocker); findKDistanceFromNode(node.right, dist - 1 , result, blocker); } //Finding the path of target node from root node public boolean findPath(TreeNode node, TreeNode target) { if (node == null ) return false ; if (node == target || findPath(node.left, target) || findPath(node.right, target)) { path.add(node); return true ; } return false ; } // Driver program to test the above functions public static void main(String[] args) { GFG gfg = new GFG(); /* Let us construct the tree shown in above diagram */ TreeNode root = new TreeNode( 20 ); root.left = new TreeNode( 8 ); root.right = new TreeNode( 22 ); root.left.left = new TreeNode( 4 ); root.left.right = new TreeNode( 12 ); root.left.right.left = new TreeNode( 10 ); root.left.right.right = new TreeNode( 14 ); TreeNode target = root.left.right; System.out.println(gfg.distanceK(root, target, 2 )); } } |
[4, 20]
时间复杂性: O(n)


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



