旅行商问题（MST近似集）

我们介绍 旅行推销员问题 并讨论了该问题的朴素和动态规划解决方案 以前的职位 这两种解决方案都不可行。事实上，这个问题没有多项式时间解，因为这个问题是一个已知的NP难问题。不过，有一些近似算法可以解决这个问题。只有当问题实例满足三角形不等式时，近似算法才有效。

三角不等式： 从i到达顶点j的最小距离路径总是直接从i到达j，而不是通过其他一些顶点k（或多个顶点），即dis（i，j）总是小于或等于dis（i，k）+dist（k，j）。三角形不等式在许多实际情况下成立。 当代价函数满足三角形不等式时，我们可以设计一个TSP的近似算法，该算法返回一个代价不超过最优旅行代价的两倍的旅行。这个想法是使用 M 最小值 s 淘金 T 稀土元素（MST）。以下是基于MST的算法。

算法： 1) 让1作为销售人员的起点和终点。 2) 使用 普里姆算法 . 3) 列出在构建的MST的预排序遍历中访问的顶点，并在末尾添加1。

让我们考虑下面的例子。第一个图表是给定的图表。第二张图显示了以1作为根构建的MST。MST的前序遍历是1-2-4-3。在最后加1得到1-2-4-3-1，这是该算法的输出。

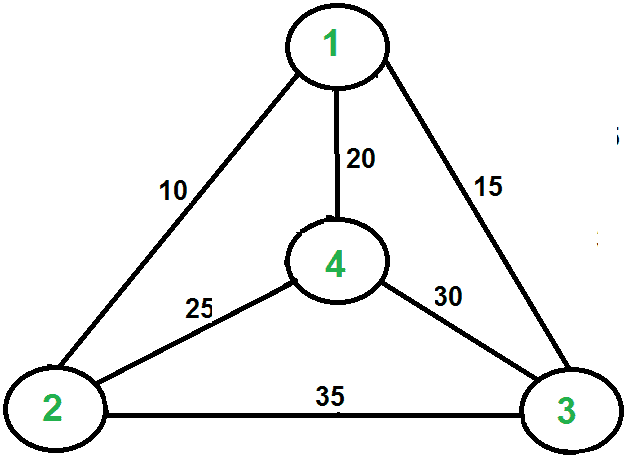
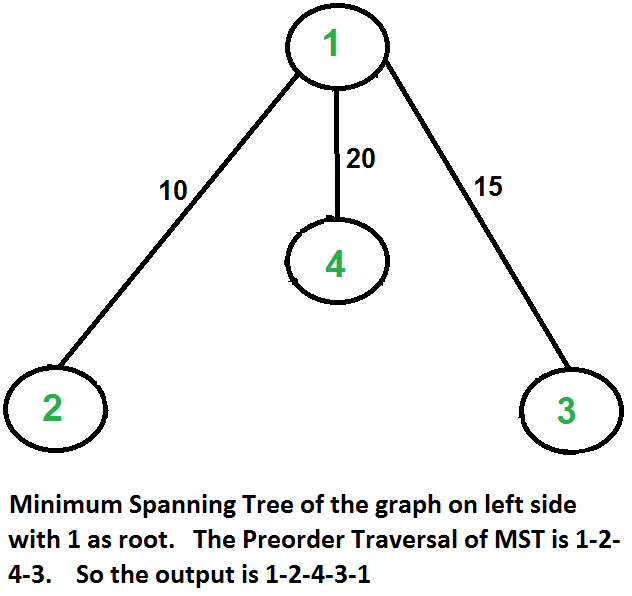在这种情况下，近似算法会产生最优巡更，但它可能不会在所有情况下都产生最优巡更。

这个算法2-近似值是多少？ 上述算法产生的输出成本永远不会超过最佳输出成本的两倍。让我们看看上述算法是如何保证这一点的。 让我们定义一个术语 全程步行 为了理解这一点。“完整漫游”会在以预排序方式首次访问顶点时列出所有顶点，也会在以预排序方式访问子树后返回顶点时列出顶点。上面那棵树的全程是1-2-1-4-1-3-1。 下面是一些重要的事实来证明2-近似性。 1) 最好的旅行推销员旅行的费用永远不会低于MST的费用。（关于 MST 也就是说，它是连接所有顶点的最小成本树）。 2) 全程步行的总成本最多是MST成本的两倍（MST的每一个边缘最多访问两次） 3) 上述算法的输出小于全步行的代价。在上述算法中，我们将预订单行走打印为输出。在预订单漫游中，完整漫游的两条或多条边被替换为一条边。例如，将2-1和1-4替换为1边2-4。如果图遵循三角形不等式，那么这永远是真的。

从以上三个陈述中，我们可以得出结论，近似算法产生的输出成本永远不会超过最佳可能解成本的两倍。

我们讨论了旅行商问题的一个非常简单的2-近似算法。对于这个问题，还有其他更好的近似算法。例如 赫里斯托菲德斯算法 是1.5的近似算法。我们将很快作为单独的帖子讨论这些算法。

参考资料： 算法导论第三版由Clifford Stein、Thomas H.Cormen、Charles E.Leiserson、Ronald L.Rivest编写 http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/aproxagor/TSP/TSP。htm

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论