NP完备性|集1（简介）

我们一直在写解决复杂问题的高效算法，比如 最短路径 , 欧拉图 , 最小生成树 这些都是算法设计者的成功故事。在这篇文章中，我们将讨论计算机科学的失败故事。

所有的计算问题都能用计算机解决吗？ 有些计算问题即使在无限时间内也无法用算法解决。例如，图灵停止问题（给定一个程序和一个输入，程序在使用该输入运行时最终是会停止，还是会永远运行）。Alan Turing证明，对于所有可能的程序输入对，不可能存在一个通用算法来解决暂停问题。证明的一个关键部分是，图灵机被用作计算机和程序的数学定义（源代码） 停顿问题 ). 地位 NP完全 问题是另一个失败故事，NP完全问题是状态未知的问题。尚未发现任何NP完全问题的多项式时间算法，也没有人能够证明其中任何一个问题都不存在多项式时间算法。有趣的是，如果任何一个NP完全问题可以在多项式时间内解决，那么所有的问题都可以解决。

是什么 NP , P , NP完全 和 计算复杂性 问题？ P 是一组可以用确定性图灵机解决的问题 P 多项式时间。

NP 是一组决策问题，可以通过 N 关于确定性图灵机 P 多项式时间。P是NP的子集（任何可以在多项式时间内由确定性机器解决的问题，也可以在多项式时间内由非确定性机器解决）。 非正式地说，NP是一组决策问题，可以通过“幸运算法”（Lucky Algorithm）在多项式时间内解决，这是一种神奇的算法，它总是在给定的一组选择（来源）中做出正确的猜测 参考文献1 ).

NP完全 问题是世界上最难的问题 NP 设置决策问题L是NP完全的，如果： 1) L是NP（NP完全问题的任何给定解都可以快速验证，但没有有效的已知解）。 2) NP中的每一个问题都可以在多项式时间内化简为L（化简定义如下）。

问题是 计算复杂性 如果它遵循上述属性2，则不需要遵循属性1。因此，NP完备集也是NP难集的子集。

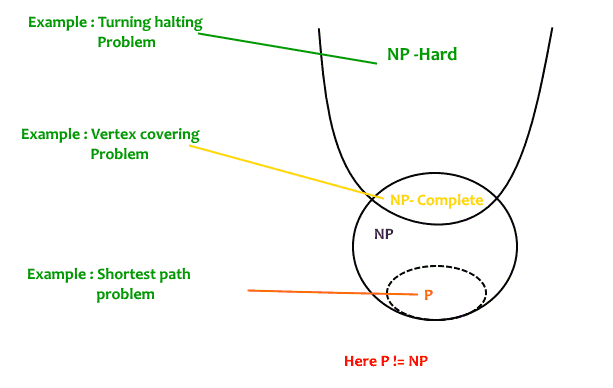
决策与优化问题 NP完全性适用于决策问题领域。之所以这样设置，是因为比较决策问题的难度比比较优化问题的难度更容易。然而，在现实中，能够在多项式时间内解决一个决策问题通常会允许我们在多项式时间内解决相应的优化问题（使用对决策问题的多项式调用次数）。所以，讨论决策问题的难度实际上相当于讨论优化问题的难度。（来源） 参考文献2 ). 例如，考虑 顶点覆盖问题 （给定一个图，找出覆盖所有边的最小顶点集）。这是一个优化问题。相应的决策问题是，给定无向图G和k，是否存在大小为k的顶点覆盖？

什么是减价？ 让我 ₁ 我呢 _2. 这可能是两个决策问题。假设算法A _2. 解决方案L _2. .也就是说，如果y是L的输入 _2. 然后算法A _2. 将根据y是否属于L来回答是或否 _2. 或者不是。 这个想法是从L ₁ 给我 _2. 算法A _2. 可以是算法A的一部分 _1. 解决L _1. .

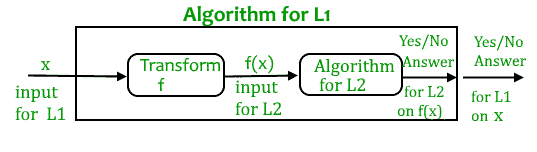
总的来说，减少学习非常重要。例如，如果我们有库函数来解决某些问题，如果我们可以将一个新问题简化为一个已解决的问题，我们可以节省大量时间。考虑一个问题的例子，在这里我们必须找到给定的有向图中的最小乘积路径，其中路径的乘积是沿着路径的边的加权乘法。如果我们有Dijkstra算法的代码来寻找最短路径，我们可以使用所有权重的日志，使用Dijkstra算法来寻找最小乘积路径，而不是为这个新问题编写新的代码。

如何证明一个给定的问题是NP完全问题？ 从NP完全的定义来看，似乎不可能证明问题L是NP完全的。根据定义，它要求我们在多项式时间内证明NP中的每一个问题都可化为L。幸运的是，有另一种方法来证明它。其思想是将一个已知的NP完全问题化简为L。如果多项式时间化简是可能的，我们可以通过化简的传递性证明L是NP完全的（如果一个NP完全问题在多项式时间内可化简为L，那么所有问题在多项式时间内可化简为L）。

第一个被证明是NP完全的问题是什么？ 一定有第一个NP完全问题被NP完全问题的定义所证明。 SAT（布尔可满足性问题） 这是库克证明的第一个NP完全问题（参见CLRS手册）。

即使对工程师来说，了解NP完备性也是很有用的。假设你被要求写一个高效的算法来解决一个对你的公司极其重要的问题。经过很多思考，你只能提出指数时间方法，这是不切实际的。如果你不知道NP完备性，你只能说我没有一个有效的算法。如果你知道NP完全性并证明问题是NP完全的，你可以自豪地说多项式时间解不太可能存在。如果有一个多项式时间解是可能的，那么这个解就解决了许多科学家多年来一直在尝试的计算机科学的一个大问题。

我们将很快讨论更多的NP完全问题及其NP完全性的证明。

参考资料： 麻省理工学院计算复杂性视频讲座 算法导论第三版由Clifford Stein、Thomas H.Cormen、Charles E.Leiserson、Ronald L.Rivest编写 http://www.ics.uci.edu/~eppstein/161/960312。html

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论