我们已经讨论了这个问题 水平顺序遍历 前一篇文章中的一篇文章。我们的想法是先打印最后一级,然后打印最后一级,依此类推。像级别顺序遍历一样,每个级别都从左到右打印。
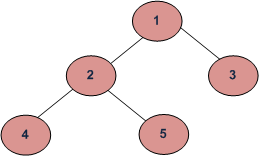
上述树的反向水平顺序遍历为“4 5 2 3 1”。 这两种方法都适用于 正常水平顺序遍历 可以很容易地进行修改,以执行反向级别顺序遍历。
方法1(打印给定级别的递归函数) 我们可以很容易地修改方法1的正常 水平顺序遍历 .在方法1中,我们有一个方法printGivenLevel(),它打印给定的级别号。我们唯一需要改变的是,我们不是从第一级调用printGivenLevel()到最后一级,而是从最后一级调用它到第一级。
C++
// A recursive C++ program to print // REVERSE level order traversal #include <bits/stdc++.h> using namespace std; /* A binary tree node has data, pointer to left and right child */ class node { public : int data; node* left; node* right; }; /*Function prototypes*/ void printGivenLevel(node* root, int level); int height(node* node); node* newNode( int data); /* Function to print REVERSE level order traversal a tree*/ void reverseLevelOrder(node* root) { int h = height(root); int i; for (i=h; i>=1; i--) //THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER printGivenLevel(root, i); } /* Print nodes at a given level */ void printGivenLevel(node* root, int level) { if (root == NULL) return ; if (level == 1) cout << root->data << " " ; else if (level > 1) { printGivenLevel(root->left, level - 1); printGivenLevel(root->right, level - 1); } } /* Compute the "height" of a tree -- the number of nodes along the longest path from the root node down to the farthest leaf node.*/ int height(node* node) { if (node == NULL) return 0; else { /* compute the height of each subtree */ int lheight = height(node->left); int rheight = height(node->right); /* use the larger one */ if (lheight > rheight) return (lheight + 1); else return (rheight + 1); } } /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ node* newNode( int data) { node* Node = new node(); Node->data = data; Node->left = NULL; Node->right = NULL; return (Node); } /* Driver code*/ int main() { node *root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout << "Level Order traversal of binary tree is " ; reverseLevelOrder(root); return 0; } // This code is contributed by rathbhupendra |
C
// A recursive C program to print REVERSE level order traversal #include <stdio.h> #include <stdlib.h> /* A binary tree node has data, pointer to left and right child */ struct node { int data; struct node* left; struct node* right; }; /*Function prototypes*/ void printGivenLevel( struct node* root, int level); int height( struct node* node); struct node* newNode( int data); /* Function to print REVERSE level order traversal a tree*/ void reverseLevelOrder( struct node* root) { int h = height(root); int i; for (i=h; i>=1; i--) //THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER printGivenLevel(root, i); } /* Print nodes at a given level */ void printGivenLevel( struct node* root, int level) { if (root == NULL) return ; if (level == 1) printf ( "%d " , root->data); else if (level > 1) { printGivenLevel(root->left, level-1); printGivenLevel(root->right, level-1); } } /* Compute the "height" of a tree -- the number of nodes along the longest path from the root node down to the farthest leaf node.*/ int height( struct node* node) { if (node==NULL) return 0; else { /* compute the height of each subtree */ int lheight = height(node->left); int rheight = height(node->right); /* use the larger one */ if (lheight > rheight) return (lheight+1); else return (rheight+1); } } /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newNode( int data) { struct node* node = ( struct node*) malloc ( sizeof ( struct node)); node->data = data; node->left = NULL; node->right = NULL; return (node); } /* Driver program to test above functions*/ int main() { struct node *root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); printf ( "Level Order traversal of binary tree is " ); reverseLevelOrder(root); return 0; } |
JAVA
// A recursive java program to print reverse level order traversal // A binary tree node class Node { int data; Node left, right; Node( int item) { data = item; left = right; } } class BinaryTree { Node root; /* Function to print REVERSE level order traversal a tree*/ void reverseLevelOrder(Node node) { int h = height(node); int i; for (i = h; i >= 1 ; i--) //THE ONLY LINE DIFFERENT FROM NORMAL LEVEL ORDER { printGivenLevel(node, i); } } /* Print nodes at a given level */ void printGivenLevel(Node node, int level) { if (node == null ) return ; if (level == 1 ) System.out.print(node.data + " " ); else if (level > 1 ) { printGivenLevel(node.left, level - 1 ); printGivenLevel(node.right, level - 1 ); } } /* Compute the "height" of a tree -- the number of nodes along the longest path from the root node down to the farthest leaf node.*/ int height(Node node) { if (node == null ) return 0 ; else { /* compute the height of each subtree */ int lheight = height(node.left); int rheight = height(node.right); /* use the larger one */ if (lheight > rheight) return (lheight + 1 ); else return (rheight + 1 ); } } // Driver program to test above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); // Let us create trees shown in above diagram tree.root = new Node( 1 ); tree.root.left = new Node( 2 ); tree.root.right = new Node( 3 ); tree.root.left.left = new Node( 4 ); tree.root.left.right = new Node( 5 ); System.out.println( "Level Order traversal of binary tree is : " ); tree.reverseLevelOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal |
python
# A recursive Python program to print REVERSE level order traversal # A binary tree node class Node: # Constructor to create a new node def __init__( self , data): self .data = data self .left = None self .right = None # Function to print reverse level order traversal def reverseLevelOrder(root): h = height(root) for i in reversed ( range ( 1 , h + 1 )): printGivenLevel(root,i) # Print nodes at a given level def printGivenLevel(root, level): if root is None : return if level = = 1 : print root.data, elif level> 1 : printGivenLevel(root.left, level - 1 ) printGivenLevel(root.right, level - 1 ) # Compute the height of a tree-- the number of # nodes along the longest path from the root node # down to the farthest leaf node def height(node): if node is None : return 0 else : # Compute the height of each subtree lheight = height(node.left) rheight = height(node.right) # Use the larger one if lheight > rheight : return lheight + 1 else : return rheight + 1 # Driver program to test above function root = Node( 1 ) root.left = Node( 2 ) root.right = Node( 3 ) root.left.left = Node( 4 ) root.left.right = Node( 5 ) print "Level Order traversal of binary tree is" reverseLevelOrder(root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
// A recursive C# program to print // reverse level order traversal using System; // A binary tree node class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right; } } class BinaryTree { Node root; /* Function to print REVERSE level order traversal a tree*/ void reverseLevelOrder(Node node) { int h = height(node); int i; for (i = h; i >= 1; i--) // THE ONLY LINE DIFFERENT // FROM NORMAL LEVEL ORDER { printGivenLevel(node, i); } } /* Print nodes at a given level */ void printGivenLevel(Node node, int level) { if (node == null ) return ; if (level == 1) Console.Write(node.data + " " ); else if (level > 1) { printGivenLevel(node.left, level - 1); printGivenLevel(node.right, level - 1); } } /* Compute the "height" of a tree -- the number of nodes along the longest path from the root node down to the farthest leaf node.*/ int height(Node node) { if (node == null ) return 0; else { /* compute the height of each subtree */ int lheight = height(node.left); int rheight = height(node.right); /* use the larger one */ if (lheight > rheight) return (lheight + 1); else return (rheight + 1); } } // Driver Code static public void Main(String []args) { BinaryTree tree = new BinaryTree(); // Let us create trees shown // in above diagram tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); Console.WriteLine( "Level Order traversal " + "of binary tree is : " ); tree.reverseLevelOrder(tree.root); } } // This code is contributed // by Arnab Kundu |
Javascript
<script> // A recursive JavaScript program to print // reverse level order traversal // A binary tree node class Node { constructor(item) { this .data = item; this .left = null ; this .right = null ; } } class BinaryTree { constructor() { this .root = null ; } /* Function to print REVERSE level order traversal a tree*/ reverseLevelOrder(node) { var h = this .height(node); var i; for ( i = h; i >= 1; i-- // THE ONLY LINE DIFFERENT // FROM NORMAL LEVEL ORDER ) { this .printGivenLevel(node, i); } } /* Print nodes at a given level */ printGivenLevel(node, level) { if (node == null ) return ; if (level == 1) document.write(node.data + " " ); else if (level > 1) { this .printGivenLevel(node.left, level - 1); this .printGivenLevel(node.right, level - 1); } } /* Compute the "height" of a tree -- the number of nodes along the longest path from the root node down to the farthest leaf node.*/ height(node) { if (node == null ) return 0; else { /* compute the height of each subtree */ var lheight = this .height(node.left); var rheight = this .height(node.right); /* use the larger one */ if (lheight > rheight) return lheight + 1; else return rheight + 1; } } } // Driver Code var tree = new BinaryTree(); // Let us create trees shown // in above diagram tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); document.write( "Level Order traversal " + "of binary tree is : <br>" ); tree.reverseLevelOrder(tree.root); </script> |
输出:
Level Order traversal of binary tree is4 5 2 3 1
时间复杂性: 该方法最坏情况下的时间复杂度为O(n^2)。对于倾斜树,printGivenLevel()需要O(n)个时间,其中n是倾斜树中的节点数。所以printLevelOrder()的时间复杂度是O(n)+O(n-1)+O(n-2)+O(1)是O(n^2)。 方法2(使用队列和堆栈) 方法2 正常水平顺序遍历 也可以很容易地修改为按相反顺序打印级别顺序遍历。其想法是使用deque(双端队列)来获得反向级别的顺序。deque允许在两端插入和删除。如果我们执行普通的级别顺序遍历,而不是打印节点,将节点推到堆栈中,然后打印deque的内容,我们会得到上面示例树的“5 4 3 2 1”,但输出应该是“4 5 2 3 1”。为了得到正确的序列(从左到右,每一级),我们以相反的顺序处理一个节点的子节点,我们首先将右子树推到deque,然后处理左子树。
C++
// A C++ program to print REVERSE level order traversal using stack and queue // This approach is adopted from following link #include <bits/stdc++.h> using namespace std; /* A binary tree node has data, pointer to left and right children */ struct node { int data; struct node* left; struct node* right; }; /* Given a binary tree, print its nodes in reverse level order */ void reverseLevelOrder(node* root) { stack <node *> S; queue <node *> Q; Q.push(root); // Do something like normal level order traversal order. Following are the // differences with normal level order traversal // 1) Instead of printing a node, we push the node to stack // 2) Right subtree is visited before left subtree while (Q.empty() == false ) { /* Dequeue node and make it root */ root = Q.front(); Q.pop(); S.push(root); /* Enqueue right child */ if (root->right) Q.push(root->right); // NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT /* Enqueue left child */ if (root->left) Q.push(root->left); } // Now pop all items from stack one by one and print them while (S.empty() == false ) { root = S.top(); cout << root->data << " " ; S.pop(); } } /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ node* newNode( int data) { node* temp = new node; temp->data = data; temp->left = NULL; temp->right = NULL; return (temp); } /* Driver program to test above functions*/ int main() { struct node *root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); root->right->left = newNode(6); root->right->right = newNode(7); cout << "Level Order traversal of binary tree is " ; reverseLevelOrder(root); return 0; } |
JAVA
// A recursive java program to print reverse level order traversal // using stack and queue import java.util.LinkedList; import java.util.Queue; import java.util.Stack; /* A binary tree node has data, pointer to left and right children */ class Node { int data; Node left, right; Node( int item) { data = item; left = right; } } class BinaryTree { Node root; /* Given a binary tree, print its nodes in reverse level order */ void reverseLevelOrder(Node node) { Stack<Node> S = new Stack(); Queue<Node> Q = new LinkedList(); Q.add(node); // Do something like normal level order traversal order.Following // are the differences with normal level order traversal // 1) Instead of printing a node, we push the node to stack // 2) Right subtree is visited before left subtree while (Q.isEmpty() == false ) { /* Dequeue node and make it root */ node = Q.peek(); Q.remove(); S.push(node); /* Enqueue right child */ if (node.right != null ) // NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT Q.add(node.right); /* Enqueue left child */ if (node.left != null ) Q.add(node.left); } // Now pop all items from stack one by one and print them while (S.empty() == false ) { node = S.peek(); System.out.print(node.data + " " ); S.pop(); } } // Driver program to test above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); // Let us create trees shown in above diagram tree.root = new Node( 1 ); tree.root.left = new Node( 2 ); tree.root.right = new Node( 3 ); tree.root.left.left = new Node( 4 ); tree.root.left.right = new Node( 5 ); tree.root.right.left = new Node( 6 ); tree.root.right.right = new Node( 7 ); System.out.println( "Level Order traversal of binary tree is :" ); tree.reverseLevelOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal |
python
# Python program to print REVERSE level order traversal using # stack and queue from collections import deque # A binary tree node class Node: # Constructor to create a new node def __init__( self , data): self .data = data self .left = None self .right = None # Given a binary tree, print its nodes in reverse level order def reverseLevelOrder(root): # we can use a double ended queue which provides O(1) insert at the beginning # using the appendleft method # we do the regular level order traversal but instead of processing the # left child first we process the right child first and the we process the left child # of the current Node # we can do this One pass reduce the space usage not in terms of complexity but intuitively q = deque() q.append(root) ans = deque() while q: node = q.popleft() if node is None : continue ans.appendleft(node.data) if node.right: q.append(node.right) if node.left: q.append(node.left) return ans # Driver program to test above function root = Node( 1 ) root.left = Node( 2 ) root.right = Node( 3 ) root.left.left = Node( 4 ) root.left.right = Node( 5 ) root.right.left = Node( 6 ) root.right.right = Node( 7 ) print "Level Order traversal of binary tree is" reverseLevelOrder(root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
// A recursive C# program to print reverse // level order traversal using stack and queue using System.Collections.Generic; using System; /* A binary tree node has data, pointer to left and right children */ public class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right; } } public class BinaryTree { Node root; /* Given a binary tree, print its nodes in reverse level order */ void reverseLevelOrder(Node node) { Stack<Node> S = new Stack<Node>(); Queue<Node> Q = new Queue<Node>(); Q.Enqueue(node); // Do something like normal level // order traversal order.Following // are the differences with normal // level order traversal // 1) Instead of printing a node, we push the node to stack // 2) Right subtree is visited before left subtree while (Q.Count>0) { /* Dequeue node and make it root */ node = Q.Peek(); Q.Dequeue(); S.Push(node); /* Enqueue right child */ if (node.right != null ) // NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT Q.Enqueue(node.right); /* Enqueue left child */ if (node.left != null ) Q.Enqueue(node.left); } // Now pop all items from stack // one by one and print them while (S.Count>0) { node = S.Peek(); Console.Write(node.data + " " ); S.Pop(); } } // Driver code public static void Main() { BinaryTree tree = new BinaryTree(); // Let us create trees shown in above diagram tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); tree.root.right.left = new Node(6); tree.root.right.right = new Node(7); Console.WriteLine( "Level Order traversal of binary tree is :" ); tree.reverseLevelOrder(tree.root); } } /* This code contributed by PrinciRaj1992 */ |
Javascript
<script> // A recursive javascript program to print // reverse level order traversal // using stack and queue /* A binary tree node has data, pointer to left and right children */ class Node { constructor(item) { this .data = item; this .left = this .right= null ; } } let root; /* Given a binary tree, print its nodes in reverse level order */ function reverseLevelOrder(node) { let S = []; let Q = []; Q.push(node); // Do something like normal // level order traversal order.Following // are the differences with normal // level order traversal // 1) Instead of printing a node, // we push the node to stack // 2) Right subtree is visited before left subtree while (Q.length != 0) { /* Dequeue node and make it root */ node = Q[0]; Q.shift(); S.push(node); /* Enqueue right child */ if (node.right != null ) // NOTE: RIGHT CHILD IS ENQUEUED BEFORE LEFT Q.push(node.right); /* Enqueue left child */ if (node.left != null ) Q.push(node.left); } // Now pop all items from stack // one by one and print them while (S.length != 0) { node = S.pop(); document.write(node.data + " " ); } } // Driver program to test above functions // Let us create trees shown in above diagram root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7); document.write( "Level Order traversal of binary tree is :<br>" ); reverseLevelOrder(root); // This code is contributed by avanitrachhadiya2155 </script> |
输出:
Level Order traversal of binary tree is4 5 6 7 2 3 1
时间复杂性: O(n),其中n是二叉树中的节点数。
?list=PLqM7alHXFySHCXD7r1J0ky9Zg_GBB1dbk
如果您在上述程序/算法或其他解决相同问题的方法中发现任何缺陷,请写评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



