给我一条短信 txt[0..n-1] 还有一种模式 帕特[0..m-1] ,编写一个函数 搜索(字符pat[],字符txt[] 打印所有出现的 帕特[] 在里面 txt[] .你可以假设n>m。 例如:
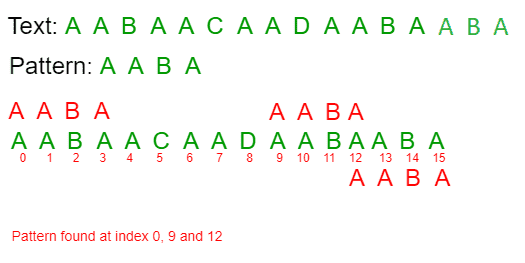
Input: txt[] = "THIS IS A TEST TEXT" pat[] = "TEST"Output: Pattern found at index 10Input: txt[] = "AABAACAADAABAABA" pat[] = "AABA"Output: Pattern found at index 0 Pattern found at index 9 Pattern found at index 12
模式搜索是计算机科学中的一个重要问题。当我们在记事本/word文件、浏览器或数据库中搜索字符串时,会使用模式搜索算法来显示搜索结果。 我们在之前的帖子中讨论了以下算法: 朴素算法 KMP算法 拉宾-卡普算法 在这篇文章中,我们将讨论基于有限自动机(FA)的模式搜索算法。在基于FA的算法中,我们对模式进行预处理,并构建一个表示有限自动机的2D数组。FA的构造是该算法的主要难点。一旦构建了FA,搜索就很简单了。在搜索中,我们只需要从自动机的第一个状态和文本的第一个字符开始。在每一步中,我们考虑文本的下一个字符,寻找生成的FA中的下一个状态并移动到一个新的状态。如果我们达到最后的状态,那么模式就会在文本中找到。搜索过程的时间复杂度为O(n)。 在讨论FA构造之前,让我们先看看下面的模式ACACAGA的FA。


以上图表表示模式ACACAGA的图形和表格表示。 FA中的状态数为M+1,其中M是图案的长度。构造FA的主要任务是从每个可能的角色的当前状态中获取下一个状态。给定一个字符x和一个状态k,我们可以通过考虑字符串“pat[0..k-1]x”来获得下一个状态,该字符串基本上是模式字符pat[0]、pat[1]…pat[k-1]和字符x的串联。其思想是获得给定模式的最长前缀的长度,这样前缀也是“pat[0..k-1]x”的后缀。长度的值给出了下一个状态。例如,让我们看看如何从上图中的当前状态5和字符“C”中获取下一个状态。我们需要考虑字符串“PAT(0…4)C”,它是“Acac”。图案最长前缀的长度,即前缀为“ACACAC”的后缀为4(“ACAC”)。所以下一个状态(来自状态5)是字符“C”的4。 在下面的代码中,computeTF()构造FA。computeTF()的时间复杂度为O(m^3*无字符数),其中m是模式的长度,无字符数是字母表的大小(模式和文本中可能的字符总数)。该实现尝试所有可能的前缀,从最长的后缀“pat[0..k-1]x”开始。有更好的实现可以在O(m*NO_OF_CHARS)中构造FA(提示:我们可以使用 KMP算法中lps阵列的构造 ).我们已将更好的实施纳入 下一篇关于模式搜索的帖子 .
C
// C program for Finite Automata Pattern searching // Algorithm #include<stdio.h> #include<string.h> #define NO_OF_CHARS 256 int getNextState( char *pat, int M, int state, int x) { // If the character c is same as next character // in pattern,then simply increment state if (state < M && x == pat[state]) return state+1; // ns stores the result which is next state int ns, i; // ns finally contains the longest prefix // which is also suffix in "pat[0..state-1]c" // Start from the largest possible value // and stop when you find a prefix which // is also suffix for (ns = state; ns > 0; ns--) { if (pat[ns-1] == x) { for (i = 0; i < ns-1; i++) if (pat[i] != pat[state-ns+1+i]) break ; if (i == ns-1) return ns; } } return 0; } /* This function builds the TF table which represents4 Finite Automata for a given pattern */ void computeTF( char *pat, int M, int TF[][NO_OF_CHARS]) { int state, x; for (state = 0; state <= M; ++state) for (x = 0; x < NO_OF_CHARS; ++x) TF[state][x] = getNextState(pat, M, state, x); } /* Prints all occurrences of pat in txt */ void search( char *pat, char *txt) { int M = strlen (pat); int N = strlen (txt); int TF[M+1][NO_OF_CHARS]; computeTF(pat, M, TF); // Process txt over FA. int i, state=0; for (i = 0; i < N; i++) { state = TF[state][txt[i]]; if (state == M) printf ( " Pattern found at index %d" , i-M+1); } } // Driver program to test above function int main() { char *txt = "AABAACAADAABAAABAA" ; char *pat = "AABA" ; search(pat, txt); return 0; } |
CPP
// CPP program for Finite Automata Pattern searching // Algorithm #include <bits/stdc++.h> using namespace std; #define NO_OF_CHARS 256 int getNextState(string pat, int M, int state, int x) { // If the character c is same as next character // in pattern,then simply increment state if (state < M && x == pat[state]) return state+1; // ns stores the result which is next state int ns, i; // ns finally contains the longest prefix // which is also suffix in "pat[0..state-1]c" // Start from the largest possible value // and stop when you find a prefix which // is also suffix for (ns = state; ns > 0; ns--) { if (pat[ns-1] == x) { for (i = 0; i < ns-1; i++) if (pat[i] != pat[state-ns+1+i]) break ; if (i == ns-1) return ns; } } return 0; } /* This function builds the TF table which represents4 Finite Automata for a given pattern */ void computeTF(string pat, int M, int TF[][NO_OF_CHARS]) { int state, x; for (state = 0; state <= M; ++state) for (x = 0; x < NO_OF_CHARS; ++x) TF[state][x] = getNextState(pat, M, state, x); } /* Prints all occurrences of pat in txt */ void search(string pat, string txt) { int M = pat.size(); int N = txt.size(); int TF[M+1][NO_OF_CHARS]; computeTF(pat, M, TF); // Process txt over FA. int i, state=0; for (i = 0; i < N; i++) { state = TF[state][txt[i]]; if (state == M) cout<< " Pattern found at index " << i-M+1<<endl; } } // Driver program to test above function int main() { string txt = "AABAACAADAABAAABAA" ; string pat = "AABA" ; search(pat, txt); return 0; } //This code is contributed by rathbhupendra |
JAVA
// Java program for Finite Automata Pattern // searching Algorithm class GFG { static int NO_OF_CHARS = 256 ; static int getNextState( char [] pat, int M, int state, int x) { // If the character c is same as next // character in pattern,then simply // increment state if (state < M && x == pat[state]) return state + 1 ; // ns stores the result which is next state int ns, i; // ns finally contains the longest prefix // which is also suffix in "pat[0..state-1]c" // Start from the largest possible value // and stop when you find a prefix which // is also suffix for (ns = state; ns > 0 ; ns--) { if (pat[ns- 1 ] == x) { for (i = 0 ; i < ns- 1 ; i++) if (pat[i] != pat[state-ns+ 1 +i]) break ; if (i == ns- 1 ) return ns; } } return 0 ; } /* This function builds the TF table which represents Finite Automata for a given pattern */ static void computeTF( char [] pat, int M, int TF[][]) { int state, x; for (state = 0 ; state <= M; ++state) for (x = 0 ; x < NO_OF_CHARS; ++x) TF[state][x] = getNextState(pat, M, state, x); } /* Prints all occurrences of pat in txt */ static void search( char [] pat, char [] txt) { int M = pat.length; int N = txt.length; int [][] TF = new int [M+ 1 ][NO_OF_CHARS]; computeTF(pat, M, TF); // Process txt over FA. int i, state = 0 ; for (i = 0 ; i < N; i++) { state = TF[state][txt[i]]; if (state == M) System.out.println( "Pattern found " + "at index " + (i-M+ 1 )); } } // Driver code public static void main(String[] args) { char [] pat = "AABAACAADAABAAABAA" .toCharArray(); char [] txt = "AABA" .toCharArray(); search(txt,pat); } } // This code is contributed by debjitdbb. |
Python3
# Python program for Finite Automata # Pattern searching Algorithm NO_OF_CHARS = 256 def getNextState(pat, M, state, x): ''' calculate the next state ''' # If the character c is same as next character # in pattern, then simply increment state if state < M and x = = ord (pat[state]): return state + 1 i = 0 # ns stores the result which is next state # ns finally contains the longest prefix # which is also suffix in "pat[0..state-1]c" # Start from the largest possible value and # stop when you find a prefix which is also suffix for ns in range (state, 0 , - 1 ): if ord (pat[ns - 1 ]) = = x: while (i<ns - 1 ): if pat[i] ! = pat[state - ns + 1 + i]: break i + = 1 if i = = ns - 1 : return ns return 0 def computeTF(pat, M): ''' This function builds the TF table which represents Finite Automata for a given pattern ''' global NO_OF_CHARS TF = [[ 0 for i in range (NO_OF_CHARS)] for _ in range (M + 1 )] for state in range (M + 1 ): for x in range (NO_OF_CHARS): z = getNextState(pat, M, state, x) TF[state][x] = z return TF def search(pat, txt): ''' Prints all occurrences of pat in txt ''' global NO_OF_CHARS M = len (pat) N = len (txt) TF = computeTF(pat, M) # Process txt over FA. state = 0 for i in range (N): state = TF[state][ ord (txt[i])] if state = = M: print ( "Pattern found at index: {}" . format (i - M + 1 )) # Driver program to test above function def main(): txt = "AABAACAADAABAAABAA" pat = "AABA" search(pat, txt) if __name__ = = '__main__' : main() # This code is contributed by Atul Kumar |
C#
// C# program for Finite Automata Pattern // searching Algorithm using System; class GFG { public static int NO_OF_CHARS = 256; public static int getNextState( char [] pat, int M, int state, int x) { // If the character c is same as next // character in pattern,then simply // increment state if (state < M && ( char )x == pat[state]) { return state + 1; } // ns stores the result // which is next state int ns, i; // ns finally contains the longest // prefix which is also suffix in // "pat[0..state-1]c" // Start from the largest possible // value and stop when you find a // prefix which is also suffix for (ns = state; ns > 0; ns--) { if (pat[ns - 1] == ( char )x) { for (i = 0; i < ns - 1; i++) { if (pat[i] != pat[state - ns + 1 + i]) { break ; } } if (i == ns - 1) { return ns; } } } return 0; } /* This function builds the TF table which represents Finite Automata for a given pattern */ public static void computeTF( char [] pat, int M, int [][] TF) { int state, x; for (state = 0; state <= M; ++state) { for (x = 0; x < NO_OF_CHARS; ++x) { TF[state][x] = getNextState(pat, M, state, x); } } } /* Prints all occurrences of pat in txt */ public static void search( char [] pat, char [] txt) { int M = pat.Length; int N = txt.Length; int [][] TF = RectangularArrays.ReturnRectangularIntArray(M + 1, NO_OF_CHARS); computeTF(pat, M, TF); // Process txt over FA. int i, state = 0; for (i = 0; i < N; i++) { state = TF[state][txt[i]]; if (state == M) { Console.WriteLine( "Pattern found " + "at index " + (i - M + 1)); } } } public static class RectangularArrays { public static int [][] ReturnRectangularIntArray( int size1, int size2) { int [][] newArray = new int [size1][]; for ( int array1 = 0; array1 < size1; array1++) { newArray[array1] = new int [size2]; } return newArray; } } // Driver code public static void Main( string [] args) { char [] pat = "AABAACAADAABAAABAA" .ToCharArray(); char [] txt = "AABA" .ToCharArray(); search(txt,pat); } } // This code is contributed by Shrikant13 |
Javascript
<script> // Javascript program for Finite Automata Pattern // searching Algorithm let NO_OF_CHARS = 256; function getNextState(pat,M,state,x) { // If the character c is same as next // character in pattern,then simply // increment state if (state < M && x == pat[state].charCodeAt(0)) return state + 1; // ns stores the result which is next state let ns, i; // ns finally contains the longest prefix // which is also suffix in "pat[0..state-1]c" // Start from the largest possible value // and stop when you find a prefix which // is also suffix for (ns = state; ns > 0; ns--) { if (pat[ns-1].charCodeAt(0) == x) { for (i = 0; i < ns-1; i++) if (pat[i] != pat[state-ns+1+i]) break ; if (i == ns-1) return ns; } } return 0; } /* This function builds the TF table which represents Finite Automata for a given pattern */ function computeTF(pat,M,TF) { let state, x; for (state = 0; state <= M; ++state) for (x = 0; x < NO_OF_CHARS; ++x) TF[state][x] = getNextState(pat, M, state, x); } /* Prints all occurrences of pat in txt */ function search(pat,txt) { let M = pat.length; let N = txt.length; let TF = new Array(M+1); for (let i=0;i<M+1;i++) { TF[i]= new Array(NO_OF_CHARS); for (let j=0;j<NO_OF_CHARS;j++) TF[i][j]=0; } computeTF(pat, M, TF); // Process txt over FA. let i, state = 0; for (i = 0; i < N; i++) { state = TF[state][txt[i].charCodeAt(0)]; if (state == M) document.write( "Pattern found " + "at index " + (i-M+1)+ "<br>" ); } } // Driver code let pat = "AABAACAADAABAAABAA" .split( "" ); let txt = "AABA" .split( "" ); search(txt,pat); // This code is contributed by avanitrachhadiya2155 </script> |
输出:
Pattern found at index 0 Pattern found at index 9 Pattern found at index 13
参考资料: 托马斯·H·科曼、查尔斯·E·莱瑟森、罗纳德·L·里维斯特、克利福德·斯坦的算法简介 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



