竞赛树（赢家树）和二进制堆

给定一个由N名球员组成的团队。最少需要多少场比赛才能找到第二好的选手？

我们可以使用基于竞赛树（二进制堆）的对手参数。

竞赛树 是最小（最大）堆的一种形式，它是一个完整的二叉树。每个外部节点代表一个玩家，内部节点代表赢家。在竞赛树中，每个内部节点包含赢家，每个叶节点包含一名玩家。

二叉树中有N–1个内部节点和N个叶（外部）节点。有关详细信息，请参阅 这篇帖子 （将n=2放入帖子给出的等式中）。

很明显，要在N个玩家中选择最好的玩家，（N-1）个被淘汰的玩家，即我们需要最少（N-1）个游戏（比较）。从数学上我们可以证明这一点。在二叉树中，I=E–1，其中I是内部节点数，E是外部节点数。这意味着要找到数组的最大或最小元素，我们需要N–1（内部节点）比较。

亚军

最佳球员选择过程中探索的信息可用于在追踪下一个最佳球员时最小化比较次数。例如，我们可以在比赛中挑选第二好的球员 （N+log） _2. N–2） 比较。

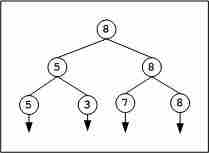
下图显示了一个锦标赛树( 赢家树 )作为一个最大的堆。请注意 败者树 这是不同的。

上面的树包含4个叶节点，代表玩家，有3个级别0、1和2。最初，2场比赛在2级进行，一场在5到3级之间，另一场在7到8级之间。在下一步中，在5点到8点之间再进行一场比赛，以确定最终的赢家。总的来说，我们需要3个比较。对于第二名选手，我们需要追踪最终获胜者的候选人，这导致第二名为7名。

排序数组的中值

竞赛树可以有效地用于寻找排序数组的中值。假设给定M个大小相等的排序数组（为简单起见）。我们可以将所有这些排序的数组附加到锦标赛树，每个叶子一个数组。我们需要一棵高的树 CEIL（原木） _2. M） 至少有M个外部节点。

考虑一个例子。给定3个（M=3）最大大小为5个元素的排序整数数组。

{ 2, 5, 7, 11, 15 } ---- Array1
{1, 3, 4} ---- Array2
{6, 8, 12, 13, 14} ---- Array3

比赛树的高度应该是多少？我们需要构建一个高度为log的竞赛树 _2. 3 .= 1.585=2四舍五入到下一个整数。高度为2的二叉树将有4片叶子，我们可以在上面附加数组，如下图所示。

第一场比赛结束后，这棵树如下图所示，

我们可以看到获胜者来自Array2。因此，Array2的下一个元素将潜入，游戏将沿着上一届锦标赛的赢家路线进行。

请注意，无穷大用作哨兵元素。根据节点中保存的数据，我们可以选择哨兵角色。例如，我们通常将指针存储在节点而不是键中，因此NULL可以充当哨兵。如果任何阵列耗尽，我们将用哨兵填充相应的叶子和即将到来的内部节点。

第二场比赛结束后，树如下图所示，

下一个赢家来自Array1，所以Array1阵列的下一个元素是5，将进入下一轮，下一场比赛将沿着2的路径进行。

比赛可以继续进行，直到我们得到中间元素（5+3+5）/2=7。请注意，有更好的算法可以找到排序数组并集的中值，有关详细信息，请参阅下面给出的相关链接。

通常情况下，M个大小为L的排序列表 _1. L ₂ …我 _M 需要时间复杂性 （L） _1. +L _2. +…+L _m )*logM） 合并所有数组，然后 O（m*logM） 是时候找到中位数了，在哪里 M 是中间位置。

从十亿个未排序的元素中选择最小的一百万个元素：

作为一个简单的解决方案，我们可以对10亿个数字进行排序，然后选择前100万个。

在一个有限的内存系统中，排序十亿个元素并挑选前一百万个元素似乎是不切实际的。我们可以使用锦标赛树方法。在任何时候，只有树的元素才能被存储在内存中。

将大数组（可能存储在磁盘上）拆分为大小为100万的较小数组（甚至可以由机器排序的更小数组）。对这1000个小尺寸阵列进行排序，并将它们作为单个文件存储在磁盘上。构建一棵竞赛树，它至少可以有1000个叶节点（树的高度为10，从2开始） ⁹ 10 ，如果单个文件的大小更小，我们将需要更多的叶节点）。每个叶节点都有一个引擎，可以从存储在磁盘上的已排序文件中选择下一个元素。我们可以玩锦标赛树游戏来提取前100万个元素。

总成本=整理1000张100万张的列表+树结构+锦标赛

实施 我们需要以自下而上的方式建造这棵树。所有的叶节点首先被填满。从树的左端开始，沿宽度填充（即从2 ^k-1 到2 ^K –1，其中k是树的深度）并玩游戏。在用很少的例子练习之后，编写代码就很容易了。实现在下面的代码中讨论

使用最小比较的第二最小元素

相关职位 查找数组中的最小和第二小元素 . 使用最小比较的第二最小元素

-由 文基 。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请发表评论。