加泰罗尼亚数的应用-yiteyi-C++库

null

背景： 加泰罗尼亚数字 $C_{n} = (2n)!/(n+1)!n! = prod^{n}_{k=2} frac{n+k}{k} for_ n >= 0$ $C_{0} = 1 C_{n+1} = sum ^{n} _{i=0} C_{i}C_{n-i} for_ n>=0$ 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …

参考这用于实施n’th Catalan编号。

应用：

具有n个键的可能二叉搜索树的数目 .
包含n对正确匹配的括号的表达式数。对于n=3，可能的表达式是（（（）），（（）），（（）），（（）），（（）），（（）），（（））。
n+2边的凸多边形通过连接顶点可以拆分为三角形的方式的数量。
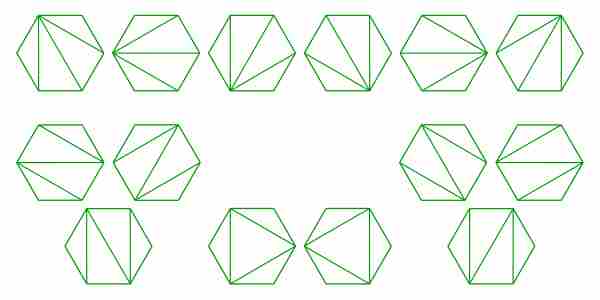
数量全二叉树（如果每个顶点有两个子树或没有子树，则有根二叉树是满的）有n+1片叶子。
不同的未标记二叉树的数量可以有n个节点 .
矩形网格上从左下角（即（n-1，0）到右上角（0，n-1）的2n步数，在主对角线上方不相交。
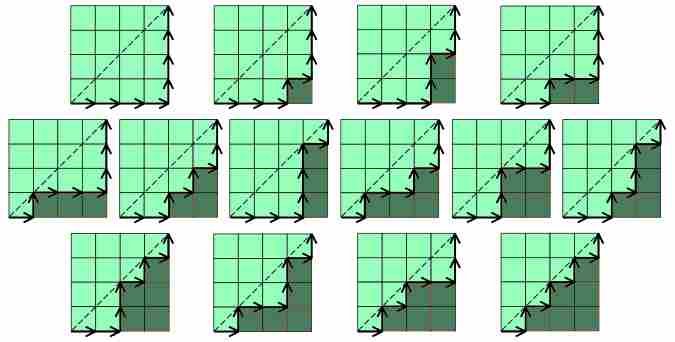
在n+1个字母的单词中插入n对括号的方法的数量，例如，对于n=2，有两种方法：（（ab）c）或（a（bc））。对于n=3，有5种方法，（（ab）（cd）），（（ab）c）d），（（a（bc））d），（a（（bc）d）），（a（b（cd））。
集合{1，…，2n}的非交叉分区数，其中每个块的大小为2。分区是非交叉的当且仅当在其平面图中，块是不相交的（即不交叉）。例如，下面两个是{1,2,3,4,5,6,7,8,9}的交叉和非交叉分区。分区{1,5,7}，{2,3,8}，{4,6}，{9}是交叉的，分区{1,5,7}，{2,3}，{4}，{6}，{8,9}是非交叉的。
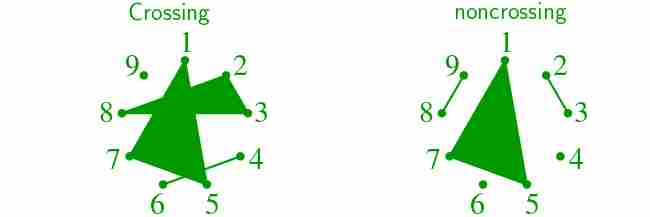
长度为2n的Dyck字数。Dyck字是由nx和ny组成的字符串，因此该字符串的初始段的Y数不超过X。例如，以下是长度为6的Dyck字： XXXYYY XYXXYY XYXYXY XXYYXY XXYXY。
用n个矩形平铺高度为n的阶梯形状的方法的数量。下图说明了n=4的情况：
连接圆上不相交和弦上的点的方法的数量。这与上面第3点类似。
形成一个“山脉”的方法有很多，有n个向上和n个向下的冲程，它们都保持在原始线之上。山脉的解释是，山脉永远不会低于地平线。
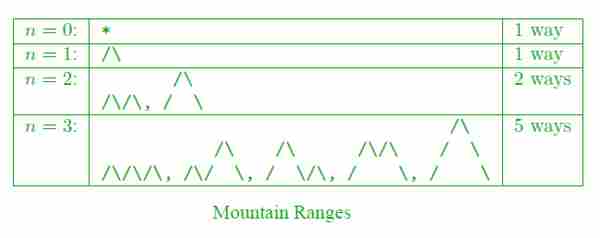
{1，…，n}的堆栈可排序排列数。如果S（w）=（1，…，n），则称置换w为堆栈可排序，其中S（w）递归定义如下：write w=unv，其中n是w中的最大元素，u和v是较短的序列，并设置S（w）=S（u）S（v）n，其中S是一个元素序列的恒等式。
避免模式123（或长度为3的任何其他模式）的{1，…，n}排列数；也就是说，没有三项递增子序列的排列数。对于n=3，这些排列是132、213、231、312和321。对于n=4，它们是1432、2143、2413、2431、3142、3214、3241、3412、3421、4132、4213、4231、4312和4321