排列是指将给定集合的所有成员排列成一个序列的过程。n个元素集合上的置换数由n,哪里“!”表示阶乘。
null
这个 置换系数 由P(n,k)表示,用于表示从一组n个元素中获得具有k个元素的有序子集的方法的数量。 从数学上来说,它是:
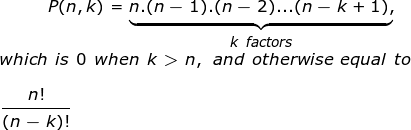
图片来源: 维基 例如:
P(10, 2) = 90P(10, 3) = 720P(10, 0) = 1P(10, 1) = 10
也可以使用以下递归公式递归计算系数:
P(n, k) = P(n-1, k) + k* P(n-1, k-1)
如果我们仔细观察,我们可以分析问题有重叠子结构,因此我们可以在这里应用动态规划。下面是一个实现相同想法的程序。
C
// A Dynamic Programming based // solution that uses table P[][] // to calculate the Permutation // Coefficient #include<bits/stdc++.h> // Returns value of Permutation // Coefficient P(n, k) int permutationCoeff( int n, int k) { int P[n + 1][k + 1]; // Calculate value of Permutation // Coefficient in bottom up manner for ( int i = 0; i <= n; i++) { for ( int j = 0; j <= std::min(i, k); j++) { // Base Cases if (j == 0) P[i][j] = 1; // Calculate value using // previously stored values else P[i][j] = P[i - 1][j] + (j * P[i - 1][j - 1]); // This step is important // as P(i,j)=0 for j>i P[i][j + 1] = 0; } } return P[n][k]; } // Driver Code int main() { int n = 10, k = 2; printf ( "Value of P(%d, %d) is %d " , n, k, permutationCoeff(n, k)); return 0; } |
JAVA
// Java code for Dynamic Programming based // solution that uses table P[][] to // calculate the Permutation Coefficient import java.io.*; import java.math.*; class GFG { // Returns value of Permutation // Coefficient P(n, k) static int permutationCoeff( int n, int k) { int P[][] = new int [n + 2 ][k + 2 ]; // Calculate value of Permutation // Coefficient in bottom up manner for ( int i = 0 ; i <= n; i++) { for ( int j = 0 ; j <= Math.min(i, k); j++) { // Base Cases if (j == 0 ) P[i][j] = 1 ; // Calculate value using previously // stored values else P[i][j] = P[i - 1 ][j] + (j * P[i - 1 ][j - 1 ]); // This step is important // as P(i,j)=0 for j>i P[i][j + 1 ] = 0 ; } } return P[n][k]; } // Driver Code public static void main(String args[]) { int n = 10 , k = 2 ; System.out.println( "Value of P( " + n + "," + k + ")" + " is " + permutationCoeff(n, k) ); } } // This code is contributed by Nikita Tiwari. |
Python3
# A Dynamic Programming based # solution that uses # table P[][] to calculate the # Permutation Coefficient # Returns value of Permutation # Coefficient P(n, k) def permutationCoeff(n, k): P = [[ 0 for i in range (k + 1 )] for j in range (n + 1 )] # Calculate value of Permutation # Coefficient in # bottom up manner for i in range (n + 1 ): for j in range ( min (i, k) + 1 ): # Base cases if (j = = 0 ): P[i][j] = 1 # Calculate value using # previously stored values else : P[i][j] = P[i - 1 ][j] + ( j * P[i - 1 ][j - 1 ]) # This step is important # as P(i, j) = 0 for j>i if (j < k): P[i][j + 1 ] = 0 return P[n][k] # Driver Code n = 10 k = 2 print ( "Value of P(" , n, ", " , k, ") is " , permutationCoeff(n, k), sep = "") # This code is contributed by Soumen Ghosh. |
C#
// C# code for Dynamic Programming based // solution that uses table P[][] to // calculate the Permutation Coefficient using System; class GFG { // Returns value of Permutation // Coefficient P(n, k) static int permutationCoeff( int n, int k) { int [,]P = new int [n + 2,k + 2]; // Calculate value of Permutation // Coefficient in bottom up manner for ( int i = 0; i <= n; i++) { for ( int j = 0; j <= Math.Min(i, k); j++) { // Base Cases if (j == 0) P[i,j] = 1; // Calculate value using previously // stored values else P[i,j] = P[i - 1,j] + (j * P[i - 1,j - 1]); // This step is important // as P(i,j)=0 for j>i P[i,j + 1] = 0; } } return P[n,k]; } // Driver Code public static void Main() { int n = 10, k = 2; Console.WriteLine( "Value of P( " + n + "," + k + ")" + " is " + permutationCoeff(n, k) ); } } // This code is contributed by anuj_67.. |
PHP
<?php // A Dynamic Programming based // solution that uses table P[][] // to calculate the Permutation // Coefficient // Returns value of Permutation // Coefficient P(n, k) function permutationCoeff( $n , $k ) { $P = array ( array ()); // Calculate value of Permutation // Coefficient in bottom up manner for ( $i = 0; $i <= $n ; $i ++) { for ( $j = 0; $j <= min( $i , $k ); $j ++) { // Base Cases if ( $j == 0) $P [ $i ][ $j ] = 1; // Calculate value using // previously stored values else $P [ $i ][ $j ] = $P [ $i - 1][ $j ] + ( $j * $P [ $i - 1][ $j - 1]); // This step is important // as P(i,j)=0 for j>i $P [ $i ][ $j + 1] = 0; } } return $P [ $n ][ $k ]; } // Driver Code $n = 10; $k = 2; echo "Value of P(" , $n , " ," , $k , ") is " , permutationCoeff( $n , $k ); // This code is contributed by anuj_67. ?> |
Javascript
<script> // Javascript code for Dynamic Programming based // solution that uses table P[][] to // calculate the Permutation Coefficient // Returns value of Permutation // Coefficient P(n, k) function permutationCoeff(n, k) { let P = new Array(n + 2); for (let i = 0; i < n + 2; i++) { P[i] = new Array(k + 2); } // Calculate value of Permutation // Coefficient in bottom up manner for (let i = 0; i <= n; i++) { for (let j = 0; j <= Math.min(i, k); j++) { // Base Cases if (j == 0) P[i][j] = 1; // Calculate value using previously // stored values else P[i][j] = P[i - 1][j] + (j * P[i - 1][j - 1]); // This step is important // as P(i,j)=0 for j>i P[i][j + 1] = 0; } } return P[n][k]; } let n = 10, k = 2; document.write( "Value of P(" + n + "," + k + ")" + " is " + permutationCoeff(n, k) ); // This code is contributed by decode2207. </script> |
输出:
Value of P(10, 2) is 90
在这里,我们可以看到时间复杂度是O(n*k),空间复杂度是O(n*k),因为程序使用辅助矩阵来存储结果。
我们能按时完成吗? 假设我们维护一个一维数组来计算n的阶乘。我们可以使用计算出的阶乘值并应用公式P(n,k)=n!/(n-k)!。下面是一个说明相同概念的程序。
C++
// A O(n) solution that uses // table fact[] to calculate // the Permutation Coefficient #include<bits/stdc++.h> using namespace std; // Returns value of Permutation // Coefficient P(n, k) int permutationCoeff( int n, int k) { int fact[n + 1]; // Base case fact[0] = 1; // Calculate value // factorials up to n for ( int i = 1; i <= n; i++) fact[i] = i * fact[i - 1]; // P(n,k) = n! / (n - k)! return fact[n] / fact[n - k]; } // Driver Code int main() { int n = 10, k = 2; cout << "Value of P(" << n << ", " << k << ") is " << permutationCoeff(n, k); return 0; } // This code is contributed by shubhamsingh10 |
C
// A O(n) solution that uses // table fact[] to calculate // the Permutation Coefficient #include<bits/stdc++.h> // Returns value of Permutation // Coefficient P(n, k) int permutationCoeff( int n, int k) { int fact[n + 1]; // base case fact[0] = 1; // Calculate value // factorials up to n for ( int i = 1; i <= n; i++) fact[i] = i * fact[i - 1]; // P(n,k) = n! / (n - k)! return fact[n] / fact[n - k]; } // Driver Code int main() { int n = 10, k = 2; printf ( "Value of P(%d, %d) is %d " , n, k, permutationCoeff(n, k) ); return 0; } |
JAVA
// A O(n) solution that uses // table fact[] to calculate // the Permutation Coefficient import java .io.*; public class GFG { // Returns value of Permutation // Coefficient P(n, k) static int permutationCoeff( int n, int k) { int []fact = new int [n+ 1 ]; // base case fact[ 0 ] = 1 ; // Calculate value // factorials up to n for ( int i = 1 ; i <= n; i++) fact[i] = i * fact[i - 1 ]; // P(n,k) = n! / (n - k)! return fact[n] / fact[n - k]; } // Driver Code static public void main (String[] args) { int n = 10 , k = 2 ; System.out.println( "Value of" + " P( " + n + ", " + k + ") is " + permutationCoeff(n, k) ); } } // This code is contributed by anuj_67. |
Python3
# A O(n) solution that uses # table fact[] to calculate # the Permutation Coefficient # Returns value of Permutation # Coefficient P(n, k) def permutationCoeff(n, k): fact = [ 0 for i in range (n + 1 )] # base case fact[ 0 ] = 1 # Calculate value # factorials up to n for i in range ( 1 , n + 1 ): fact[i] = i * fact[i - 1 ] # P(n, k) = n!/(n-k)! return int (fact[n] / fact[n - k]) # Driver Code n = 10 k = 2 print ( "Value of P(" , n, ", " , k, ") is " , permutationCoeff(n, k), sep = "") # This code is contributed # by Soumen Ghosh |
C#
// A O(n) solution that uses // table fact[] to calculate // the Permutation Coefficient using System; public class GFG { // Returns value of Permutation // Coefficient P(n, k) static int permutationCoeff( int n, int k) { int []fact = new int [n+1]; // base case fact[0] = 1; // Calculate value // factorials up to n for ( int i = 1; i <= n; i++) fact[i] = i * fact[i - 1]; // P(n,k) = n! / (n - k)! return fact[n] / fact[n - k]; } // Driver Code static public void Main () { int n = 10, k = 2; Console.WriteLine( "Value of" + " P( " + n + ", " + k + ") is " + permutationCoeff(n, k) ); } } // This code is contributed by anuj_67. |
PHP
<?php // A O(n) Solution that // uses table fact[] to // calculate the Permutation // Coefficient // Returns value of Permutation // Coefficient P(n, k) function permutationCoeff( $n , $k ) { $fact = array (); // base case $fact [0] = 1; // Calculate value // factorials up to n for ( $i = 1; $i <= $n ; $i ++) $fact [ $i ] = $i * $fact [ $i - 1]; // P(n,k)= n!/(n-k)! return $fact [ $n ] / $fact [ $n - $k ]; } // Driver Code $n = 10; $k = 2; echo "Value of P(" , $n , " " , $k , ") is " , permutationCoeff( $n , $k ) ; // This code is contributed by anuj_67. ?> |
Javascript
<script> // A O(n) solution that uses // table fact[] to calculate // the Permutation Coefficient // Returns value of Permutation // Coefficient P(n, k) function permutationCoeff(n, k) { let fact = new Array(n+1); // base case fact[0] = 1; // Calculate value // factorials up to n for (let i = 1; i <= n; i++) fact[i] = i * fact[i - 1]; // P(n,k) = n! / (n - k)! return parseInt(fact[n] / fact[n - k], 10); } let n = 10, k = 2; document.write( "Value of" + " P(" + n + ", " + k + ") is " + permutationCoeff(n, k) ); </script> |
输出:
Value of P(10, 2) is 90
O(n)时间和O(1)额外空间解
C++
// A O(n) time and O(1) extra // space solution to calculate // the Permutation Coefficient #include <iostream> using namespace std; int PermutationCoeff( int n, int k) { int P = 1; // Compute n*(n-1)*(n-2)....(n-k+1) for ( int i = 0; i < k; i++) P *= (n-i) ; return P; } // Driver Code int main() { int n = 10, k = 2; cout << "Value of P(" << n << ", " << k << ") is " << PermutationCoeff(n, k); return 0; } |
JAVA
// A O(n) time and O(1) extra // space solution to calculate // the Permutation Coefficient import java.io.*; class GFG { static int PermutationCoeff( int n, int k) { int Fn = 1 , Fk = 1 ; // Compute n! and (n-k)! for ( int i = 1 ; i <= n; i++) { Fn *= i; if (i == n - k) Fk = Fn; } int coeff = Fn / Fk; return coeff; } // Driver Code public static void main(String args[]) { int n = 10 , k = 2 ; System.out.println( "Value of P( " + n + "," + k + ") is " + PermutationCoeff(n, k) ); } } // This code is contributed by Nikita Tiwari. |
C#
// A O(n) time and O(1) extra // space solution to calculate // the Permutation Coefficient using System; class GFG { static int PermutationCoeff( int n, int k) { int Fn = 1, Fk = 1; // Compute n! and (n-k)! for ( int i = 1; i <= n; i++) { Fn *= i; if (i == n - k) Fk = Fn; } int coeff = Fn / Fk; return coeff; } // Driver Code public static void Main() { int n = 10, k = 2; Console.WriteLine( "Value of P( " + n + "," + k + ") is " + PermutationCoeff(n, k) ); } } // This code is contributed by anuj_67. |
PHP
<?php // A O(n) time and O(1) extra // space PHP solution to calculate // the Permutation Coefficient function PermutationCoeff( $n , $k ) { $Fn = 1; $Fk ; // Compute n! and (n-k)! for ( $i = 1; $i <= $n ; $i ++) { $Fn *= $i ; if ( $i == $n - $k ) $Fk = $Fn ; } $coeff = $Fn / $Fk ; return $coeff ; } // Driver Code $n = 10; $k = 2; echo "Value of P(" , $n , ", " , $k , ") is " , PermutationCoeff( $n , $k ); // This code is contributed by anuj_67. ?> |
Javascript
<script> // A O(n) time and O(1) extra // space solution to calculate // the Permutation Coefficient function PermutationCoeff(n, k) { let P = 1; // Compute n*(n-1)*(n-2)....(n-k+1) for (let i = 0; i < k; i++) P *= (n - i); return P; } // Driver code let n = 10, k = 2; document.write( "Value of P(" + n + ", " + k + ") is " + PermutationCoeff(n, k)); // This code is contributed by divyesh072019 </script> |
Python3
# A O(n) solution that uses # table fact[] to calculate # the Permutation Coefficient # Returns value of Permutation # Coefficient P(n, k) def permutationCoeff(n, k): f = 1 for i in range (k): #P(n,k)=n*(n-1)*(n-2)*....(n-k-1) f * = (n - i) return f #This code is contributed by Suyash Saxena # Driver Code n = 10 k = 2 print ( "Value of P(" , n, ", " , k, ") is " , permutationCoeff(n, k)) |
输出:
Value of P(10, 2) is 90
感谢希瓦·库马尔提出这个解决方案。 本文由 阿什图什·库马尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



