给定浮点数x上的函数f(x)和两个数“a”和“b”,使得f(a)*f(b)<0且f(x)在[a,b]中是连续的。这里f(x)表示代数或超越方程。求区间[a,b]中函数的根(或求x的值,使f(x)为0)。
null
Input: A function of x, for example x3 – x2 + 2. And two values: a = -200 and b = 300 such that f(a)*f(b) < 0, i.e., f(a) and f(b) have opposite signs.Output: The value of root is : -1.00 OR any other value close to root.
我们强烈建议将下面的帖子作为这篇帖子的先决条件。 代数和超越方程的解|集1(二分法) 本文讨论了假定位的方法。这种方法也被称为Regula Falsi或和弦法。 与二分法的相似之处:
- 同样的假设:该方法还假设函数在[a,b]中是连续的,并且给定两个数“a”和“b”,使得f(a)*f(b)<0。
- 总是收敛:和二分法一样,它总是收敛,通常比二分法快得多,但有时比二分法慢得多。
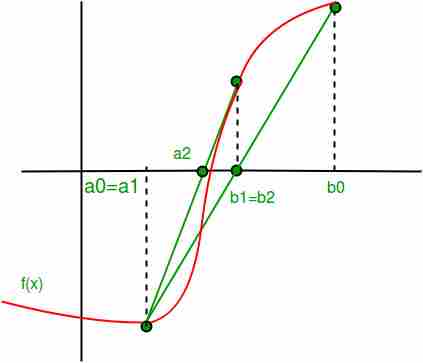
与二分法的区别: 它的不同之处在于,我们制作了一个连接两点[a,f(a)]和[b,f(b)]的和弦。我们考虑弦接触X轴的点,并将其命名为C。 步骤:
- 写出两点连线的方程式。
y – f(a) = ( (f(b)-f(a))/(b-a) )*(x-a)Now we have to find the point which touches x axis. For that we put y = 0.so x = a - (f(a)/(f(b)-f(a))) * (b-a) x = (a*f(b) - b*f(a)) / (f(b)-f(a)) This will be our c that is c = x.
- 如果 f(c)==0,那么c是解的根。
- 其他的 f(c)!=0
- 如果 值f(a)*f(c)<0那么根位于a和c之间。所以我们重复a和c
- 否则如果 f(b)*f(c)<0那么根位于b和c之间,所以我们重复b和c。
- 其他的 给定的函数不符合其中一个假设。
因为根可能是一个浮点数,在最坏的情况下可能收敛得很慢,所以我们迭代了很多次,这样答案就更接近根了。
以下是实现。
C++
// C++ program for implementation of Bisection Method for // solving equations #include<bits/stdc++.h> using namespace std; #define MAX_ITER 1000000 // An example function whose solution is determined using // Bisection Method. The function is x^3 - x^2 + 2 double func( double x) { return x*x*x - x*x + 2; } // Prints root of func(x) in interval [a, b] void regulaFalsi( double a, double b) { if (func(a) * func(b) >= 0) { cout << "You have not assumed right a and b" ; return ; } double c = a; // Initialize result for ( int i=0; i < MAX_ITER; i++) { // Find the point that touches x axis c = (a*func(b) - b*func(a))/ (func(b) - func(a)); // Check if the above found point is root if (func(c)==0) break ; // Decide the side to repeat the steps else if (func(c)*func(a) < 0) b = c; else a = c; } cout << "The value of root is : " << c; } // Driver program to test above function int main() { // Initial values assumed double a =-200, b = 300; regulaFalsi(a, b); return 0; } |
JAVA
// java program for implementation // of Bisection Method for // solving equations import java.io.*; class GFG { static int MAX_ITER = 1000000 ; // An example function whose // solution is determined using // Bisection Method. The function // is x^3 - x^2 + 2 static double func( double x) { return (x * x * x - x * x + 2 ); } // Prints root of func(x) // in interval [a, b] static void regulaFalsi( double a, double b) { if (func(a) * func(b) >= 0 ) { System.out.println( "You have not assumed right a and b" ); } // Initialize result double c = a; for ( int i = 0 ; i < MAX_ITER; i++) { // Find the point that touches x axis c = (a * func(b) - b * func(a)) / (func(b) - func(a)); // Check if the above found point is root if (func(c) == 0 ) break ; // Decide the side to repeat the steps else if (func(c) * func(a) < 0 ) b = c; else a = c; } System.out.println( "The value of root is : " + ( int )c); } // Driver program public static void main(String[] args) { // Initial values assumed double a = - 200 , b = 300 ; regulaFalsi(a, b); } } // This article is contributed by vt_m |
Python3
# Python3 implementation of Bisection # Method for solving equations MAX_ITER = 1000000 # An example function whose solution # is determined using Bisection Method. # The function is x^3 - x^2 + 2 def func( x ): return (x * x * x - x * x + 2 ) # Prints root of func(x) in interval [a, b] def regulaFalsi( a , b): if func(a) * func(b) > = 0 : print ( "You have not assumed right a and b" ) return - 1 c = a # Initialize result for i in range (MAX_ITER): # Find the point that touches x axis c = (a * func(b) - b * func(a)) / (func(b) - func(a)) # Check if the above found point is root if func(c) = = 0 : break # Decide the side to repeat the steps elif func(c) * func(a) < 0 : b = c else : a = c print ( "The value of root is : " , '%.4f' % c) # Driver code to test above function # Initial values assumed a = - 200 b = 300 regulaFalsi(a, b) # This code is contributed by "Sharad_Bhardwaj". |
C#
// C# program for implementation // of Bisection Method for // solving equations using System; class GFG { static int MAX_ITER = 1000000; // An example function whose // solution is determined using // Bisection Method. The function // is x^3 - x^2 + 2 static double func( double x) { return (x * x * x - x * x + 2); } // Prints root of func(x) // in interval [a, b] static void regulaFalsi( double a, double b) { if (func(a) * func(b) >= 0) { Console.WriteLine( "You have not assumed right a and b" ); } // Initialize result double c = a; for ( int i = 0; i < MAX_ITER; i++) { // Find the point that touches x axis c = (a * func(b) - b * func(a)) / (func(b) - func(a)); // Check if the above found point is root if (func(c) == 0) break ; // Decide the side to repeat the steps else if (func(c) * func(a) < 0) b = c; else a = c; } Console.WriteLine( "The value of root is : " + ( int )c); } // Driver program public static void Main(String []args) { // Initial values assumed double a = -200, b = 300; regulaFalsi(a, b); } } // This code is contributed by Sam007. |
Javascript
<script> // JavaScript program for implementation of Bisection Method for // solving equations let MAX_ITER = 1000000 // An example function whose solution is determined using // Bisection Method. The function is x^3 - x^2 + 2 function func(x){ return x*x*x - x*x + 2; } // Prints root of func(x) in interval [a, b] function regulaFalsi( a, b){ if (func(a) * func(b) >= 0){ document.write( "You have not assumed right a and b" ); return ; } // Initialize result let c = a; for (let i=0; i < MAX_ITER; i++) { // Find the point that touches x axis c = Math.floor((a*func(b) - b*func(a))/ (func(b) - func(a))); // Check if the above found point is root if (func(c)==0){ break ; } // Decide the side to repeat the steps else if (func(c)*func(a) < 0){ b = c; } else { a = c; } } document.write( "The value of root is : " + c); } // Driver program to test above function // Initial values assumed let a =-200; let b = 300; regulaFalsi(a, b); </script> |
输出:
The value of root is : -1
这种方法总是收敛的,通常比二分法快得多。但最坏的情况可能非常缓慢。 我们将很快讨论解决代数和超越方程的其他方法。 参考资料: S.S.Sastry的数值分析介绍方法 https://en.wikipedia.org/wiki/False_position_method 本文由 阿比拉伊·斯密特 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



