给定浮点数x上的函数f(x)和两个数“a”和“b”,使得f(a)*f(b)<0且f(x)在[a,b]中是连续的。这里f(x)表示代数或超越方程。求区间[a,b]中函数的根(或求x的值,使f(x)为0)。 例子:
Input: A function of x, for example x3 - x2 + 2. And two values: a = -200 and b = 300 such that f(a)*f(b) < 0, i.e., f(a) and f(b) have opposite signs.Output: The value of root is : -1.0025 OR any other value with allowed deviation from root.
什么是代数函数和超越函数? 代数函数是可以用多项式形式表示的函数,如f(x)=a 1. 十、 3. +a 2. 十、 2. + ….. + e aa在哪里 1. A. 2. ,…是常数,x是变量。 超越函数是非代数函数,例如f(x)=sin(x)*x–3或f(x)=e 十、 +x 2. 或f(x)=ln(x)+x…。 什么是二分法? 该方法也称为区间减半法、二进制搜索法或二分法。该方法用于在给定区间内求方程的根,该区间的值为’x’,f(x)=0。 该方法基于 中值定理 如果f(x)是一个连续函数,并且有两个实数a和b,使得f(a)*f(b)0和f(b)<0,那么保证它们之间至少有一个根。 假设:
- f(x)是区间[a,b]中的连续函数
- f(a)*f(b)<0
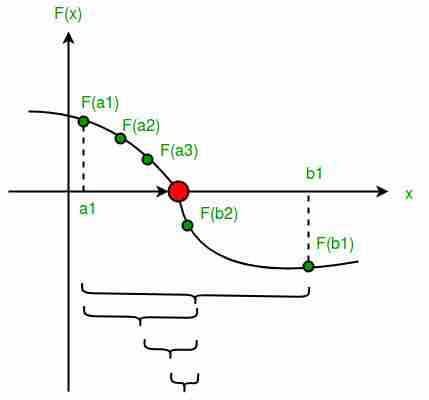
步骤:
- 找到中间点 C =(a+b)/2。
- 如果 f(c)==0,那么c是解的根。
- 其他的 f(c)!=0
- 如果 值f(a)*f(c)<0那么根位于a和c之间。所以我们重复a和c
- 否则如果 f(b)*f(c)<0那么根位于b和c之间,所以我们重复b和c。
- 其他的 给定的函数不符合其中一个假设。
因为根可能是一个浮点数,所以当a和b之间的差值小于a值时,我们重复上述步骤?(非常小的值)。
以下是上述步骤的实施。
C++
// C++ program for implementation of Bisection Method for // solving equations #include<bits/stdc++.h> using namespace std; #define EPSILON 0.01 // An example function whose solution is determined using // Bisection Method. The function is x^3 - x^2 + 2 double func( double x) { return x*x*x - x*x + 2; } // Prints root of func(x) with error of EPSILON void bisection( double a, double b) { if (func(a) * func(b) >= 0) { cout << "You have not assumed right a and b" ; return ; } double c = a; while ((b-a) >= EPSILON) { // Find middle point c = (a+b)/2; // Check if middle point is root if (func(c) == 0.0) break ; // Decide the side to repeat the steps else if (func(c)*func(a) < 0) b = c; else a = c; } cout << "The value of root is : " << c; } // Driver program to test above function int main() { // Initial values assumed double a =-200, b = 300; bisection(a, b); return 0; } |
JAVA
// Java program for implementation of Bisection Method // for solving equations class GFG{ static final float EPSILON = ( float ) 0.01 ; // An example function whose solution is determined using // Bisection Method. The function is x^3 - x^2 + 2 static double func( double x) { return x*x*x - x*x + 2 ; } // Prints root of func(x) with error of EPSILON static void bisection( double a, double b) { if (func(a) * func(b) >= 0 ) { System.out.println( "You have not assumed" + " right a and b" ); return ; } double c = a; while ((b-a) >= EPSILON) { // Find middle point c = (a+b)/ 2 ; // Check if middle point is root if (func(c) == 0.0 ) break ; // Decide the side to repeat the steps else if (func(c)*func(a) < 0 ) b = c; else a = c; } //prints value of c upto 4 decimal places System.out.printf( "The value of root is : %.4f" ,c); } // Driver program to test above function public static void main(String[] args) { // Initial values assumed double a =- 200 , b = 300 ; bisection(a, b); } // This code is contributed by Nirmal Patel } |
Python3
# Python program for implementation # of Bisection Method for # solving equations # An example function whose # solution is determined using # Bisection Method. # The function is x^3 - x^2 + 2 def func(x): return x * x * x - x * x + 2 # Prints root of func(x) # with error of EPSILON def bisection(a,b): if (func(a) * func(b) > = 0 ): print ( "You have not assumed right a and b" ) return c = a while ((b - a) > = 0.01 ): # Find middle point c = (a + b) / 2 # Check if middle point is root if (func(c) = = 0.0 ): break # Decide the side to repeat the steps if (func(c) * func(a) < 0 ): b = c else : a = c print ( "The value of root is : " , "%.4f" % c) # Driver code # Initial values assumed a = - 200 b = 300 bisection(a, b) # This code is contributed # by Anant Agarwal. |
C#
// C# program for implementation // of Bisection Method for // solving equations using System; class GFG { static float EPSILON = ( float )0.01; // An example function whose // solution is determined using // Bisection Method. The function // is x^3 - x^2 + 2 static double func( double x) { return x * x * x - x * x + 2; } // Prints root of func(x) // with error of EPSILON static void bisection( double a, double b) { if (func(a) * func(b) >= 0) { Console.WriteLine( "You have not assumed" + " right a and b" ); return ; } double c = a; while ((b - a) >= EPSILON) { // Find middle point c = (a + b) / 2; // Check if middle // point is root if (func(c) == 0.0) break ; // Decide the side // to repeat the steps else if (func(c) * func(a) < 0) b = c; else a = c; } // prints value of c // upto 4 decimal places Console.WriteLine( "The value of " + "root is : " + c); } // Driver Code static public void Main () { // Initial values assumed double a = -200, b = 300; bisection(a, b); } } // This code is contributed by ajit |
PHP
<?php // PHP program for implementation // of Bisection Method for solving // equations $EPSILON = 0.01; // An example function whose // solution is determined // using Bisection Method. // The function is x^3 - x^2 + 2 function func( $x ) { return $x * $x * $x - $x * $x + 2; } // Prints root of func(x) // with error of EPSILON function bisection( $a , $b ) { global $EPSILON ; if (func( $a ) * func( $b ) >= 0) { echo "You have not assumed " . "right a and b" , "" ; return ; } $c = $a ; while (( $b - $a ) >= $EPSILON ) { // Find middle point $c = ( $a + $b ) / 2; // Check if middle // point is root if (func( $c ) == 0.0) break ; // Decide the side to // repeat the steps else if (func( $c ) * func( $a ) < 0) $b = $c ; else $a = $c ; } echo "The value of root is : " , $c ; } // Driver Code // Initial values assumed $a =-200; $b = 300; bisection( $a , $b ); // This code is contributed by ajit ?> |
Javascript
<script> // JavaScript program for implementation // of Bisection Method for // solving equations let EPSILON = 0.01; // An example function whose solution is determined using // Bisection Method. The function is x^3 - x^2 + 2 function func(x) { return x*x*x - x*x + 2; } // Prints root of func(x) with error of EPSILON function bisection(a, b) { if (func(a) * func(b) >= 0) { document.write( "You have not assumed" + " right a and b" ); return ; } let c = a; while ((b-a) >= EPSILON) { // Find middle point c = (a+b)/2; // Check if middle point is root if (func(c) == 0.0) break ; // Decide the side to repeat the steps else if (func(c)*func(a) < 0) b = c; else a = c; } //prints value of c upto 4 decimal places document.write( "The value of " + "root is : " + c.toFixed(4)); } // Driver program // Initial values assumed let a =-200, b = 300; bisection(a, b); // This code is contributed by susmitakundugoaldanga. </script> |
输出:
The value of root is : -1.0025
时间复杂性:- 该方法的时间复杂度取决于假设值和函数。 利与弊是什么? 二分法的优点是保证了它的收敛性。对分法的缺点是不能检测多个根。 通常,对分法用于获得解的初始粗略近似值。然后使用更快的收敛方法来求解。 我们将很快讨论解决代数和超越方程的其他方法 参考资料: S.S.Sastry的数值分析介绍方法 https://en.wikipedia.org/wiki/Bisection_method 本文由 阿比拉伊·斯密特 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



