给定三个数n,r和p,计算 N C R 国防部。 例子:
Input: n = 10, r = 2, p = 13Output: 6Explanation: 10C2 is 45 and 45 % 13 is 6.
我们强烈建议您在继续解决方案之前单击此处并进行练习。
方法1:(使用动态规划)
A. 简单解决方案 首先要计算 N C R ,然后计算 N C R %p.当 N C R 它很小。 如果 N C R 它很大吗? 价值 N C R %当 N C R 无法装入变量,并导致溢出。那么计算呢 N C R 然后使用模运算符不是一个好主意,因为即使n和r的值稍大,也会出现溢出。例如,所讨论的方法 在这里 和 在这里 导致n=50和r=40溢出。 这个想法是计算 N C R 使用以下公式
C(n, r) = C(n-1, r-1) + C(n-1, r) C(n, 0) = C(n, n) = 1
上述公式和帕斯卡三角形的处理: 让我们看看上面的公式对C(4,3)是如何起作用的 1====>>n=0,C(0,0)=1 1-1=n=1,C(1,0)=1,C(1,1)=1 1-2-1=n=2,C(2,0)=1,C(2,1)=2,C(2,2)=1 1-3-3-1==>>n=3,C(3,0)=1,C(3,1)=3,C(3,2)=3,C(3,3)=1 1-4-6-4-1=>>n=4,C(4,0)=1,C(4,1)=4,C(4,2)=6,C(4,3)=4,C(4,4)=1 在这里,i上的每个循环,用第(i-1)行,建立帕斯卡三角形的第i行 上述模运算公式的扩展: 我们可以利用模算子的分布性质,用上面的公式求nCr%p。
C(n, r)%p = [ C(n-1, r-1)%p + C(n-1, r)%p ] % p C(n, 0) = C(n, n) = 1
上述公式可以通过使用2D数组的动态规划来实现。 通过一次构造一行,可以进一步优化基于二维阵列的动态规划解决方案。请参阅下面帖子中的空间优化版本以了解详细信息。 二项系数的动态规划 下面是基于上文讨论的空间优化版本的实现。
C++
// A Dynamic Programming based solution to compute nCr % p #include <bits/stdc++.h> using namespace std; // Returns nCr % p int nCrModp( int n, int r, int p) { // Optimization for the cases when r is large if (r > n - r) r = n - r; // The array C is going to store last row of // pascal triangle at the end. And last entry // of last row is nCr int C[r + 1]; memset (C, 0, sizeof (C)); C[0] = 1; // Top row of Pascal Triangle // One by constructs remaining rows of Pascal // Triangle from top to bottom for ( int i = 1; i <= n; i++) { // Fill entries of current row using previous // row values for ( int j = min(i, r); j > 0; j--) // nCj = (n-1)Cj + (n-1)C(j-1); C[j] = (C[j] + C[j - 1]) % p; } return C[r]; } // Driver program int main() { int n = 10, r = 2, p = 13; cout << "Value of nCr % p is " << nCrModp(n, r, p); return 0; } |
JAVA
// A Dynamic Programming based // solution to compute nCr % p import java.io.*; import java.util.*; import java.math.*; class GFG { // Returns nCr % p static int nCrModp( int n, int r, int p) { if (r > n - r) r = n - r; // The array C is going to store last // row of pascal triangle at the end. // And last entry of last row is nCr int C[] = new int [r + 1 ]; C[ 0 ] = 1 ; // Top row of Pascal Triangle // One by constructs remaining rows of Pascal // Triangle from top to bottom for ( int i = 1 ; i <= n; i++) { // Fill entries of current row using previous // row values for ( int j = Math.min(i, r); j > 0 ; j--) // nCj = (n-1)Cj + (n-1)C(j-1); C[j] = (C[j] + C[j - 1 ]) % p; } return C[r]; } // Driver program public static void main(String args[]) { int n = 10 , r = 2 , p = 13 ; System.out.println( "Value of nCr % p is " + nCrModp(n, r, p)); } } // This code is contributed by Nikita Tiwari. |
Python3
# A Dynamic Programming based solution to compute nCr % p # Returns nCr % p def nCrModp(n, r, p): # Optimization for the cases when r is large # compared to n-r if (r > n - r): r = n - r # The array C is going to store last row of # pascal triangle at the end. And last entry # of last row is nCr. C = [ 0 for i in range (r + 1 )] C[ 0 ] = 1 # Top row of Pascal Triangle # One by constructs remaining rows of Pascal # Triangle from top to bottom for i in range ( 1 , n + 1 ): # Fill entries of current row # using previous row values for j in range ( min (i, r), 0 , - 1 ): # nCj = (n - 1)Cj + (n - 1)C(j - 1) C[j] = (C[j] + C[j - 1 ]) % p return C[r] # Driver Program n = 10 r = 2 p = 13 print ( 'Value of nCr % p is' , nCrModp(n, r, p)) # This code is contributed by Soumen Ghosh |
C#
// A Dynamic Programming based // solution to compute nCr % p using System; class GFG { // Returns nCr % p static int nCrModp( int n, int r, int p) { // Optimization for the cases when r is large if (r > n - r) r = n - r; // The array C is going to store last // row of pascal triangle at the end. // And last entry of last row is nCr int [] C = new int [r + 1]; for ( int i = 0; i < r + 1; i++) C[i] = 0; C[0] = 1; // Top row of Pascal Triangle // One by constructs remaining rows // of Pascal Triangle from top to bottom for ( int i = 1; i <= n; i++) { // Fill entries of current row using // previous row values for ( int j = Math.Min(i, r); j > 0; j--) // nCj = (n-1)Cj + (n-1)C(j-1); C[j] = (C[j] + C[j - 1]) % p; } return C[r]; } // Driver program public static void Main() { int n = 10, r = 2, p = 13; Console.Write( "Value of nCr % p is " + nCrModp(n, r, p)); } } // This code is contributed by nitin mittal. |
PHP
<?php // A Dynamic Programming based // solution to compute nCr % p // Returns nCr % p function nCrModp( $n , $r , $p ) { // Optimization for the cases when r is large if ( $r > $n - $r ) $r = $n - $r ; // The array C is going // to store last row of // pascal triangle at // the end. And last entry // of last row is nCr $C = array (); for ( $i = 0; $i < $r + 1; $i ++) $C [ $i ] = 0; // Top row of Pascal // Triangle $C [0] = 1; // One by constructs remaining // rows of Pascal Triangle from // top to bottom for ( $i = 1; $i <= $n ; $i ++) { // Fill entries of current // row using previous row values for ( $j = Min( $i , $r ); $j > 0; $j --) // nCj = (n-1)Cj + (n-1)C(j-1); $C [ $j ] = ( $C [ $j ] + $C [ $j - 1]) % $p ; } return $C [ $r ]; } // Driver Code $n = 10; $r = 2; $p = 13; echo "Value of nCr % p is " , nCrModp( $n , $r , $p ); // This code is contributed // by anuj_67. ?> |
Javascript
<script> // A Dynamic Programming based // solution to compute nCr % p // Returns nCr % p function nCrModp(n,r,p) { if (r > n - r) r = n - r; // The array C is going to store last // row of pascal triangle at the end. // And last entry of last row is nCr let C = new Array(r + 1); for (let i = 0; i < r + 1; i++) C[i] = 0; C[0] = 1; // Top row of Pascal Triangle // One by constructs remaining rows of Pascal // Triangle from top to bottom for (let i = 1; i <= n; i++) { // Fill entries of current row using previous // row values for (let j = Math.min(i, r); j > 0; j--) // nCj = (n-1)Cj + (n-1)C(j-1); C[j] = (C[j] + C[j - 1]) % p; } return C[r]; } // Driver program let n = 10, r = 2, p = 13; document.write( "Value of nCr % p is " + nCrModp(n, r, p)); // This code is contributed by avanitrachhadiya2155 </script> |
Value of nCr % p is 6
上述解的时间复杂度为O(n*r),需要O(r)空间。以上问题有更多更好的解决方案。 计算nCr%p |集2(卢卡斯定理) 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
方法2(使用Pascal三角形和Dynamic Pro)
另一种方法是利用帕斯卡三角形的概念。而不是计算 N C R 从n=0到n=n的每n的值,该方法旨在使用第n行本身进行计算。该方法通过找出 N C R 和 N C r-1 .
FORMULA: C(n,r)=C(n,r-1)* (n-r+1)/rExample:For instance, take n=5 and r=3.Input: n = 5, r = 3, p = 1000000007Output: 6Explanation: 5C3 is 10 and 10 % 100000007 is 10.As per the formula,C(5,3)=5!/(3!)*(2!)C(5,3)=10Also,C(5,2)=5!/(2!)*(3!)C(5,2)=10Let's try applying the above formula.C(n,r)=C(n,r-1)* (n-r+1)/rC(5,3)=C(5,2)*(5-3+1)/3C(5,3)=C(5,2)*1C(5,3)=10*1
上面的例子表明,通过计算C(n,r-1)并将结果与(n-r+1)/r项相乘,可以很容易地计算出C(n,r)。但是这种乘法可能会导致n的大值出现整数溢出。为了解决这种情况,使用模乘和模除概念,以实现整数溢出方面的优化。
让我们来看看如何为同样的问题构建Pascal三角形。
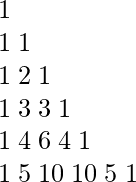
1D数组声明可以进一步优化,只需声明一个变量即可执行计算。然而,整数溢出也需要其他函数才能最终实现。
下面的帖子提到了 时空优化 二元系数计算的实现。
C++
// C++ program to find the nCr%p // based on optimal Dynamic // Programming implementation and // Pascal Triangle concepts #include <bits/stdc++.h> using namespace std; // Returns (a * b) % mod long long moduloMultiplication( long long a, long long b, long long mod) { // Initialize result long long res = 0; // Update a if it is more than // or equal to mod a %= mod; while (b) { // If b is odd, add a with result if (b & 1) res = (res + a) % mod; // Here we assume that doing 2*a // doesn't cause overflow a = (2 * a) % mod; b >>= 1; // b = b / 2 } return res; } // C++ function for extended Euclidean Algorithm long long int gcdExtended( long long int a, long long int b, long long int * x, long long int * y); // Function to find modulo inverse of b. It returns // -1 when inverse doesn't exists long long int modInverse( long long int b, long long int m) { long long int x, y; // used in extended GCD algorithm long long int g = gcdExtended(b, m, &x, &y); // Return -1 if b and m are not co-prime if (g != 1) return -1; // m is added to handle negative x return (x % m + m) % m; } // C function for extended Euclidean Algorithm (used to // find modular inverse. long long int gcdExtended( long long int a, long long int b, long long int * x, long long int * y) { // Base Case if (a == 0) { *x = 0, *y = 1; return b; } // To store results of recursive call long long int x1, y1; long long int gcd = gcdExtended(b % a, a, &x1, &y1); // Update x and y using results of recursive // call *x = y1 - (b / a) * x1; *y = x1; return gcd; } // Function to compute a/b under modlo m long long int modDivide( long long int a, long long int b, long long int m) { a = a % m; long long int inv = modInverse(b, m); if (inv == -1) // cout << "Division not defined"; return 0; else return (inv * a) % m; } // Function to calculate nCr % p int nCr( int n, int r, int p) { // Edge Case which is not possible if (r > n) return 0; // Optimization for the cases when r is large if (r > n - r) r = n - r; // x stores the current result at long long int x = 1; // each iteration // Initialized to 1 as nC0 is always 1. for ( int i = 1; i <= r; i++) { // Formula derived for calculating result is // C(n,r-1)*(n-r+1)/r // Function calculates x*(n-i+1) % p. x = moduloMultiplication(x, (n + 1 - i), p); // Function calculates x/i % p. x = modDivide(x, i, p); } return x; } // Driver Code int main() { long long int n = 5, r = 3, p = 1000000007; cout << "Value of nCr % p is " << nCr(n, r, p); return 0; } |
Value of nCr % p is 10
复杂性分析:
- 上述代码需要额外的O(1)空间进行计算。
- 计算nCr%p所需的时间为O(n)级。
本文的改进是 雅利安·古普塔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



