给定一组n个元素,找出划分它的多种方法。 例如:
Input: n = 2Output: Number of ways = 2Explanation: Let the set be {1, 2} { {1}, {2} } { {1, 2} }Input: n = 3Output: Number of ways = 5Explanation: Let the set be {1, 2, 3} { {1}, {2}, {3} } { {1}, {2, 3} } { {2}, {1, 3} } { {3}, {1, 2} } { {1, 2, 3} }.
以上问题的解决方案是 铃号 . 铃号是多少? 允许 S(n,k) n个元素划分成k个集合的总数。当k=1到n时,第n个钟形数的值是S(n,k)的和。 ![]() S(n,k)的值可以递归地定义为,S(n+1,k)=k*S(n,k)+S(n,k-1) 上述递归公式是如何工作的? 当我们向k个分区添加第(n+1)个元素时,有两种可能性。 1) 它作为单个元素集添加到现有分区,即S(n,k-1) 2) 它被添加到每个分区的所有集合中,即k*S(n,k) S(n,k)被称为 第二类斯特林数 前几个钟号是1,1,2,5,15,52,203…。 A. 简单方法 计算第n个钟形数就是逐个计算k=1到n的S(n,k),并返回所有计算值的总和。参考 这 用于S(n,k)的计算。 A. 更好的方法 就是使用 钟形三角形 下面是前几个钟形数字的钟形三角形示例。
S(n,k)的值可以递归地定义为,S(n+1,k)=k*S(n,k)+S(n,k-1) 上述递归公式是如何工作的? 当我们向k个分区添加第(n+1)个元素时,有两种可能性。 1) 它作为单个元素集添加到现有分区,即S(n,k-1) 2) 它被添加到每个分区的所有集合中,即k*S(n,k) S(n,k)被称为 第二类斯特林数 前几个钟号是1,1,2,5,15,52,203…。 A. 简单方法 计算第n个钟形数就是逐个计算k=1到n的S(n,k),并返回所有计算值的总和。参考 这 用于S(n,k)的计算。 A. 更好的方法 就是使用 钟形三角形 下面是前几个钟形数字的钟形三角形示例。
11 22 3 55 7 10 1515 20 27 37 52
这个三角形是用下面的公式构造的。
// If this is first column of current row 'i'If j == 0 // Then copy last entry of previous row // Note that i'th row has i entries Bell(i, j) = Bell(i-1, i-1) // If this is not first column of current rowElse // Then this element is sum of previous element // in current row and the element just above the // previous element Bell(i, j) = Bell(i-1, j-1) + Bell(i, j-1)
理解 然后Bell(n,k)计算集合{1,2,…,n+1}的分区数,其中元素k+1是其集合中可以单独存在的最大元素。 例如,Bell(3,2)是3,它是{1,2,3,4}的分区数,其中3是最大的单态元素。有三个这样的分区:
{1}, {2, 4}, {3} {1, 4}, {2}, {3} {1, 2, 4}, {3}.
下面是基于动态规划的上述递归公式的实现。
C++
// A C++ program to find n'th Bell number #include<iostream> using namespace std; int bellNumber( int n) { int bell[n+1][n+1]; bell[0][0] = 1; for ( int i=1; i<=n; i++) { // Explicitly fill for j = 0 bell[i][0] = bell[i-1][i-1]; // Fill for remaining values of j for ( int j=1; j<=i; j++) bell[i][j] = bell[i-1][j-1] + bell[i][j-1]; } return bell[n][0]; } // Driver program int main() { for ( int n=0; n<=5; n++) cout << "Bell Number " << n << " is " << bellNumber(n) << endl; return 0; } |
JAVA
// Java program to find n'th Bell number import java.io.*; class GFG { // Function to find n'th Bell Number static int bellNumber( int n) { int [][] bell = new int [n+ 1 ][n+ 1 ]; bell[ 0 ][ 0 ] = 1 ; for ( int i= 1 ; i<=n; i++) { // Explicitly fill for j = 0 bell[i][ 0 ] = bell[i- 1 ][i- 1 ]; // Fill for remaining values of j for ( int j= 1 ; j<=i; j++) bell[i][j] = bell[i- 1 ][j- 1 ] + bell[i][j- 1 ]; } return bell[n][ 0 ]; } // Driver program public static void main (String[] args) { for ( int n= 0 ; n<= 5 ; n++) System.out.println( "Bell Number " + n + " is " +bellNumber(n)); } } // This code is contributed by Pramod Kumar |
Python3
# A Python program to find n'th Bell number def bellNumber(n): bell = [[ 0 for i in range (n + 1 )] for j in range (n + 1 )] bell[ 0 ][ 0 ] = 1 for i in range ( 1 , n + 1 ): # Explicitly fill for j = 0 bell[i][ 0 ] = bell[i - 1 ][i - 1 ] # Fill for remaining values of j for j in range ( 1 , i + 1 ): bell[i][j] = bell[i - 1 ][j - 1 ] + bell[i][j - 1 ] return bell[n][ 0 ] # Driver program for n in range ( 6 ): print ( 'Bell Number' , n, 'is' , bellNumber(n)) # This code is contributed by Soumen Ghosh |
C#
// C# program to find n'th Bell number using System; class GFG { // Function to find n'th // Bell Number static int bellNumber( int n) { int [,] bell = new int [n + 1, n + 1]; bell[0, 0] = 1; for ( int i = 1; i <= n; i++) { // Explicitly fill for j = 0 bell[i, 0] = bell[i - 1, i - 1]; // Fill for remaining values of j for ( int j = 1; j <= i; j++) bell[i, j] = bell[i - 1, j - 1] + bell[i, j - 1]; } return bell[n, 0]; } // Driver Code public static void Main () { for ( int n = 0; n <= 5; n++) Console.WriteLine( "Bell Number " + n + " is " +bellNumber(n)); } } // This code is contributed by nitin mittal. |
PHP
<?php // A PHP program to find // n'th Bell number // function that returns // n'th bell number function bellNumber( $n ) { $bell [0][0] = 1; for ( $i = 1; $i <= $n ; $i ++) { // Explicitly fill for j = 0 $bell [ $i ][0] = $bell [ $i - 1] [ $i - 1]; // Fill for remaining // values of j for ( $j = 1; $j <= $i ; $j ++) $bell [ $i ][ $j ] = $bell [ $i - 1][ $j - 1] + $bell [ $i ][ $j - 1]; } return $bell [ $n ][0]; } // Driver Code for ( $n = 0; $n <= 5; $n ++) echo ( "Bell Number " . $n . " is " . bellNumber( $n ) . "" ); // This code is contributed by Ajit. ?> |
Javascript
<script> // Javascript program to find n'th Bell number // Function to find n'th Bell Number function bellNumber(n) { let bell = new Array(n+1); for (let i = 0; i < n + 1; i++) { bell[i] = new Array(n + 1); } bell[0][0] = 1; for (let i=1; i<=n; i++) { // Explicitly fill for j = 0 bell[i][0] = bell[i-1][i-1]; // Fill for remaining values of j for (let j=1; j<=i; j++) bell[i][j] = bell[i-1][j-1] + bell[i][j-1]; } return bell[n][0]; } for (let n=0; n<=5; n++) document.write( "Bell Number " + n + " is " +bellNumber(n) + "</br>" ); </script> |
输出:
Bell Number 0 is 1Bell Number 1 is 1Bell Number 2 is 2Bell Number 3 is 5Bell Number 4 is 15Bell Number 5 is 52
上述解的时间复杂度为O(n) 2. ).我们很快就会讨论计算贝尔数的其他更有效的方法。 另一个可以用钟形数字解决的问题 . 一个数字是 无平方 如果它不能被除1以外的完美正方形整除。例如,6是一个无平方数,但12不是,因为它可以被4整除。 给定一个无平方数x,求x的不同乘法分区的个数。乘法分区的个数是Bell(n),其中n是x的素数因子的个数。例如x=30,有3个素数因子2、3和5。所以答案是Bell(3),也就是5。5个分区分别为1 x 30、2 x 15、3 x 10、5 x 6和2 x 3 x 5。 练习: 上述实现会导致n值稍大的算术溢出。请扩展上述程序,以便在模100000007下计算结果,以避免溢出。 参考: https://en.wikipedia.org/wiki/Bell_number https://en.wikipedia.org/wiki/Bell_triangle 本文由 拉吉耶夫·阿格拉瓦尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论。
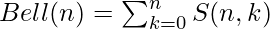


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



