深度优先遍历(或搜索) 对于一个图,它类似于 树的深度优先遍历(DFS) 这里唯一的问题是,与树不同,图可能包含循环,因此一个节点可能会被访问两次。要避免多次处理节点,请使用布尔数组。
null
例子:
输入: n=4,e=6 0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3 输出: 来自顶点1的DFS:1 2 0 3 说明: DFS图:
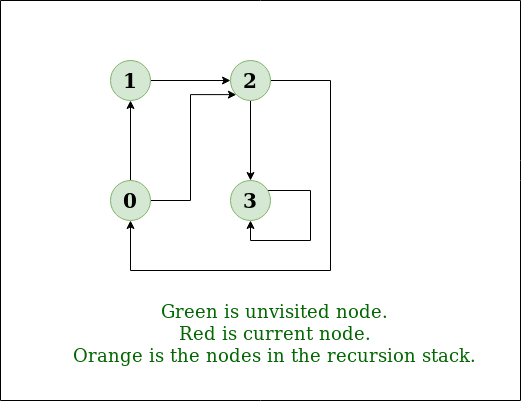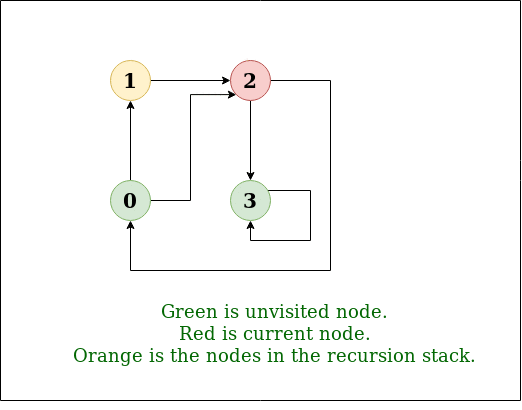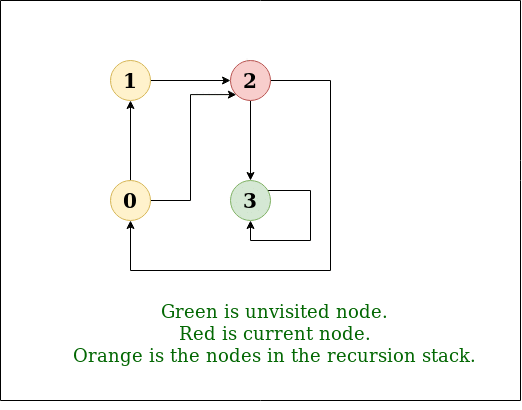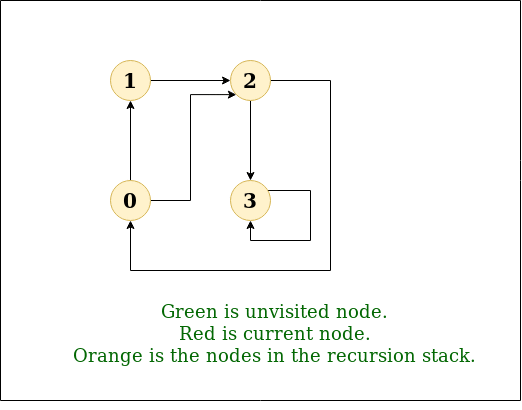
输入: n=4,e=6 2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3 输出: 来自顶点2的DFS:2 0 1 3 说明: DFS图:
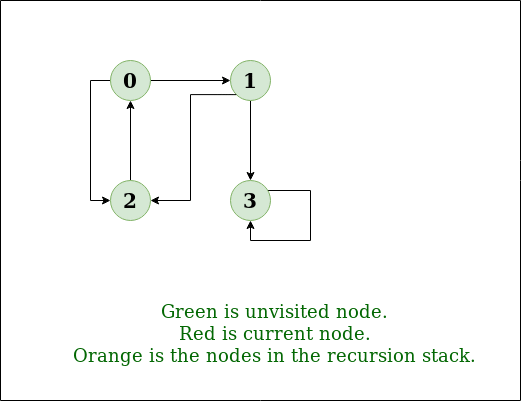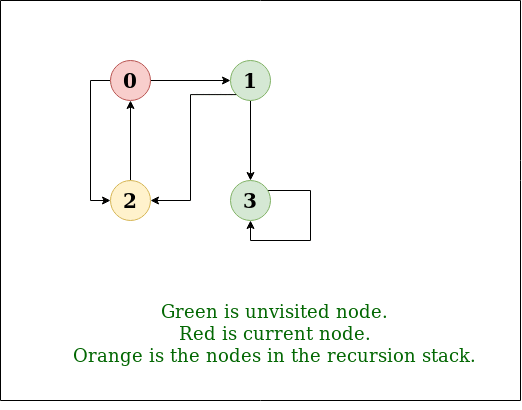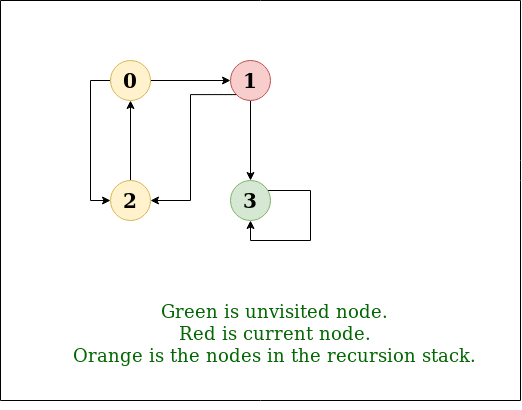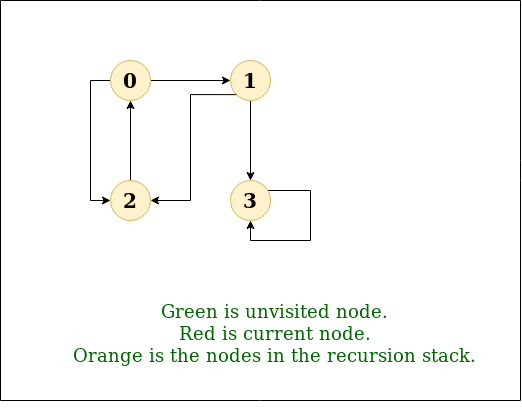
DFS的递归实现已经讨论过: 以前的职位 . 解决方案:
- 方法: 深度优先搜索是一种遍历或搜索树或图数据结构的算法。该算法从根节点开始(在图中选择任意节点作为根节点),并在回溯之前尽可能沿着每个分支进行探索。基本思想是从根或任意节点开始,标记节点,移动到相邻的未标记节点,继续循环,直到没有未标记的相邻节点。然后回溯并检查其他未标记的节点,并遍历它们。最后打印路径中的节点。 迭代DFS和递归DFS之间的唯一区别是递归堆栈被节点堆栈所取代。
- 算法:
- 创建了一组节点并访问了阵列。
- 在堆栈中插入根。
- 运行循环,直到堆栈不为空。
- 从堆栈中弹出元素并打印元素。
- 对于当前节点的每个相邻和未访问的节点,标记该节点并将其插入堆栈中。
- 迭代DFS的实现: 这与 BFS 唯一的区别是队列被堆栈取代。
C++
// An Iterative C++ program to do DFS traversal from // a given source vertex. DFS(int s) traverses vertices // reachable from s. #include<bits/stdc++.h> using namespace std; // This class represents a directed graph using adjacency // list representation class Graph { int V; // No. of vertices list< int > *adj; // adjacency lists public : Graph( int V); // Constructor void addEdge( int v, int w); // to add an edge to graph void DFS( int s); // prints all vertices in DFS manner // from a given source. }; Graph::Graph( int V) { this ->V = V; adj = new list< int >[V]; } void Graph::addEdge( int v, int w) { adj[v].push_back(w); // Add w to v’s list. } // prints all not yet visited vertices reachable from s void Graph::DFS( int s) { // Initially mark all vertices as not visited vector< bool > visited(V, false ); // Create a stack for DFS stack< int > stack; // Push the current source node. stack.push(s); while (!stack.empty()) { // Pop a vertex from stack and print it int s = stack.top(); stack.pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (!visited[s]) { cout << s << " " ; visited[s] = true ; } // Get all adjacent vertices of the popped vertex s // If a adjacent has not been visited, then push it // to the stack. for ( auto i = adj[s].begin(); i != adj[s].end(); ++i) if (!visited[*i]) stack.push(*i); } } // Driver program to test methods of graph class int main() { Graph g(5); // Total 5 vertices in graph g.addEdge(1, 0); g.addEdge(0, 2); g.addEdge(2, 1); g.addEdge(0, 3); g.addEdge(1, 4); cout << "Following is Depth First Traversal" ; g.DFS(0); return 0; } |
JAVA
//An Iterative Java program to do DFS traversal from //a given source vertex. DFS(int s) traverses vertices //reachable from s. import java.util.*; public class GFG { // This class represents a directed graph using adjacency // list representation static class Graph { int V; //Number of Vertices LinkedList<Integer>[] adj; // adjacency lists //Constructor Graph( int V) { this .V = V; adj = new LinkedList[V]; for ( int i = 0 ; i < adj.length; i++) adj[i] = new LinkedList<Integer>(); } //To add an edge to graph void addEdge( int v, int w) { adj[v].add(w); // Add w to v’s list. } // prints all not yet visited vertices reachable from s void DFS( int s) { // Initially mark all vertices as not visited Vector<Boolean> visited = new Vector<Boolean>(V); for ( int i = 0 ; i < V; i++) visited.add( false ); // Create a stack for DFS Stack<Integer> stack = new Stack<>(); // Push the current source node stack.push(s); while (stack.empty() == false ) { // Pop a vertex from stack and print it s = stack.peek(); stack.pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (visited.get(s) == false ) { System.out.print(s + " " ); visited.set(s, true ); } // Get all adjacent vertices of the popped vertex s // If a adjacent has not been visited, then push it // to the stack. Iterator<Integer> itr = adj[s].iterator(); while (itr.hasNext()) { int v = itr.next(); if (!visited.get(v)) stack.push(v); } } } } // Driver program to test methods of graph class public static void main(String[] args) { // Total 5 vertices in graph Graph g = new Graph( 5 ); g.addEdge( 1 , 0 ); g.addEdge( 0 , 2 ); g.addEdge( 2 , 1 ); g.addEdge( 0 , 3 ); g.addEdge( 1 , 4 ); System.out.println( "Following is the Depth First Traversal" ); g.DFS( 0 ); } } |
Python3
# An Iterative Python program to do DFS traversal from # a given source vertex. DFS(int s) traverses vertices # reachable from s. # This class represents a directed graph using adjacency # list representation class Graph: def __init__( self ,V): # Constructor self .V = V # No. of vertices self .adj = [[] for i in range (V)] # adjacency lists def addEdge( self ,v, w): # to add an edge to graph self .adj[v].append(w) # Add w to v’s list. # prints all not yet visited vertices reachable from s def DFS( self ,s): # prints all vertices in DFS manner from a given source. # Initially mark all vertices as not visited visited = [ False for i in range ( self .V)] # Create a stack for DFS stack = [] # Push the current source node. stack.append(s) while ( len (stack)): # Pop a vertex from stack and print it s = stack[ - 1 ] stack.pop() # Stack may contain same vertex twice. So # we need to print the popped item only # if it is not visited. if ( not visited[s]): print (s,end = ' ' ) visited[s] = True # Get all adjacent vertices of the popped vertex s # If a adjacent has not been visited, then push it # to the stack. for node in self .adj[s]: if ( not visited[node]): stack.append(node) # Driver program to test methods of graph class g = Graph( 5 ); # Total 5 vertices in graph g.addEdge( 1 , 0 ); g.addEdge( 0 , 2 ); g.addEdge( 2 , 1 ); g.addEdge( 0 , 3 ); g.addEdge( 1 , 4 ); print ( "Following is Depth First Traversal" ) g.DFS( 0 ) # This code is contributed by ankush_953 |
C#
// An Iterative C# program to do DFS traversal from // a given source vertex. DFS(int s) traverses vertices // reachable from s. using System; using System.Collections.Generic; class GFG { // This class represents a directed graph using adjacency // list representation public class Graph { public int V; // Number of Vertices public LinkedList< int >[] adj; // adjacency lists // Constructor public Graph( int V) { this .V = V; adj = new LinkedList< int >[V]; for ( int i = 0; i < adj.Length; i++) adj[i] = new LinkedList< int >(); } // To add an edge to graph public void addEdge( int v, int w) { adj[v].AddLast(w); // Add w to v’s list. } // prints all not yet visited vertices reachable from s public void DFS( int s) { // Initially mark all vertices as not visited Boolean []visited = new Boolean[V]; // Create a stack for DFS Stack< int > stack = new Stack< int >(); // Push the current source node stack.Push(s); while (stack.Count > 0) { // Pop a vertex from stack and print it s = stack.Peek(); stack.Pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (visited[s] == false ) { Console.Write(s + " " ); visited[s] = true ; } // Get all adjacent vertices of the popped vertex s // If a adjacent has not been visited, then push it // to the stack. foreach ( int v in adj[s]) { if (!visited[v]) stack.Push(v); } } } } // Driver code public static void Main(String []args) { // Total 5 vertices in graph Graph g = new Graph(5); g.addEdge(1, 0); g.addEdge(0, 2); g.addEdge(2, 1); g.addEdge(0, 3); g.addEdge(1, 4); Console.Write( "Following is the Depth First Traversal" ); g.DFS(0); } } // This code is contributed by Arnasb Kundu |
Javascript
<script> // An Iterative Javascript program to // do DFS traversal from a given source // vertex. DFS(int s) traverses vertices // reachable from s. // This class represents a directed graph // using adjacency list representation class Graph{ constructor(V) { this .V = V; this .adj = new Array(V); for (let i = 0; i < this .adj.length; i++) this .adj[i] = []; } // To add an edge to graph addEdge(v, w) { // Add w to v’s list. this .adj[v].push(w); } // Prints all not yet visited // vertices reachable from s DFS(s) { // Initially mark all vertices as not visited let visited = []; for (let i = 0; i < this .V; i++) visited.push( false ); // Create a stack for DFS let stack = []; // Push the current source node stack.push(s); while (stack.length != 0) { // Pop a vertex from stack and print it s = stack.pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (visited[s] == false ) { document.write(s + " " ); visited[s] = true ; } // Get all adjacent vertices of the // popped vertex s. If a adjacent has // not been visited, then push it // to the stack. for (let node = 0; node < this .adj[s].length; node++) { if (!visited[ this .adj[s][node]]) stack.push( this .adj[s][node]) } } } } // Driver code // Total 5 vertices in graph let g = new Graph(5); g.addEdge(1, 0); g.addEdge(0, 2); g.addEdge(2, 1); g.addEdge(0, 3); g.addEdge(1, 4); document.write( "Following is the Depth " + "First Traversal<br>" ); g.DFS(0); // This code is contributed by rag2127 </script> |
输出:
Following is Depth First Traversal0 3 2 1 4
- 复杂性分析:
- 时间复杂性: O(V+E),其中V是图中的顶点数,E是图中的边数。
- 空间复杂性: O(V)。因为需要一个V大小的额外访问阵列。
对上述解决方案的修改 : 注意,上面的实现只打印从给定顶点可以到达的顶点。例如,如果删除了边缘0-3和0-2,则上述程序将只打印0。要打印图形的所有顶点,请为每个未访问的顶点调用DFS。
实施:
C++
// An Iterative C++ program to do DFS traversal from // a given source vertex. DFS(int s) traverses vertices // reachable from s. #include<bits/stdc++.h> using namespace std; // This class represents a directed graph using adjacency // list representation class Graph { int V; // No. of vertices list< int > *adj; // adjacency lists public : Graph( int V); // Constructor void addEdge( int v, int w); // to add an edge to graph void DFS(); // prints all vertices in DFS manner // prints all not yet visited vertices reachable from s void DFSUtil( int s, vector< bool > &visited); }; Graph::Graph( int V) { this ->V = V; adj = new list< int >[V]; } void Graph::addEdge( int v, int w) { adj[v].push_back(w); // Add w to v’s list. } // prints all not yet visited vertices reachable from s void Graph::DFSUtil( int s, vector< bool > &visited) { // Create a stack for DFS stack< int > stack; // Push the current source node. stack.push(s); while (!stack.empty()) { // Pop a vertex from stack and print it int s = stack.top(); stack.pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (!visited[s]) { cout << s << " " ; visited[s] = true ; } // Get all adjacent vertices of the popped vertex s // If a adjacent has not been visited, then push it // to the stack. for ( auto i = adj[s].begin(); i != adj[s].end(); ++i) if (!visited[*i]) stack.push(*i); } } // prints all vertices in DFS manner void Graph::DFS() { // Mark all the vertices as not visited vector< bool > visited(V, false ); for ( int i = 0; i < V; i++) if (!visited[i]) DFSUtil(i, visited); } // Driver program to test methods of graph class int main() { Graph g(5); // Total 5 vertices in graph g.addEdge(1, 0); g.addEdge(2, 1); g.addEdge(3, 4); g.addEdge(4, 0); cout << "Following is Depth First Traversal" ; g.DFS(); return 0; } |
JAVA
//An Iterative Java program to do DFS traversal from //a given source vertex. DFS() traverses vertices //reachable from s. import java.util.*; public class GFG { // This class represents a directed graph using adjacency // list representation static class Graph { int V; //Number of Vertices LinkedList<Integer>[] adj; // adjacency lists //Constructor Graph( int V) { this .V = V; adj = new LinkedList[V]; for ( int i = 0 ; i < adj.length; i++) adj[i] = new LinkedList<Integer>(); } //To add an edge to graph void addEdge( int v, int w) { adj[v].add(w); // Add w to v’s list. } // prints all not yet visited vertices reachable from s void DFSUtil( int s, Vector<Boolean> visited) { // Create a stack for DFS Stack<Integer> stack = new Stack<>(); // Push the current source node stack.push(s); while (stack.empty() == false ) { // Pop a vertex from stack and print it s = stack.peek(); stack.pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (visited.get(s) == false ) { System.out.print(s + " " ); visited.set(s, true ); } // Get all adjacent vertices of the popped vertex s // If a adjacent has not been visited, then push it // to the stack. Iterator<Integer> itr = adj[s].iterator(); while (itr.hasNext()) { int v = itr.next(); if (!visited.get(v)) stack.push(v); } } } // prints all vertices in DFS manner void DFS() { Vector<Boolean> visited = new Vector<Boolean>(V); // Mark all the vertices as not visited for ( int i = 0 ; i < V; i++) visited.add( false ); for ( int i = 0 ; i < V; i++) if (!visited.get(i)) DFSUtil(i, visited); } } // Driver program to test methods of graph class public static void main(String[] args) { Graph g = new Graph( 5 ); g.addEdge( 1 , 0 ); g.addEdge( 2 , 1 ); g.addEdge( 3 , 4 ); g.addEdge( 4 , 0 ); System.out.println( "Following is Depth First Traversal" ); g.DFS(); } } |
Python3
# An Iterative Python3 program to do DFS # traversal from a given source vertex. # DFS(s) traverses vertices reachable from s. class Graph: def __init__( self , V): self .V = V self .adj = [[] for i in range (V)] def addEdge( self , v, w): self .adj[v].append(w) # Add w to v’s list. # prints all not yet visited vertices # reachable from s def DFSUtil( self , s, visited): # Create a stack for DFS stack = [] # Push the current source node. stack.append(s) while ( len (stack) ! = 0 ): # Pop a vertex from stack and print it s = stack.pop() # Stack may contain same vertex twice. # So we need to print the popped item only # if it is not visited. if ( not visited[s]): print (s, end = " " ) visited[s] = True # Get all adjacent vertices of the # popped vertex s. If a adjacent has not # been visited, then push it to the stack. i = 0 while i < len ( self .adj[s]): if ( not visited[ self .adj[s][i]]): stack.append( self .adj[s][i]) i + = 1 # prints all vertices in DFS manner def DFS( self ): # Mark all the vertices as not visited visited = [ False ] * self .V for i in range ( self .V): if ( not visited[i]): self .DFSUtil(i, visited) # Driver Code if __name__ = = '__main__' : g = Graph( 5 ) # Total 5 vertices in graph g.addEdge( 1 , 0 ) g.addEdge( 2 , 1 ) g.addEdge( 3 , 4 ) g.addEdge( 4 , 0 ) print ( "Following is Depth First Traversal" ) g.DFS() # This code is contributed by PranchalK |
C#
// An Iterative C# program to do DFS traversal from // a given source vertex. DFS() traverses vertices // reachable from s. using System; using System.Collections.Generic; class GFG { // This class represents a directed graph using adjacency // list representation class Graph { public int V; // Number of Vertices public List< int >[] adj; // adjacency lists // Constructor public Graph( int V) { this .V = V; adj = new List< int >[V]; for ( int i = 0; i < adj.Length; i++) adj[i] = new List< int >(); } // To add an edge to graph public void addEdge( int v, int w) { adj[v].Add(w); // Add w to v’s list. } // prints all not yet visited vertices reachable from s public void DFSUtil( int s, List<Boolean> visited) { // Create a stack for DFS Stack< int > stack = new Stack< int >(); // Push the current source node stack.Push(s); while (stack.Count != 0) { // Pop a vertex from stack and print it s = stack.Peek(); stack.Pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (visited[s] == false ) { Console.Write(s + " " ); visited[s] = true ; } // Get all adjacent vertices of the popped vertex s // If a adjacent has not been visited, then push it // to the stack. foreach ( int itr in adj[s]) { int v = itr; if (!visited[v]) stack.Push(v); } } } // prints all vertices in DFS manner public void DFS() { List<Boolean> visited = new List<Boolean>(V); // Mark all the vertices as not visited for ( int i = 0; i < V; i++) visited.Add( false ); for ( int i = 0; i < V; i++) if (!visited[i]) DFSUtil(i, visited); } } // Driver code public static void Main(String[] args) { Graph g = new Graph(5); g.addEdge(1, 0); g.addEdge(2, 1); g.addEdge(3, 4); g.addEdge(4, 0); Console.WriteLine( "Following is Depth First Traversal" ); g.DFS(); } } // This code is contributed by 29AjayKumar |
Javascript
<script> //An Iterative Javascript program to do DFS traversal from //a given source vertex. DFS() traverses vertices //reachable from s. // This class represents a directed graph using adjacency // list representation class Graph { //Constructor constructor(V) { this .V=V; this .adj = new Array(V); for (let i = 0; i < this .adj.length; i++) this .adj[i] = []; } //To add an edge to graph addEdge(v,w) { this .adj[v].push(w); // Add w to v’s list. } // prints all not yet visited vertices reachable from s DFSUtil(s,visited) { // Create a stack for DFS let stack = []; // Push the current source node stack.push(s); while (stack.length != 0) { // Pop a vertex from stack and print it s = stack.pop(); // Stack may contain same vertex twice. So // we need to print the popped item only // if it is not visited. if (visited[s] == false ) { document.write(s + " " ); visited[s] = true ; } // Get all adjacent vertices of the popped vertex s // If a adjacent has not been visited, then push it // to the stack. for (let itr=0;itr< this .adj[s].length;itr++) { let v = this .adj[s][itr]; if (!visited[v]) stack.push(v); } } } // prints all vertices in DFS manner DFS() { let visited = [] // Mark all the vertices as not visited for (let i = 0; i < this .V; i++) visited.push( false ); for (let i = 0; i < this .V; i++) if (!visited[i]) this .DFSUtil(i, visited); } } // Driver program to test methods of graph class let g = new Graph(5); g.addEdge(1, 0); g.addEdge(2, 1); g.addEdge(3, 4); g.addEdge(4, 0); document.write( "Following is Depth First Traversal<br>" ); g.DFS(); // This code is contributed by avanitrachhadiya2155 </script> |
输出:
Following is Depth First Traversal0 1 2 3 4
与递归遍历一样,迭代实现的时间复杂度为O(V+E)。
本文由 希瓦姆 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



